上海教育版数学八上《勾股定理》同步练习 5页

19.9 勾股定理 一、课本巩固练习 1.在一直角三角形中有两边长分别是 3、4，则其第三边长为 2、已知直角三角形的两边长为 3、2，则另一条边长是________________． 3、在一个直角三角形中，若斜边长为 5cm，直角边的长为 3cm，则另一条直角边的长为_______________． 4、下面四组数中是勾股数的有（ ）． （1）1.5，2.5，2 （2） 2 ， 2 ，2 （3）12，16，20 （4）0.5，1.2，1.3 A．1 组 B．2 组 C．3 组 D．4 组 5、以下列各组数为边长，能组成直角三角形的是（ ） A．2，3，4 B．10，8，4 C．7，25，24 D．7，15，12 6、已知：在△ABC 中，∠A、∠B、∠C 的对边分别是 a、b、c，满足 a2+b2+c2+338=10a+24b+26c。 试判断△ABC 的形状。 7、若△ABC 的三边 a、b、c 满足 a2+b2+c2+50=6a+8b+10c，试判断△ABC 的形状。 8、已知：如图，已知∠B=∠D=90°，∠A=60°，AB=10，CD=6。 求：四边形 ABCD 的面积。 A B C D 9、已知，如图，四边形 ABCD 中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，且∠A=90°，则四 边形 ABCD 的面积 10.如图，矩形纸片 ABCD 的边 AB=10cm，BC=6cm，E 为 BC 上一点，将矩形纸片沿 AE 折叠，点 B 恰好落在 CD 边上的 点 G 处，求 BE 的长. 二、基础过关 1．已知△ABC 中，∠A= 1 2 ∠B= 1 3 ∠C，则它的三条边之比为（ ）． A．1：1： 2 B．1： 3 ：2 C．1： 2 ： 3 D．1：4：1 2．已知直角三角形一个锐角 60°，斜边长为 1，那么此直角三角形的周长是（ ）． A． 5 2 B．3 C． 3 2 2  D． 3 3 2  3．下列各组线段中，能够组成直角三角形的是（ ）． A．6，7，8 B．5，6，7 C．4，5，6 D．3，4，5 4．下列各命题的逆命题成立的是（ ） A．全等三角形的对应角相等 B．如果两个数相等，那么它们的绝对值相等 C．两直线平行，同位角相等 D．如果两个角都是 45°，那么这两个角相等 5．若等边△ABC 的边长为 2cm，那么△ABC 的面积为（ ）． A． 3 cm2 B．2 3 cm2 C．3 3 cm2 D．4cm2 6．在 Rt△ABC 中，已知其两直角边长 a=1，b=3，那么斜边 c 的长为（ ）． A．2 B．4 C．2 2 D． 10 7．如图所示，△ABC 中，CD⊥AB 于 D，若 AD=2BD，AC=5，BC=4，则 BD 的长为（ ）． A． 5 B． 3 C．1 D． 1 2 8．直角三角形有一条直角边长为 13，另外两条边长都是自然数，则周长为（ ） A．182 B．183 C．184 D．185 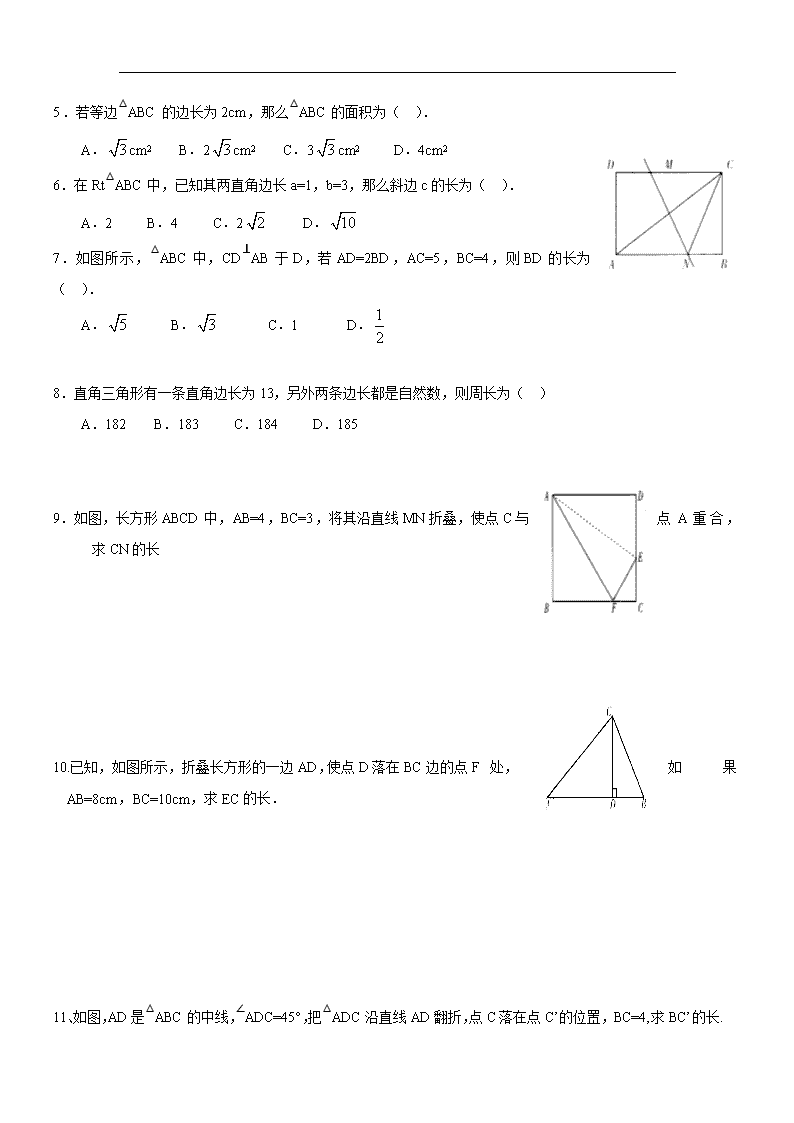9．如图，长方形 ABCD 中，AB=4，BC=3，将其沿直线 MN 折叠，使点 C 与 点 A 重合， 求 CN 的长 10.已知，如图所示，折叠长方形的一边 AD，使点 D 落在 BC 边的点 F处， 如 果 AB=8cm，BC=10cm，求 EC 的长． 11、如图，AD 是△ABC 的中线，∠ADC=45°，把△ADC 沿直线 AD 翻折，点 C 落在点 C’的位置，BC=4,求 BC’ 的长. 12、一只蚂蚁如果沿长方体的表面从 A 点爬到 B’点,那么沿哪条路最近,最短的路程是多少?已知长方体的长 2cm、 宽为 1cm、高为 4cm. 13、如图，一个梯子 AB=5 米，顶端 A 靠在墙 AC 上，这时梯子下端 B 与墙角 C 间的距离为 3m 梯子滑动后停在 DE 位置上，如图，测得 DB 的长为 1m，则梯子顶端 A 下落了多少 m? 14、在 ABC 中, 1AB AC  , BC 边上有 2006 个不同的点 1 2 2006, ,P P P , 记  2 1,2, 2006i i i im AP BP PC i     ,则 1 2 2006m m m  =_____. .15、细心观察下图，认真分析各式，然后解答问题． （ 1 ）2+1=2 S1= 1 2 （ 2 ）2+1=3 S2= 2 2 （ 3 ）2+4=5 S3= 3 2 Dˊ A B C D Aˊ Bˊ Cˊ （1）请用含 n（n 是正整数）的等式表示上述变化规律； （2）推算出 OA10 的长； 求出 S12+S22+S22+…+S102 的值