青岛版第1章全等三角形测试卷 19页

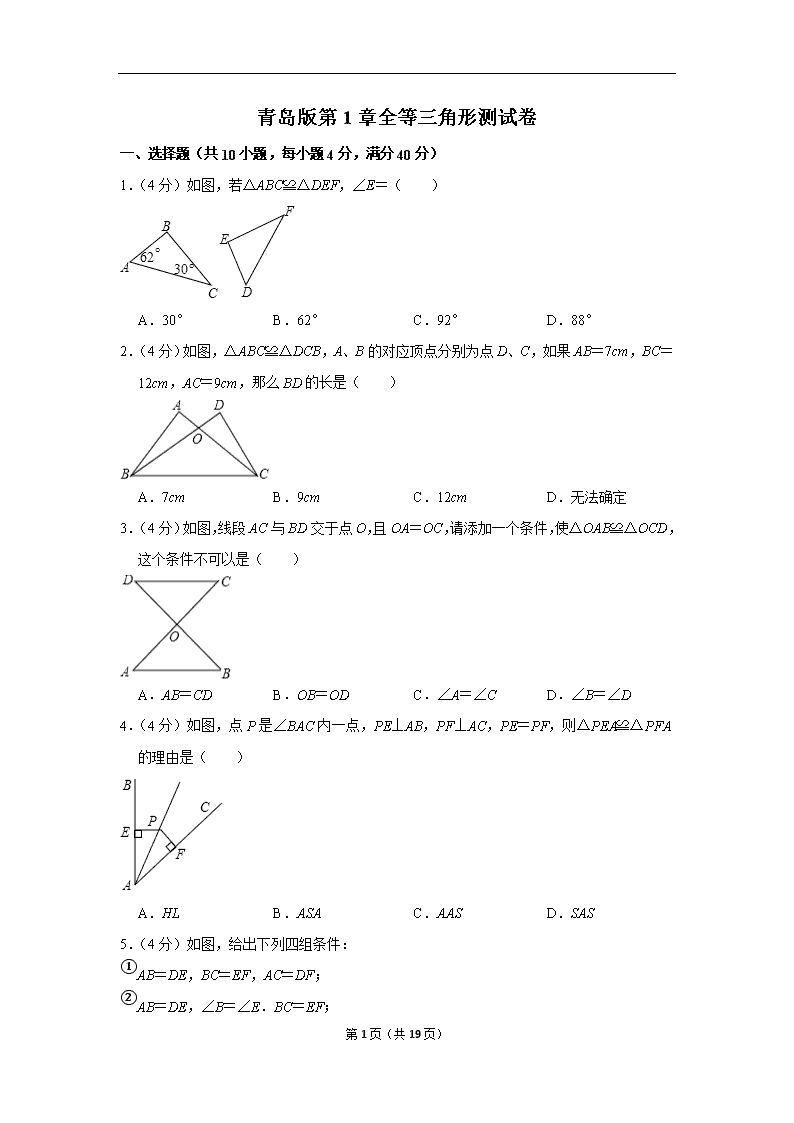
第 1页（共 19页） 青岛版第 1 章全等三角形测试卷 一、选择题（共 10 小题，每小题 4 分，满分 40 分） 1．（4 分）如图，若△ABC≌△DEF，∠E＝（ ） A．30° B．62° C．92° D．88° 2．（4 分）如图，△ABC≌△DCB，A、B 的对应顶点分别为点 D、C，如果 AB＝7cm，BC ＝12cm，AC＝9cm，那么 BD 的长是（ ） A．7cm B．9cm C．12cm D．无法确定 3．（4 分）如图，线段 AC 与 BD 交于点 O，且 OA＝OC，请添加一个条件，使△OAB≌△ OCD，这个条件不可以是（ ） A．AB＝CD B．OB＝OD C．∠A＝∠C D．∠B＝∠D 4．（4 分）如图，点 P 是∠BAC 内一点，PE⊥AB，PF⊥AC，PE＝PF，则△PEA≌△PFA 的理由是（ ） A．HL B．ASA C．AAS D．SAS 5．（4 分）如图，给出下列四组条件： ① AB＝DE，BC＝EF，AC＝DF； ② AB＝DE，∠B＝∠E．BC＝EF； 第 2页（共 19页） ③ ∠B＝∠E，BC＝EF，∠C＝∠F； ④ AB＝DE，AC＝DF，∠B＝∠E． 其中，能使△ABC≌△DEF 的条件共有（ ） A．1 组 B．2 组 C．3 组 D．4 组 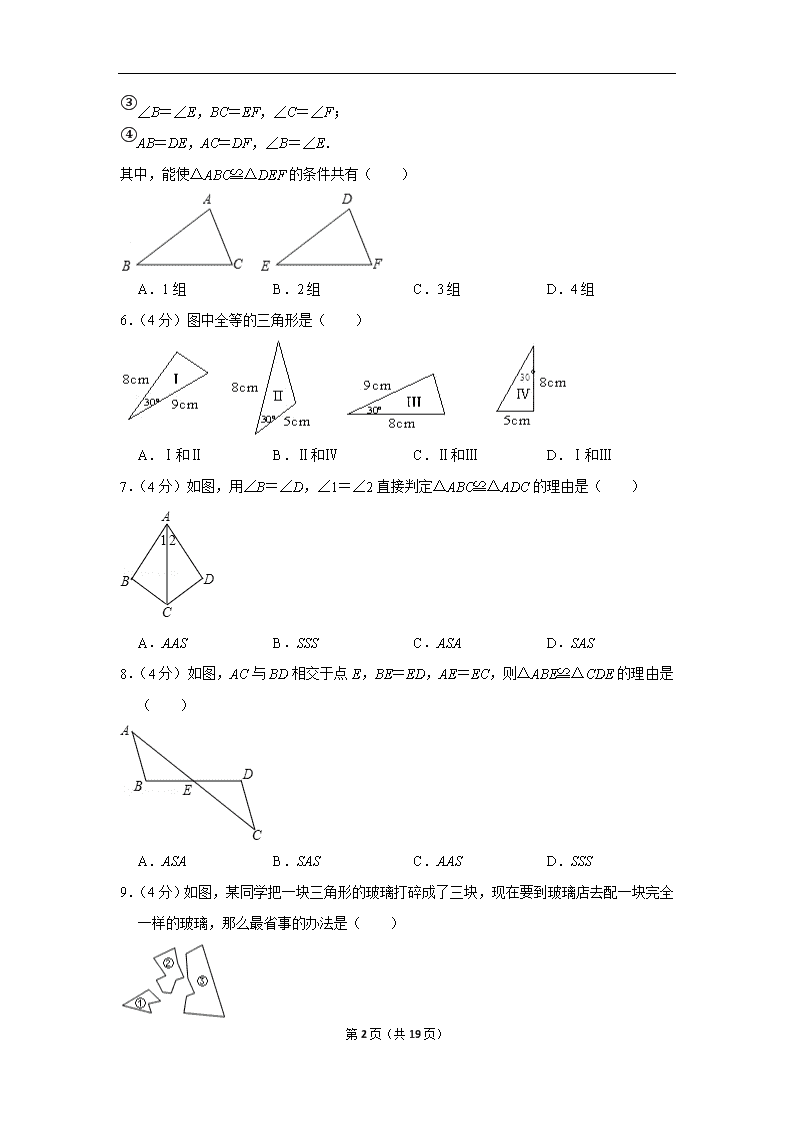6．（4 分）图中全等的三角形是（ ） A．Ⅰ和Ⅱ B．Ⅱ和Ⅳ C．Ⅱ和Ⅲ D．Ⅰ和Ⅲ 7．（4 分）如图，用∠B＝∠D，∠1＝∠2 直接判定△ABC≌△ADC 的理由是（ ） A．AAS B．SSS C．ASA D．SAS 8．（4 分）如图，AC 与 BD 相交于点 E，BE＝ED，AE＝EC，则△ABE≌△CDE 的理由是 （ ） A．ASA B．SAS C．AAS D．SSS 9．（4 分）如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全 一样的玻璃，那么最省事的办法是（ ） 第 3页（共 19页） A．带 ① 去 B．带 ② 去 C．带 ③ 去 D．带 ① 和 ② 去 10．（4 分）已知：如图，CD⊥AB，BE⊥AC，垂足分别为 D、E，BE、CD 相交于 O 点，∠ 1＝∠2．图中全等的三角形共有（ ） A．4 对 B．3 对 C．2 对 D．1 对 二、填空题（共 6 小题，每小题 4 分，满分 24 分） 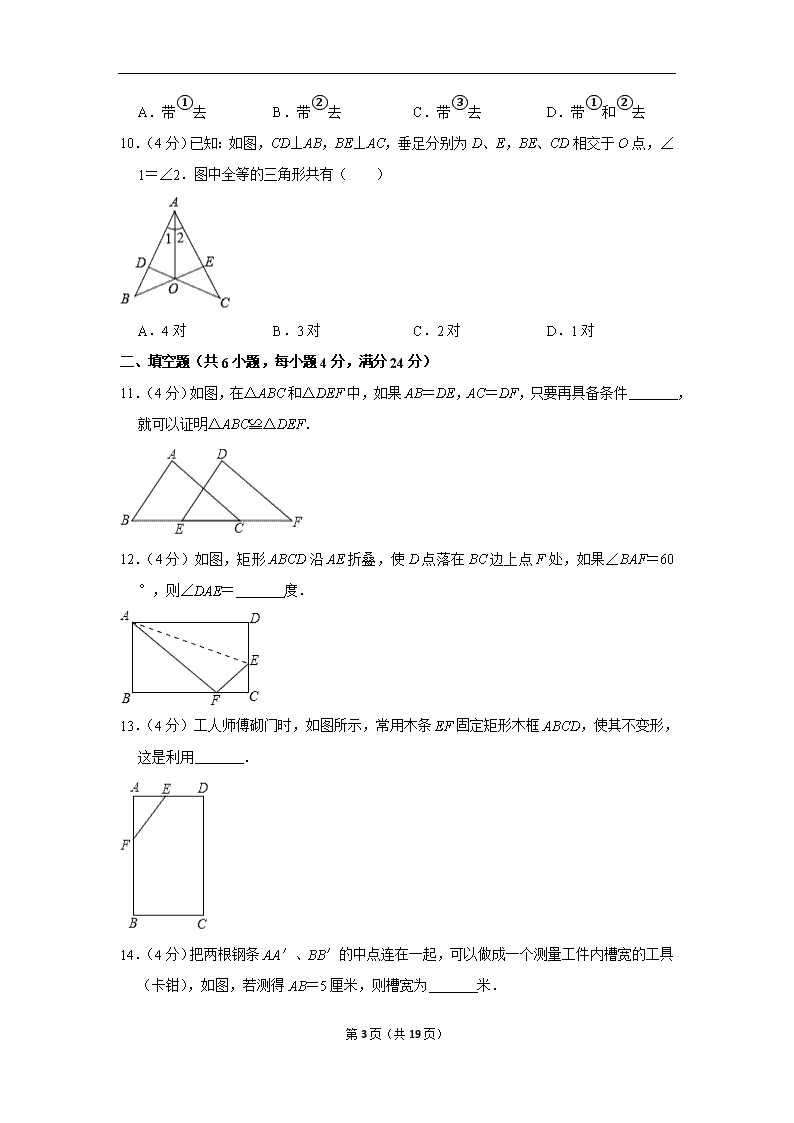11．（4 分）如图，在△ABC 和△DEF 中，如果 AB＝DE，AC＝DF，只要再具备条件 ， 就可以证明△ABC≌△DEF． 12．（4 分）如图，矩形 ABCD 沿 AE 折叠，使 D 点落在 BC 边上点 F 处，如果∠BAF＝60°， 则∠DAE＝ 度． 13．（4 分）工人师傅砌门时，如图所示，常用木条 EF 固定矩形木框 ABCD，使其不变形， 这是利用 ． 14．（4 分）把两根钢条 AA′、BB′的中点连在一起，可以做成一个测量工件内槽宽的工具 （卡钳），如图，若测得 AB＝5 厘米，则槽宽为 米． 第 4页（共 19页） 15．（4 分）如图，四边形 ABCD 的对角线相交于 O 点，且有 AB∥DC，AD∥BC，则图中有 对全等三角形． 16．（4 分）如图，已知等边△ABC 中，BD＝CE，AD 与 BE 相交于点 P，则∠APE 的度数 是 度． 三、解答题（共 4 小题，满分 36 分） 17．（8 分）如图：△ABC 和△DBC 的顶点 A 和 D 在 BC 的同旁，AB＝DC，AC＝DB，AC 和 DB 相交于点 O，求证：∠A＝∠D． 18．（9 分）如图，CD＝CA，∠1＝∠2，EC＝BC，与 DE 相等的线段是哪一条？说明理由． 19．（9 分）如图，点 B、C、E、F 在同一直线上，AB∥DE，∠A＝∠D，BF＝CE 求证：AB＝DE． 第 5页（共 19页） 20．（10 分）如图所示，已知线段 a、b、h（h＜b）．求作△ABC，使 BC＝a，AB＝b，BC 边上的高 AD＝h．（要求：写出作法，并保留作图痕迹） 答案 一、选择题（共 10 小题，每小题 4 分，满分 40 分） 第 6页（共 19页） 1．（4 分）如图，若△ABC≌△DEF，∠E＝（ ） A．30° B．62° C．92° D．88° 【考点】KA：全等三角形的性质． 【分析】先根据三角形内角和等于 180°求出∠B 的度数，再根据全等三角形的对应角相等 得出∠E＝∠B． 【解答】解：△ABC 中，∵∠A＝62°，∠C＝30°， ∴∠B＝180°﹣∠A﹣∠C＝180°﹣62°﹣30°＝88°， ∵△ABC≌△DEF， ∴∠B＝∠E＝88°． 故选：D． 【点评】本题考查了全等三角形的性质；解答时，除必备的知识外，还应将条件和所求联系 起来，即将所求的角与已知角通过全等及三角形内角之间的关系联系起来． 2．（4 分）如图，△ABC≌△DCB，A、B 的对应顶点分别为点 D、C，如果 AB＝7cm，BC ＝12cm，AC＝9cm，那么 BD 的长是（ ） A．7cm B．9cm C．12cm D．无法确定 【考点】KA：全等三角形的性质． 【分析】由△ABC≌△DCB，A、B 的对应顶点分别为点 D、C，根据全等三角形的对应边相 等，即可得 BD＝CA，又由 AC＝9cm，即可求得 BD 的长． 【解答】解：∵△ABC≌△DCB，A、B 的对应顶点分别为点 D、C， ∴BD＝CA， ∵AC＝9cm， ∴BD＝9cm． 故选：B． 【点评】此题考查了全等三角形的性质．此题比较简单，解题的关键是注意掌握全等三角形 第 7页（共 19页） 的对应边相等，注意对应关系． 3．（4 分）如图，线段 AC 与 BD 交于点 O，且 OA＝OC，请添加一个条件，使△OAB≌△ OCD，这个条件不可以是（ ） A．AB＝CD B．OB＝OD C．∠A＝∠C D．∠B＝∠D 【考点】KB：全等三角形的判定． 【分析】由于 OA＝OC，加上对顶角相等得∠AOB＝∠COD，然后分别添加四个选项中的条 件，利用全等三角形的判定方法分别进行判断． 【解答】解：∵OA＝OC， 而∠AOB＝∠COD， ∴当 AB＝CD 时，不能判断△OAB≌△OCD； 当 OB＝OD 时，可根据“SAS”判断△OAB≌△OCD； 当∠A＝∠C 时，可根据“ASA”判断△OAB≌△OCD； 当∠B＝∠D 时，可根据“AAS”判断△OAB≌△OCD． 故选：A． 【点评】本题考查了全等三角形的判定：全等三角形的 5 种判定方法中，选用哪一种方法， 取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两 角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则 找另一组角，或找这个角的另一组对应邻边． 4．（4 分）如图，点 P 是∠BAC 内一点，PE⊥AB，PF⊥AC，PE＝PF，则△PEA≌△PFA 的理由是（ ） A．HL B．ASA C．AAS D．SAS 【考点】KB：全等三角形的判定． 第 8页（共 19页） 【分析】根据角平分线的性质可得 P 在∠BAC 的角平分线上，可得∠EAP＝∠FAP，再加上 条件∠PEA＝∠PFA＝90°和公共边 AP＝AP 可根据 AAS 证明△PEA≌PFA． 【解答】解：∵PE⊥AB，PF⊥AC，PE＝PF， ∴P 在∠BAC 的角平分线上，∠PEA＝∠PFA＝90°， ∴∠EAP＝∠FAP， 在△EAP 和△FAP 中 ， ∴△EAP≌△FAP（AAS）， 故选：C． 【点评】此题主要考查了三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、 SAS、ASA、AAS、HL． 注意：AAA、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若 有两边一角对应相等时，角必须是两边的夹角． 5．（4 分）如图，给出下列四组条件： ① AB＝DE，BC＝EF，AC＝DF； ② AB＝DE，∠B＝∠E．BC＝EF； ③ ∠B＝∠E，BC＝EF，∠C＝∠F； ④ AB＝DE，AC＝DF，∠B＝∠E． 其中，能使△ABC≌△DEF 的条件共有（ ） A．1 组 B．2 组 C．3 组 D．4 组 【考点】KB：全等三角形的判定． 【分析】要使△ABC≌△DEF 的条件必须满足 SSS、SAS、ASA、AAS，可据此进行判断． 【解答】解：第 ① 组满足 SSS，能证明△ABC≌△DEF． 第 ② 组满足 SAS，能证明△ABC≌△DEF． 第 ③ 组满足 ASA，能证明△ABC≌△DEF． 第 ④ 组只是 SSA，不能证明△ABC≌△DEF． 第 9页（共 19页） 所以有 3 组能证明△ABC≌△DEF． 故符合条件的有 3 组． 故选：C． 【点评】本题考查三角形全等的判定方法；判定两个三角形全等的一般方法有：SSS、SAS、 ASA、AAS、HL．添加时注意：AAA、SSA 不能判定两个三角形全等，不能添加，根据已 知结合图形及判定方法选择条件是正确解答本题的关键． 6．（4 分）图中全等的三角形是（ ） A．Ⅰ和Ⅱ B．Ⅱ和Ⅳ C．Ⅱ和Ⅲ D．Ⅰ和Ⅲ 【考点】KB：全等三角形的判定． 【分析】仔细观察图形，验证各选项给出的条件是否符合全等的判定方法，符合的是全等的 不符合的则不全等，题目中 D 选项的两个三角形符合 SAS，是全等的三角形，其它的都 不能得到三角形全等． 【解答】解：A 选项中条件不满足 SAS，不能判定两三角形全等； B 选项中条件对应边不相等，不能判定两三角形全等； C 选项中条件不满足 SAS，不能判定两三角形全等； D 选项中条件满足 SAS，能判定两三角形全等． 故选：D． 【点评】本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即 AAS、ASA、SAS、SSS，直角三角形可用 HL 定理．做题时要根据已知条件结合图形利用 全等的判定方法逐个寻找． 7．（4 分）如图，用∠B＝∠D，∠1＝∠2 直接判定△ABC≌△ADC 的理由是（ ） A．AAS B．SSS C．ASA D．SAS 第 10页（共 19页） 【考点】KB：全等三角形的判定． 【分析】由于∠B＝∠D，∠1＝∠2，再加上公共边，则可根据“AAS”判断△ABC≌△ADC． 【解答】解：在△ABC 和△ADC 中， ， ∴△ABC≌△ADC（AAS）． 故选：A． 【点评】本题考查了全等三角形的判定：全等三角形的 5 种判定方法中，选用哪一种方法， 取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两 角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则 找另一组角，或找这个角的另一组对应邻边． 8．（4 分）如图，AC 与 BD 相交于点 E，BE＝ED，AE＝EC，则△ABE≌△CDE 的理由是 （ ） A．ASA B．SAS C．AAS D．SSS 【考点】KB：全等三角形的判定． 【专题】11：计算题． 【分析】由于 BE＝ED，AE＝EC，再加上对顶角相等，则可根据“SAS”判断△ABE≌△CDE． 【解答】解：在△ABE 和△CDE 中， ， ∴△ABE≌△CDE（SAS）． 故选：B． 【点评】本题考查了全等三角形的判定：全等三角形的 5 种判定方法中，选用哪一种方法， 取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两 角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则 找另一组角，或找这个角的另一组对应邻边． 第 11页（共 19页） 9．（4 分）如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全 一样的玻璃，那么最省事的办法是（ ） A．带 ① 去 B．带 ② 去 C．带 ③ 去 D．带 ① 和 ② 去 【考点】KE：全等三角形的应用． 【专题】12：应用题． 【分析】此题可以采用全等三角形的判定方法以及排除法进行分析，从而确定最后的答案． 【解答】解：A、带 ① 去，仅保留了原三角形的一个角和部分边，不能得到与原来一样的三 角形，故 A 选项错误； B、带 ② 去，仅保留了原三角形的一部分边，也是不能得到与原来一样的三角形，故 B 选项 错误； C、带 ③ 去，不但保留了原三角形的两个角还保留了其中一个边，符合 ASA 判定，故 C 选 项正确； D、带 ① 和 ② 去，仅保留了原三角形的一个角和部分边，同样不能得到与原来一样的三角 形，故 D 选项错误． 故选：C． 【点评】主要考查学生对全等三角形的判定方法的灵活运用，要求对常用的几种方法熟练掌 握． 10．（4 分）已知：如图，CD⊥AB，BE⊥AC，垂足分别为 D、E，BE、CD 相交于 O 点，∠ 1＝∠2．图中全等的三角形共有（ ） A．4 对 B．3 对 C．2 对 D．1 对 【考点】KB：全等三角形的判定． 【分析】解此题的关键是三角形全等的判定定理的准确应用．三角形全等的判定定理有：SSS， SAS，ASA，AAS．做题时要从已知入手由易到难，不重不漏． 第 12页（共 19页） 【解答】解：∵CD⊥AB，BE⊥AC， ∴∠ADO＝∠AEO＝90°； ∵∠1＝∠2，AO＝AO， ∴△ADO≌△AEO（AAS）． ∴AD＝AE， ∵∠DAC＝∠EAB，∠ADO＝∠AEO， ∴△ADC≌△AEB（ASA）． ∴AB＝AC， ∵∠1＝∠2，AO＝AO， ∴△AOB≌△AOC（SAS）． ∴∠B＝∠C， ∵AD＝AE，AB＝AC， ∴DB＝EC； ∵∠BOD＝∠COE， ∴△BOD≌△COE（AAS）． 故选：A． 【点评】此题考查了三角形全等的判定与性质，解题的关键是要注意正确识图． 二、填空题（共 6 小题，每小题 4 分，满分 24 分） 11．（4 分）如图，在△ABC 和△DEF 中，如果 AB＝DE，AC＝DF，只要再具备条件 BC ＝EF 或∠A＝∠D ，就可以证明△ABC≌△DEF． 【考点】KB：全等三角形的判定． 【专题】26：开放型． 【分析】根据“SSS”判断△ABC≌△DEF，则需添加 BC＝EF；根据“SAS”判断△ABC≌ △DEF，则需添加∠A＝∠D． 【解答】解：∵AB＝DE，AC＝DF， ∴当 BC＝EF 时，可根据“SSS”判断△ABC≌△DEF； 第 13页（共 19页） 当∠A＝∠D 时，可根据“SAS”判断△ABC≌△DEF． 故答案为 BC＝EF 或∠A＝∠D． 【点评】本题考查了全等三角形的判定：全等三角形的 5 种判定方法中，选用哪一种方法， 取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两 角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则 找另一组角，或找这个角的另一组对应邻边． 12．（4 分）如图，矩形 ABCD 沿 AE 折叠，使 D 点落在 BC 边上点 F 处，如果∠BAF＝60°， 则∠DAE＝ 15 度． 【考点】LB：矩形的性质；PB：翻折变换（折叠问题）． 【专题】16：压轴题． 【分析】先求得∠DAF＝30°，又根据 AF 是 AD 折叠得到的（翻折前后的对应角相等），可 知∠DAE＝∠EAF＝15°． 【解答】解：∵∠BAF＝60°， ∴∠DAF＝30°， 又∵AF 是 AD 折叠得到的， ∴△ADE≌△AFE， ∴∠DAE＝∠EAF＝ ∠DAF＝15°． 故答案为 15． 【点评】此题主要考查学生对翻折变换及矩形的性质的掌握情况． 13．（4 分）工人师傅砌门时，如图所示，常用木条 EF 固定矩形木框 ABCD，使其不变形， 这是利用 三角形的稳定性 ． 第 14页（共 19页） 【考点】K4：三角形的稳定性． 【分析】三角形具有稳定性，其它多边形不具有稳定性，把多边形分割成三角形则多边形的 形状就不会改变． 【解答】解：这是利用三角形的稳定性． 【点评】本题考查三角形稳定性的实际应用，三角形的稳定性在实际生活中有着广泛的应用， 如钢架桥、房屋架梁等，因此要使一些图形具有稳定的结构，往往通过连接辅助线转化 为三角形而获得． 14．（4 分）把两根钢条 AA′、BB′的中点连在一起，可以做成一个测量工件内槽宽的工具 （卡钳），如图，若测得 AB＝5 厘米，则槽宽为 0.05 米． 【考点】KE：全等三角形的应用． 【专题】11：计算题． 【分析】连接 AB，A′B′，根据 O 为 AB′和 BA′的中点，且∠A′OB′＝∠AOB 即可判 定△OA′B′≌△OAB，即可求得 A′B′的长度． 【解答】解：连接 AB，A′B′， O 为 AB′和 BA′的中点， ∴OA′＝OB，OA＝OB′， ∵∠A′OB′＝∠AOB ∴△OA′B′≌△OAB， 即 A′B′＝AB， 故 A′B′＝5cm， 5cm＝0.05m． 故答案为 0.05． 第 15页（共 19页） 【点评】本题考查了全等三角形在实际生活中的应用，考查了全等三角形的证明和对应边相 等的性质，本题中求证△OA′B′≌△OAB 是解题的关键． 15．（4 分）如图，四边形 ABCD 的对角线相交于 O 点，且有 AB∥DC，AD∥BC，则图中有 4 对全等三角形． 【考点】L6：平行四边形的判定． 【分析】根据平行四边形判定方法可以判定四边形 ABCD 是平行四边形，根据平行四边形 性质可得两组对边相等，两组对角相等，对角线互相平分；可得出共有四对全等三角形． 【解答】解：∵AB∥DC，AD∥BC， ∴四边形 ABCD 是平行四边形， ∴AB＝CD，AD＝BC，OA＝OC，OB＝OD，∠ABC＝∠ADC，∠BAD＝∠BCD， ∴△ABC≌△ADC，△BAD≌△BCD； ∵∠AOB＝∠COD，∠AOD＝∠BOC， ∴△AOB≌△COD，△AOD≌△COD． ∴图中有四对全等三角形． 故答案为：4． 【点评】本题主要考查全等三角形的判定和平行四边形的性质．常用的全等三角形的判定方 法有：SSS、SAS、AAS、ASA、HL．需要注意的是 AAA 和 SSA 不能判定两个三角形全等． 16．（4 分）如图，已知等边△ABC 中，BD＝CE，AD 与 BE 相交于点 P，则∠APE 的度数 是 60 度． 第 16页（共 19页） 【考点】KD：全等三角形的判定与性质；KK：等边三角形的性质． 【专题】121：几何图形问题． 【分析】根据题目已知条件可证△ABD≌△BCE，再利用全等三角形的性质及三角形外角和 定理求解． 【解答】解：∵等边△ABC， ∴∠ABD＝∠C，AB＝BC， 在△ABD 与△BCE 中， ， ∴△ABD≌△BCE（SAS）， ∴∠BAD＝∠CBE， ∵∠ABE+∠EBC＝60°， ∴∠ABE+∠BAD＝60°， ∴∠APE＝∠ABE+∠BAD＝60°， ∴∠APE＝60°． 故答案为：60． 【点评】本题利用等边三角形的性质来为三角形全等的判定创造条件，是中考的热点． 三、解答题（共 4 小题，满分 36 分） 17．（8 分）如图：△ABC 和△DBC 的顶点 A 和 D 在 BC 的同旁，AB＝DC，AC＝DB，AC 和 DB 相交于点 O，求证：∠A＝∠D． 第 17页（共 19页） 【考点】KD：全等三角形的判定与性质． 【专题】14：证明题． 【分析】由△ABC 和△DBC 的顶点 A 和 D 在 BC 的同旁，AB＝DC，AC＝DB，利用 SSS， 即可判定△ABC≌△DCB，继而证得：∠A＝∠D． 【解答】证明：在△ABC 和△DCB 中， ， ∴△ABC≌△DCB（SSS）， ∴∠A＝∠D． 【点评】此题考查了全等三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应 用． 18．（9 分）如图，CD＝CA，∠1＝∠2，EC＝BC，与 DE 相等的线段是哪一条？说明理由． 【考点】KD：全等三角形的判定与性质． 【专题】1：常规题型． 【分析】先利用∠1＝∠2 得到∠ACB＝∠DCE，然后根据“SAS”证明△ACB≌△DCE，则 根据全等三角形的性质得 DE＝AB． 【解答】解：DE＝AB．理由如下： ∵∠1＝∠2， ∴∠1+ACE＝∠2+∠ACE， 即∠ACB＝∠DCE， 在△ABC 和△DCE 中， 第 18页（共 19页） ， ∴△ACB≌△DCE（SAS）， ∴AB＝DE． 【点评】本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质 证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件． 19．（9 分）如图，点 B、C、E、F 在同一直线上，AB∥DE，∠A＝∠D，BF＝CE 求证：AB＝DE． 【考点】KD：全等三角形的判定与性质． 【专题】14：证明题． 【分析】由 AB∥DE，BF＝CE，易得∠B＝∠E，BC＝EF，然后利用 SAS 即可判定△ABC ≌△DEF，继而证得 AB＝DE． 【解答】证明：∵AB∥DE，BF＝CE， ∴∠B＝∠E，BC＝EF， 在△ABC 和△DEF 中， ， ∴△ABC≌△DEF（AAS）， ∴AB＝DE． 【点评】此题考查了全等三角形的判定与性质．此题难度不大，注意掌握数形结合思想的应 用． 20．（10 分）如图所示，已知线段 a、b、h（h＜b）．求作△ABC，使 BC＝a，AB＝b，BC 边上的高 AD＝h．（要求：写出作法，并保留作图痕迹） 第 19页（共 19页） 【考点】N3：作图—复杂作图． 【分析】根据基本尺规作图的方法，作出不同情况的三角形即可． 【解答】解：1、作直线 PQ，在直线 PQ 上任取一点 D，作 DM⊥PQ； 2、在 DM 上截取线段 DA＝h； 3、以 A 为圆心，b 为半径画弧交射线 DP 于 B； 4、以 B 为圆心，a 为半径画弧，分别交射线 BP 和射线 BQ 于 C1 和 C2； 5、连接 AC1、AC2， 则△ABC1（或 ABC2）即为所求． 【点评】本题考查的是复杂的尺规作图，掌握基本尺规作图是解题的关键，解答时，要从不 同角度即锐角三角形和钝角三角形考虑问题．