人教版八年级下册数学试题课件-1第十八章18平行四边形的性质（一） 26页

中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 第十八章 平行四边形 18.1 平行四边形 第1课时 平行四边形的性质（一） 课前预习 A. 平行四边形的定义：两组对边分别_ __的四边形叫做平行四边形. 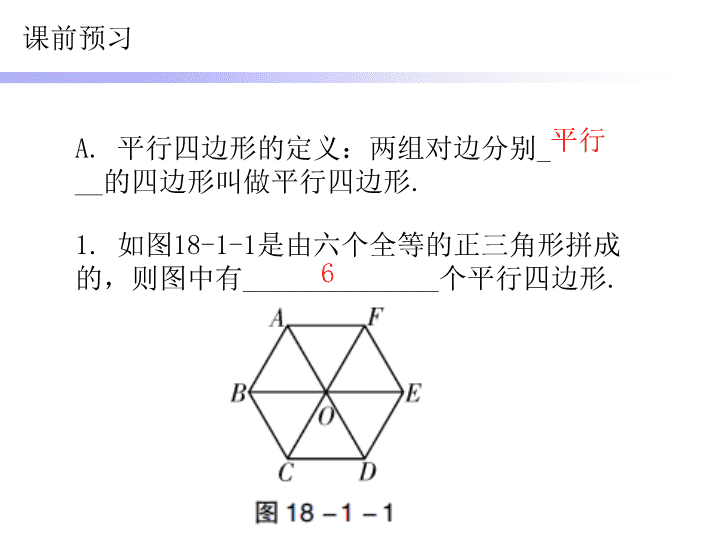1. 如图18-1-1是由六个全等的正三角形拼成 的，则图中有______________个平行四边形. 6 平行 B. 平行四边形的性质：平行四边形的对边 ______________，对角_____________. 相等 相等 2. 如图18-1-2，将 ABCD的一边BC延长至点E，若 ∠A=110°，则∠1=__________. 70° 课堂讲练 知识点1 平行四边形的定义 【例1】如图18-1-3，在 ABCD中，EF∥AB，GH∥AD， 则图中有多少个平行四边形？ 解:∵在□ABCD中，EF∥AB，GH∥AD， ∴EF∥AB∥CD，GH∥AD∥BC. 故除□ABCD外，图中还有□AGOE，□AGHD， □ABFE，□GBFO，□GBCH， □FCHO，□FCDE，□HDEO，共9个平行四边形. 1. 如图18-1-4，△DEF是等边三角形ABC沿线段 BC方向平移得到的，请你想一想，图中共有多 少个等边三角形？多少个平行四边形？ 解：∵△DEF是等边三角形 ABC沿线段BC方向平移得到， ∴∠DEF=∠F=∠EDF=60°. ∴图中等边三角形有△ABC， △DEF，△ADG，△CEG共4个. 平行四边形有□ADEB， □ADFC共2个. 知识点2 平行四边形的性质 【例2】如图18-1-5，BD是□ABCD的对角线，AE⊥BD， CF⊥BD，垂足分别为点E，F. 求证：AE=CF. 解：∵四边形ABCD是平行 四边形， ∴AB=CD，AB∥CD. ∴∠ABE=∠CDF. ∵AE⊥BD，CF⊥BD， ∴∠AEB=∠CFD=90°. ∴△ABE≌△CDF（AAS）. ∴AE=CF. 2. 如图18-1-6，在平行四边形ABCD中，AB=2AD，M 为AB的中点，连接DM,MC，试问直线DM和MC有何位 置关系？请证明. 解：DM与MC互相垂直.证明如下. ∵M是AB的中点，∴AB=2AM. 又∵AB=2AD，∴AM=AD.∴∠ADM=∠AMD. ∵四边形ABCD是平行四边形，∴AB∥CD. ∴∠AMD=∠MDC. ∴∠ADM=∠MDC，即∠MDC= ∠ADC. 同理∠MCD= ∠BCD. ∵AD∥BC，∴∠ADC+∠DCB=180°. ∴∠MDC+∠MCD= ∠ADC+ ∠BCD=90°. ∵∠MDC+∠MCD+∠DMC=180°， ∴∠DMC=90°. ∴DM与MC互相垂直. 分层训练 【A组】 1. 如图18-1-7，平行四边形ABCD中，BD⊥AD， ∠A=30°，BD=4，则CD的长为（ ） A. 2 B. 4 C. 4 D. 8 D 2. 在□ABCD中，∠A∶∠B∶∠C∶∠D的值 可以是（ ） A. 1∶2∶3∶4 B. 1∶2∶2∶1 C. 2∶2∶1∶1 D. 2∶1∶2∶1 D 3. 平行四边形的一个内角为50°，它的相邻 的一个内角等于（ ） A. 40°B. 50°C. 130°D. 150° C 4. 如图18-1-8，在□ABCD中，AD=7，CE平分 ∠BCD交AD边于点E，且AE=3，则AB的长为（ ） A. 4 B. 3 C. D. 2 A 5. 如图18-1-9，在□ABCD中，EF∥BC，则图中平 行四边形有__________个. 3 6. 在□ABCD中，若∠A∶∠B=1∶5，则∠D=_______； 若∠A+∠C=140°，则∠D=_______. 7. 如图18-1-10，在□ABCD中，AE,AF分别垂直于 BC,DC的延长线，垂足为E,F，若∠EAF=30°，AB=6， AD=10，则CD=______,AB与CD的距离为______,AD与 BC的距离为______,∠D=______. 150° 110° 6 5 3 30° 8. 如图18-1-11，在 ABCD中，CE平分∠BCD， 且交AD于点E，AF∥CE，且交BC于点F. （1）求证：△ABF≌△CDE； （2）若∠B=52°，求∠1的大小. □ （1）证明：∵四边形ABCD是平行四边形, ∴AB=CD,∠B=∠D,AD∥BC. ∴∠1=∠ECB. ∵AF∥CE，∴∠AFB=∠ECB. ∴∠1=∠AFB. 又∵∠B=∠D，AB=CD， ∴△ABF≌△CDE（AAS）. （2）∵CE平分∠BCD，∴∠ECB=∠ECD. ∵∠1=∠ECB（已证），∴∠1=∠ECD. ∵∠B=52°，∴∠D=∠B=52°. ∴∠1=∠ECD= ×（180°-52°）=64°. 9. 如图18-1-12，在 ABCD中，从顶点D向 AB作垂线，垂足为点E，且E是AB的中点，已 知 ABCD的周长为8.6 cm，△ABD的周长为 6 cm，求AB,BC的长． 【B组】 □ □ 解：由已知可推出AD=BD=BC． 设BC=x cm，AB=y cm， 则 解得 即AB长2.6 cm，BC长1.7 cm． 10. 如图18-1-13，四边形ABCD是平行四边形， 点E，A，C，F在同一直线上，且AE=CF.求证： BE=DF. 证明：∵四边形ABCD为平行四边形， ∴BC=AD，BC∥AD. ∴∠BCA=∠DAC. 又∵AE=CF， ∴EC=AF. 在△BCE和△DAF中， ∴△BCE≌△DAF（SAS）. ∴BE=DF. 11. 如图18-1-14，四边形ABCD是平行四边形，P是 CD上一点，且AP和BP分别平分∠DAB和∠CBA. （1）求∠APB的度数； （2）如果AD＝5 cm，AP＝8 cm，求△APB的周长. 解：（1）∵四边形ABCD是平行四边形， ∴AD∥CB，AB∥CD. ∴∠DAB＋∠CBA＝180°. 又∵AP和BP分别平分∠DAB和∠CBA， ∴∠PAB＋∠PBA＝ （∠DAB＋∠CBA）＝90°. ∴∠APB＝180°－（∠PAB＋∠PBA）＝90°. （2）∵AP平分∠DAB且AB∥CD， ∴∠DAP＝∠PAB＝∠DPA. ∴△ADP是等腰三角形. ∴AD＝DP＝5 cm. 同理PC＝CB＝5 cm. ∴AB＝CD＝DP＋PC＝10 cm. 在Rt△APB中，AB＝10 cm，AP＝8 cm， ∴BP＝ ＝6 （cm）. ∴△APB的周长是6＋8＋10＝24 （cm）. 【C组】 12. 如图18-1-15，在 ABCD中，CG⊥AB于点 G，∠ABF=45°，点F在CD上，BF交CG于点E， 连接AE，且AE⊥AD. （1）若BG=2，BC= ，求EF的长度； （2）求证：CE+ BE=AB. □ 解：（1）∵CG⊥AB， ∴∠AGC=∠CGB=90°. ∵BG=2，BC= ， ∴CG= =5. ∵∠ABF=45°，∴BG=EG=2， ∴CE=CG-EG=3. ∵四边形ABCD是平行四边形，∴AB∥CD， ∴∠GCD=∠BGC=90°，∠EFC=∠GBE=45°， ∴CF=CE=3，∴EF= . （2）证明：如答图18-1-1，延长AE交BC于点H， ∵四边形ABCD是平行四边形， ∴BC∥AD，∴∠AHB=∠HAD， ∵AE⊥AD，∴∠AHB=∠HAD=90°， ∴∠BAH+∠ABH=∠BCG+∠CBG=90°， ∴∠GAE=∠GCB， 在△BCG与△EAG中， ∴△BCG≌△EAG（AAS）. ∴AG=CG. ∴AB=BG+AG=CE+EG+BG. ∵BG=EG= BE， ∴CE+ BE=AB.