八年级下册数学同步练习2-6-2 菱形的判定3 湘教版 7页

‎2.6.2 菱形的判定 要点感知1 四条边__________的四边形是菱形.‎ 预习练习1-1 用直尺和圆规作一个菱形，如图，能得到四边形ABCD是菱形的依据是( )‎ ‎ A.一组临边相等的四边形是菱形 ‎ B.四边相等的四边形是菱形 ‎ C.对角线互相垂直的平行四边形是菱形 ‎ D.每条对角线平分一组对角的平行四边形是菱形 ‎ ‎ ‎ 图1-1 图2-1‎ 要点感知2 对角线__________的平行四边形是菱形.‎ 预习练习2-1 如图，四边形ABCD的对角线AC，BD互相垂直，则下列条件能判定四边形ABCD为菱形的条件是( )‎ ‎ A.BA=BC B.AC，BD互相平分 C.AC=BD D.AB∥CD 知识点1 四条边都相等的四边形是菱形 ‎1.如图，四边形ABCD内有一点E，AE=BE=DE=BC=DC，AB=AD，若∠C=100°，则∠AED的大小是( )‎ ‎ A.120° B.130° C.140° D.150°‎ ‎2.顺次连接矩形四边中点所形成的四边形是__________，学校的一块菱形花圃两对角线的长分别是6 m和8 m，则这个花圃的面积为__________.‎ ‎3.如图，在四边形ABCD中，E，F，G，H分别是AB，BD，CD，AC的中点，AD=BC，求证：四边形EFGH是菱形.‎ 知识点2 对角线互相垂直的平行四边形是菱形 ‎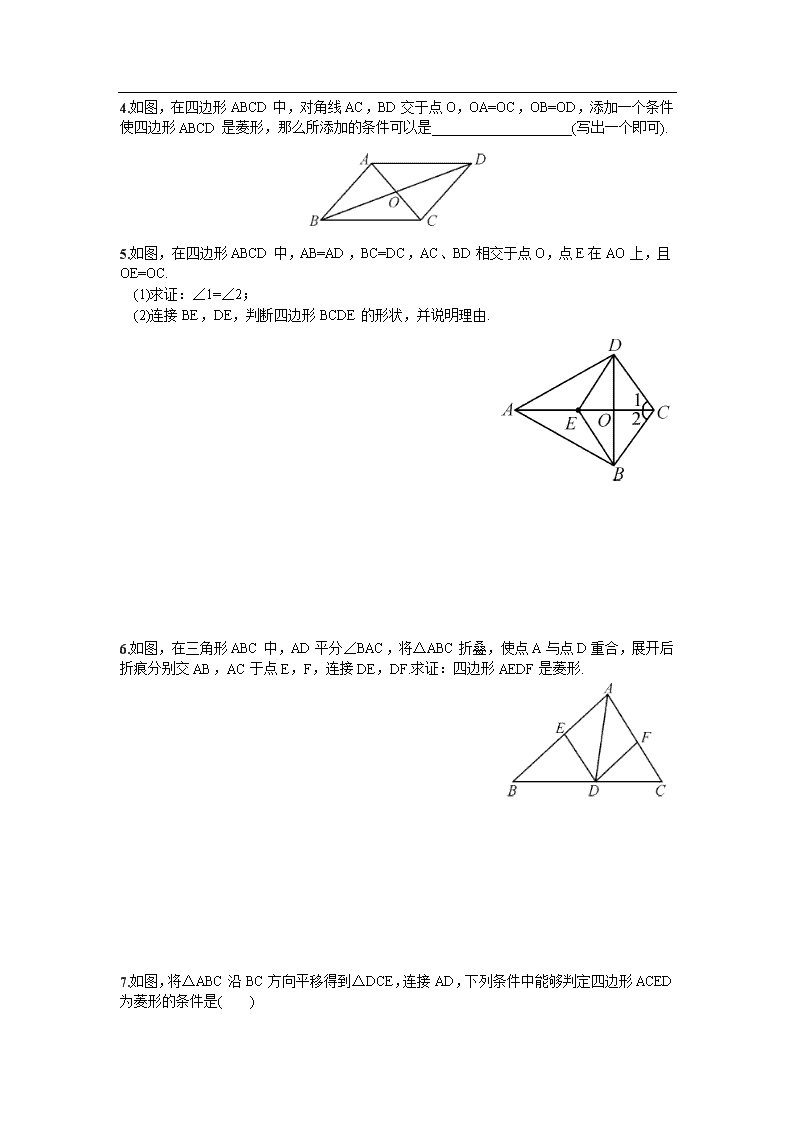4.如图，在四边形ABCD中，对角线AC，BD交于点O，OA=OC，OB=OD，添加一个条件使四边形ABCD是菱形，那么所添加的条件可以是____________________(写出一个即可).‎ ‎5.如图，在四边形ABCD中，AB=AD，BC=DC，AC、BD相交于点O，点E在AO上，且OE=OC.‎ ‎ (1)求证：∠1=∠2；‎ ‎ (2)连接BE，DE，判断四边形BCDE的形状，并说明理由.‎ ‎6.如图，在三角形ABC中，AD平分∠BAC，将△ABC折叠，使点A与点D重合，展开后折痕分别交AB，AC于点E，F，连接DE，DF.求证：四边形AEDF是菱形.‎ ‎7.如图，将△ABC沿BC方向平移得到△DCE，连接AD，下列条件中能够判定四边形ACED为菱形的条件是( )‎ ‎ 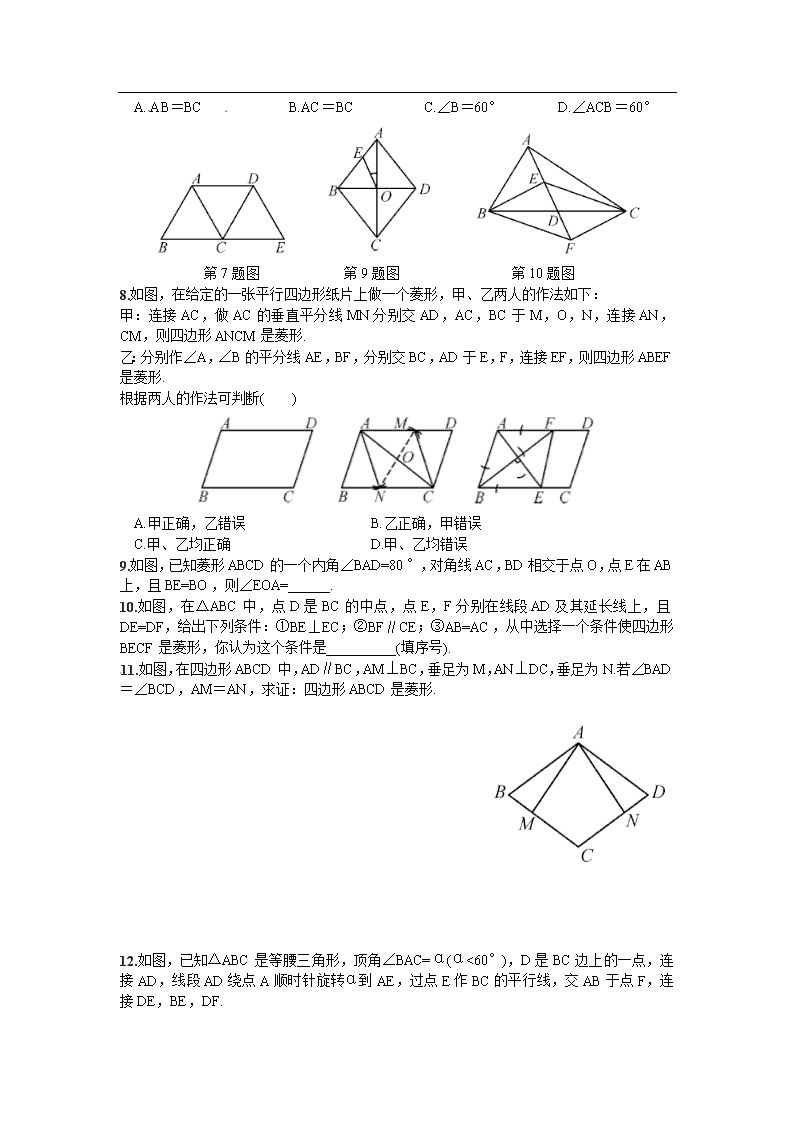A.AB＝BC B.AC＝BC C.∠B＝60° D.∠ACB＝60°[来源:Z#xx#k.Com]‎ ‎ ‎ 第7题图 第9题图 第10题图 ‎8.如图，在给定的一张平行四边形纸片上做一个菱形，甲、乙两人的作法如下：‎ 甲：连接AC，做AC的垂直平分线MN分别交AD，AC，BC于M，O，N，连接AN，CM，则四边形ANCM是菱形.‎ 乙：分别作∠A，∠B的平分线AE，BF，分别交BC，AD于E，F，连接EF，则四边形ABEF是菱形.‎ 根据两人的作法可判断( )‎ ‎ A.甲正确，乙错误 B.乙正确，甲错误[来源:学。科。网Z。X。X。K]‎ ‎ C.甲、乙均正确 D.甲、乙均错误 ‎9.如图，已知菱形ABCD的一个内角∠BAD=80°，对角线AC，BD相交于点O，点E在AB上，且BE=BO，则∠EOA=______.‎ ‎10.如图，在△ABC中，点D是BC的中点，点E，F分别在线段AD及其延长线上，且DE=DF，给出下列条件：①BE⊥EC；②BF∥CE；③AB=AC，从中选择一个条件使四边形BECF是菱形，你认为这个条件是__________(填序号).‎ ‎11.如图，在四边形ABCD中，AD∥BC，AM⊥BC，垂足为M，AN⊥DC，垂足为N.若∠BAD＝∠BCD，AM＝AN，求证：四边形ABCD是菱形.‎ ‎12.如图，已知△ABC是等腰三角形，顶角∠BAC=α(α<60°)，D是BC边上的一点，连接AD，线段AD绕点A顺时针旋转α到AE，过点E作BC的平行线，交AB于点F，连接DE，BE，DF.‎ ‎ (1)求证BE=CD；‎ ‎ (2)若AD⊥BC，试判断四边形BDFE的形状，并给出证明.‎ ‎13.如图，在四边形ABCD中，AB=AD，CB=CD，点E是CD上一点，BE交AC于点F，连接DF.‎ ‎ (1)证明：∠BAC=∠DAC，∠AFD=∠CFE；‎ ‎ (2)若AB∥CD，试证明四边形ABCD是菱形；‎ ‎ (3)在(2)的条件下，试确定E点的位置，使∠EFD=∠BCD，并说明理由.‎ 参考答案 要点感知1 都相等[来源:Zxxk.Com]‎ 预习练习1-1 B 要点感知2 互相垂直 预习练习2-1 B ‎1.B 2.菱形 24 m2‎ ‎3.证明：∵E，F分别是AB，BD的中点，[来源:Zxxk.Com]‎ ‎∴EF=AD.‎ 同理可得：GH=AD，GF=BC，HE=BC，‎ 又AD=BC，∴EF=GF=GH=HE.‎ ‎∴四边形EFGH是菱形.‎ ‎4.答案不唯一，如AB=AD或AB=BC或AC⊥BD等 ‎5.(1)证明：∵在△ADC和△ABC中，AD＝AB，AC=AC，DC=BC，‎ ‎∴△ADC≌△ABC(SSS).‎ ‎∴∠1=∠2；‎ ‎ (2)四边形BCDE是菱形；‎ ‎ 证明：∵DC=BC，∠1=∠2，‎ ‎∴AC垂直平分BD.‎ 又∵OE=OC，‎ ‎∴四边形DEBC是平行四边形.‎ ‎∵AC⊥BD，‎ ‎∴四边形DEBC是菱形.‎ ‎6.证明：连接EF，交AD于点O，‎ ‎∵AD平分∠BAC，∴∠EAO=∠FAO.‎ ‎∵EF⊥AD，∴∠AOE=∠AOF=90°.‎ 在△AEO和△AFO中，∠EAO=∠FAO，AO=AO，∠AOE=∠AOF，‎ ‎∴△AEO≌△AFO(ASA).‎ ‎∴EO=FO.‎ ‎∵A点与D点重合，‎ ‎∴AO=DO.‎ ‎∴EF，AD相互平分，‎ ‎∴四边形AEDF是平行四边形.‎ 又EF⊥AD，‎ ‎∴平行四边形AEDF为菱形.‎ ‎7.B 8.C 9.25° 10.③‎ ‎11.证明：∵AD∥BC，‎ ‎∴∠BAD＋∠B＝180°.‎ ‎∵∠BAD＝∠BCD，‎ ‎∴∠BCD＋∠B＝180°.‎ ‎∴AB∥DC.‎ ‎∴四边形ABCD是平行四边形.‎ ‎∴∠B＝∠D.‎ ‎∵AM＝AN，AM⊥BC，AN⊥DC，[来源:学*科*网]‎ ‎∴Rt△ABM≌Rt△ADN.‎ ‎∴AB＝AD.‎ ‎∴平行四边形ABCD是菱形.‎ ‎12.(1)证明：由题知AE＝AD,AB＝AC,∠BAC＝∠EAD＝α.‎ ‎∴∠BAC-∠BAD=∠EAD-∠BAD,即∠EAB=∠DAC.‎ ‎∴△EAB≌△DAC.‎ ‎∴BE＝CD.‎ ‎ (2)四边形BDFE是菱形.‎ ‎∵AB＝AC，AD⊥BC,∴BD＝CD.‎ ‎∵BE＝CD,∴BE＝BD.‎ ‎∵△EAB≌△DAC，‎ ‎∴∠EBF＝∠C.‎ ‎∵∠ABC＝∠C,‎ ‎∴∠EBF＝∠ABC.‎ ‎∵BF＝BF,‎ ‎∴△EBF≌△DBF.‎ ‎∴EF＝DF.‎ ‎∵EF∥BC,∴∠EFB＝∠FBD.‎ ‎∴∠EFB＝∠EBF.‎ ‎∴EF＝EB.‎ ‎∴BD＝BE＝EF＝FD.‎ ‎∴四边形BDFE是菱形.‎ ‎13.(1)证明：∵AB=AD，CB=CD，AC=AC，‎ ‎∴△ABC≌△ADC(SSS).‎ ‎∴∠BAC=∠DAC.‎ ‎∵AB=AD，∠BAF=∠DAF，AF=AF，‎ ‎∴△ABF≌△ADF(SAS).‎ ‎∴∠AFB=∠AFD.‎ 又∵∠CFE=∠AFB，‎ ‎∴∠AFD=∠CFE.‎ ‎∴∠BAC=∠DAC，∠AFD=∠CFE.‎ ‎ (2)∵AB∥CD，∴∠BAC=∠ACD.‎ 又∵∠BAC=∠DAC，∴∠DAC=∠ACD.‎ ‎∴AD=CD.‎ ‎∵AB=AD，CB=CD，‎ ‎∴AB=CB=CD=AD.‎ ‎∴四边形ABCD是菱形.‎ ‎ (3)当BE⊥CD时，∠EFD=∠BCD.‎ 理由：∵四边形ABCD为菱形，‎ ‎∴BC=CD，∠BCF=∠DCF.‎ 又∵CF为公共边，‎ ‎∴△BCF≌△DCF(SAS).‎ ‎∴∠CBF=∠CDF.‎ ‎∵BE⊥CD，‎ ‎∴∠BEC=∠DEF=90°.‎ ‎∴∠ECB+∠CBF=∠EFD+∠EDF=90°.‎ ‎∴∠EFD=∠BCD.‎