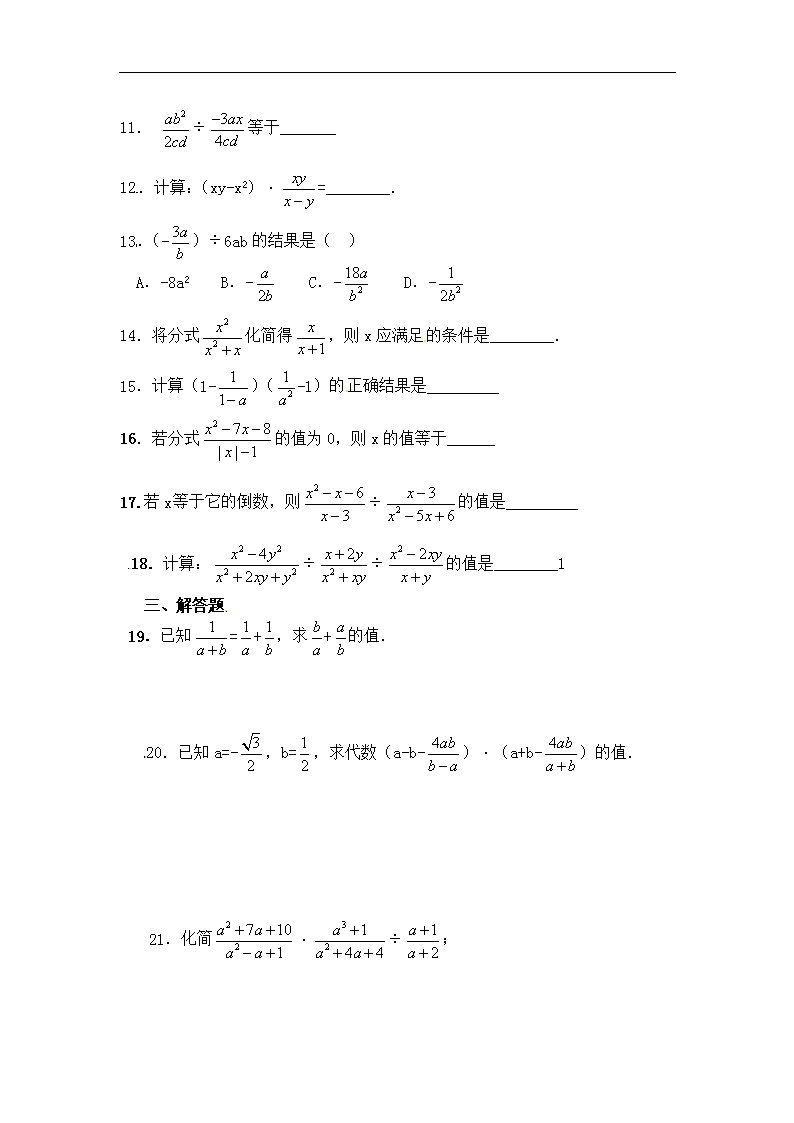人教版数学八年级上册《分式的运算》同步练习及（含答案）1 5页

第 15 章——15.2《分式的运算》同步练习及（含答案） 15.2.1 分式的乘除 一、选择题 1. x 克盐溶解在 a 克水中,取这种盐水 m 克,其中含盐( )克 A. a mx B. x am C. ax am  D. ax mx  2. 桶中装有液状纯农药 a 升,刚好一满桶,第一次倒出 8 升后用水加满,第二次 又 倒出混合药 4 升,则这 4 升混合药液中的含药量为( )升 A. a 32 B. a a )8(4  C. 8 4 a D. 2 )8(4 a a  3 .大拖拉机 m 天耕地 a 公顷,小拖拉机 n 天耕地 b 公顷,大拖机的工作效率是小 拖机的工作效率( )倍. A. b a B. m n C. bm an D. mn ab 4．下列各式与 x y x y   相等的是（ ） A． 5 5 x y x y     B．. 2 2 x y x y   C． 2 2 2 ( )x y x y   （x≠y） D． 2 2 2 2 x y x y   5．如果把分式 2x y x  中的 x 和 y 的值都扩大了 3 倍，那么分式的值（ ） A．扩大 3 倍 B．扩大 2 倍 C．扩大 6 倍 D．不变 6.下列公式中是最简分式的是（ ） A． 2 12 27 b a B． 22( )a b b a   C． 2 2x y x y   D． 2 2x y x y   7．已知 x2-5x-1 997=0，则代数式 3 2( 2) ( 1) 1 2 x x x      的值 是（ ） A．1999 B．2000 C．2001 D．2002 8．使代数式 3 3 x x   ÷ 2 4 x x   有意义的 x 的值是（ ） A．x≠3 且 x≠-2 B．x≠3 且 x≠4 C．x≠3 且 x≠-3 D．x≠-2 且 x≠3 且 x≠4 二、填空题[来源:Z.xx.k.Com] 9．-3xy÷ 22 3 y x 的值为_________ 10. 2 2 3 4 xy z ·（- 28z y ）的值为_______ 11． 2 2 ab cd ÷ 3 4 ax cd  等于_______ 12．计算：（xy-x2）· xy x y =________． 13．（- 3a b ）÷6ab 的结果是（ ） A．-8a2 B．- 2 a b C．- 2 18a b D．- 2 1 2b 14．将分式 2 2 x x x 化简得 1 x x  ，则 x 应满足的条件是________．[来源:Z_xx_k.Com] 15．计算（1- 1 1 a ）（ 2 1 a -1）的正确结果是_________ 16．若分式 2 7 8 | | 1 x x x    的值为 0，则 x 的值等于______ 17.若 x等于它的倒数，则 2 6 3 x x x    ÷ 2 3 5 6 x x x    的值是_________ 18．计算： 2 2 2 2 4 2 x y x xy y    ÷ 2 2x y x xy   ÷ 2 2x xy x y   的值是________1 三、解答题 19．已知 1 a b = 1 a + 1 b ，求 b a + a b 的值． [来源:学.科.网 Z.X.X.K] 20．已知 a=- 3 2 ，b= 1 2 ，求代数（a-b- 4ab b a ）·（a+b- 4ab a b ）的值． 21．化简 2 2 7 10 1 a a a a     · 3 2 1 4 4 a a a    ÷ 1 2 a a   ；[来源:学科网 ZXXK] [来源:学*科*网 Z*X*X*K] 22. 2 2 5 6 16 x x x    · 2 2 5 4 4 x x x    ÷ 3 4 x x   。 [来源:学§科§网] 23．若 x2-3x+1=0，求 x2+ 2 1 x 的值． [来源:学。科。网] 24．若 x：y：z=2：4：6，求 3 3 x y z x y z     的值． 25．已知 a、b、c 均不等于 0，且 1 a + 1 b + 1 c =0，求证：a2+b2+c2=（a+b+c） 2． 26．先化简，再计算： 2 2 2 2 ( )( )x y x xy y x y     - xy x y ，其中：x=5，y=-3． 15.2.1 分式的乘除 一、选择题 1.D 2. B 3.C 4．C 5．D 6．C 7. 8.D 二、填空题 9. - 29 2 x y ； 10. -6xy ； 11. - 22 3 b x ；12. -yx2 13. - 2 1 2b 14. x≠0; 15. - 1a a  16.8 17.-3 18.1 三、解答题 19. 分析：用分析综合法解：已知→可知  需解←求解 解：由已知得 1 a b = a b ab  ∴（a+b）2=ab ∴ b a + a b = 2 2a b ab  = 2( ) 2a b ab ab   = 2ab ab ab  =-1 20. 分析：一般先化简，再代值计算，化简时，把 a-b 和 a+b 视为 1 a b 和 1 a b ， 同时将 b-a 转化为-（a-b），通分先加减后乘． 解：原式=（ 1 a b + 4ab a b ）（ 1 a b - 4ab a b ） = 2( ) 4a b ab a b    · 2( ) 4a b ab a b    = 2( )a b a b   · 2( )a b a b   =（a+b）（a-b）=a2-b2 当 a=- 3 2 ，b= 1 2 时， 原式=（- 3 2 ）2-（ 1 2 ）2= 3 4 - 1 4 = 1 2 ． 21．原式= 2 ( 2)( 5) 1 a a a a     · 2 2 ( 1)( 1) ( 2) a a a a     · 2 1 a a   =a+5 22.原式= ( 2)( 3) ( 4)( 4) x x x x     · ( 1)( 4) ( 2)( 2) x x x x     · 4 3 x x   = 1 2 x x   23．由 x2-3x+1=0 两边同除以 x 得 x-3+ 1 x =0 x+ 1 x =3，x2+ 2 1 x +2=9 ∴x2+ 2 1 x =7 24．由已知设 x=2k，则 y=4k，z=6k 代入原式= 2 12 6 2 12 6 k k k k k k     = 8 16 k k =- 1 2 [来源:学#科#网] 25．由 1 a + 1 b + 1 c =0，得 bc+ac+ab=0 ∴右边=a2+b2+c2+2ab+2bc+2ac =a2+b2+c2+2（ab+bc+ac） =a2+b2+c2 ∴右边=a2+b2+c2=左边，∴等式成立． 26．解：原式= 2 2( )( ) ( )( ) x y x xy y x y x y      - xy x y = 2 2x xy y x y    - xy x y = 2( )x y x y   =x-y 当 x=5，y=-3 时，原式=5+3=8 [来源:学,科,网]