2020八年级数学上册第2章特殊三角形2 4页

‎2.2 等腰三角形 A组 ‎1．若一个等腰三角形的两边长分别为4，8，则它的周长为(C)‎ A. 12 B. 16‎ C. 20 D. 16或20‎ ‎2．如果等腰三角形的一边长是8，周长是18，那么它的腰长是(D)‎ A. 8 B. 5‎ C. 2 D. 8或5‎ ‎3．若等腰三角形的腰长与底边长之比为2∶3，其周长为28，则该等腰三角形的底边长为__12__．‎ ‎4．已知一等腰三角形的两边长x，y满足方程组则此等腰三角形的周长为__5__．‎ ‎5．如图，在△ABC中，AB＝AC，AD是BC边上的中线，点E，F是AD的三等分点．若△ABC的面积为‎12 cm2，则图中阴影部分的面积为__6__cm2.‎ ‎,(第5题))　　,(第6题))‎ ‎6．如图，AB，AC是等腰三角形ABC的两腰，AD平分∠BAC，则△BCD是等腰三角形吗？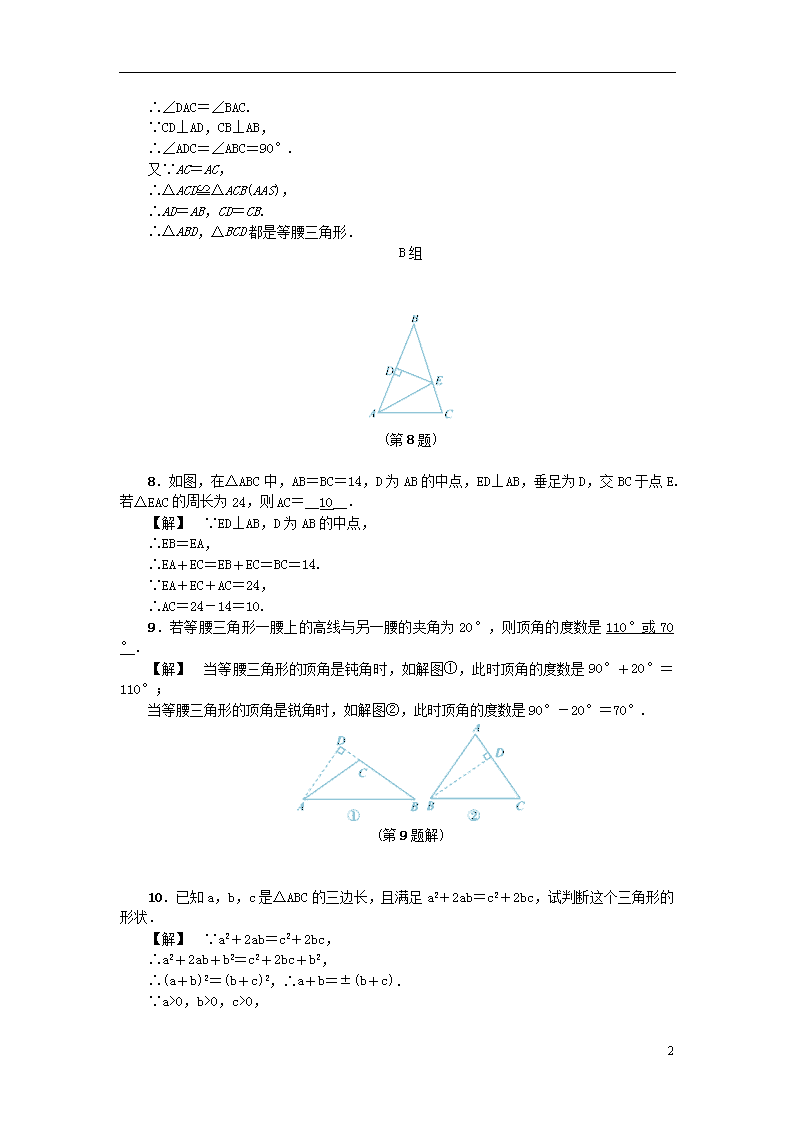试说明理由．‎ ‎【解】　△BCD是等腰三角形．理由如下：‎ ‎∵AD平分∠BAC，‎ ‎∴∠BAD＝∠CAD.‎ ‎∵AB，AC是等腰三角形ABC的两腰，‎ ‎∴AB＝AC.‎ 在△ABD和△ACD中，∵ ‎∴△ABD≌△ACD(SAS)，∴BD＝CD，‎ ‎∴△BCD是等腰三角形．‎ ‎ (第7题)‎ ‎7．如图，AC平分∠BAD，CD⊥AD，CB⊥AB，连结BD.请找出图中所有的等腰三角形，并说明理由．‎ ‎【解】　等腰三角形有△ABD和△BCD.理由如下：‎ ‎∵AC平分∠BAD，‎ 4‎ ‎∴∠DAC＝∠BAC.‎ ‎∵CD⊥AD，CB⊥AB，‎ ‎∴∠ADC＝∠ABC＝90°.‎ 又∵AC＝AC，‎ ‎∴△ACD≌△ACB(AAS)，‎ ‎∴AD＝AB，CD＝CB.‎ ‎∴△ABD，△BCD都是等腰三角形．‎ B组 ‎(第8题)‎ ‎8．如图，在△ABC中，AB＝BC＝14，D为AB的中点，ED⊥AB，垂足为D，交BC于点E.若△EAC的周长为24，则AC＝__10__．‎ ‎【解】　∵ED⊥AB，D为AB的中点，‎ ‎∴EB＝EA，‎ ‎∴EA＋EC＝EB＋EC＝BC＝14.‎ ‎∵EA＋EC＋AC＝24，‎ ‎∴AC＝24－14＝10.‎ ‎9．若等腰三角形一腰上的高线与另一腰的夹角为20°，则顶角的度数是110°或70°．‎ ‎【解】　当等腰三角形的顶角是钝角时，如解图①，此时顶角的度数是90°＋20°＝110°；‎ 当等腰三角形的顶角是锐角时，如解图②，此时顶角的度数是90°－20°＝70°.‎ ‎(第9题解)‎ ‎　　　　　　　　　　　　‎ ‎10．已知a，b，c是△ABC的三边长，且满足a2＋2ab＝c2＋2bc，试判断这个三角形的形状．‎ ‎【解】　∵a2＋2ab＝c2＋2bc，‎ ‎∴a2＋2ab＋b2＝c2＋2bc＋b2，‎ ‎∴(a＋b)2＝(b＋c)2，∴a＋b＝±(b＋c)．‎ ‎∵a>0，b>0，c>0，‎ 4‎ ‎∴a＋b＝b＋c，∴a＝c.‎ ‎∴△ABC为等腰三角形．‎ ‎11．如图，直线l1，l2交于点B，A是直线l1上的点，在直线l2上寻找一点C，使△ABC是等腰三角形，请画出所有的等腰三角形．‎ ‎(第11题)‎ ‎【解】　分类讨论：若以AB为腰，B为顶角顶点，可作出点C1，C2；‎ 若以AB为腰，A为顶角顶点，可作出点C3；‎ 若以AB为底边，可作AB的中垂线交l2于点C4.‎ 故共有4个满足题意的等腰三角形．‎ ‎12．有一个等腰三角形，三边长分别为3x－2，4x－3，6－2x，求这个等腰三角形的周长．‎ ‎【解】　当3x－2＝4x－3时，解得x＝1.‎ ‎∴3x－2＝1，4x－3＝1，6－2x＝4，显然不能组成三角形．‎ 当3x－2＝6－2x时，解得x＝.‎ ‎∴3x－2＝，6－2x＝，4x－3＝，能组成三角形，周长为＋＋＝9.‎ 当4x－3＝6－2x时，解得x＝.‎ ‎∴4x－3＝3，6－2x＝3，3x－2＝，能组成三角形，周长为3＋3＋＝.‎ 综上所述，这个等腰三角形的周长为9或.‎ 数学乐园 ‎13．(1)如图①，△ABC是等边三角形，△ABC所在平面上有一点P，使△PAB，△PBC，△PAC都是等腰三角形，问：具有这样性质的点P有几个？在图中画出来．‎ ‎(2)如图②，正方形ABCD所在的平面上有一点P，使△PAB，△PBC，△PCD，△PDA都是等腰三角形，问：具有这样性质的点P有几个？在图中画出来．‎ ‎(第13题)‎ 导学号：91354009‎ ‎【解】　(1)10个．如解图①，当点P在△ABC内部时，P是边AB，BC，CA 4‎ 的垂直平分线的交点；当点P在△ABC外部时，P是以三角形各顶点为圆心，边长为半径的圆与三条垂直平分线的交点，每条垂直平分线上得3个交点．故具有这样性质的点P共有10个．‎ ‎(第13题解①)‎ ‎(2)9个．如解图②，两条对角线的交点是1个，以正方形各顶点为圆心，边长为半径画圆，在正方形里面和外面的交点共有8个．故具有这样性质的点P共有9个．‎ ‎(第13题解②)‎ 4‎