北师大版初中数学平行四边形的判别教案 3页

‎ ‎ 课题 平行四边形的判别 时 教 学 目 标 1. 知识与技能 ‎ ⑴平行四边形的判别方法1。⑵平行四边形的判别方法2‎ 2. 过程与方法 ‎ ⑴经历平行四边形判别条件的探索过程，使学生逐步掌握说理的基本方法；并在与他人交流的过程中，能合理清晰地表达自己的思维过程。‎ ‎⑵探索并掌握平行四边形的判别条件。‎ ‎⑶在拼摆平行四边形的过程中，培养学生的动手实践能力及丰富的想象力，积累数学活动经验，增强学生的创新意识。‎ 3. 情感、态度与价值观 ‎ 让学生主动参与探索的活动，在做“数学实验”的过程中，发展学生的合情推理意识、主动探究的习惯，激发学生学习数学的热情和兴趣。‎ 重点 平行四边形的判别条件。‎ 难点 平行四边形的判别条件的应用。‎ 关键 判定方法与性质的联系。‎ 教法 引导发现法 模式： 探究式 教具 三角尺，小黑板 环节 教学内容 教师活动 学生活动 设计意图 一 创 设 情 境 1. 什么是平行四边形？它具有哪些性质？‎ 2. 装潢店要招聘店员，老板出了这样一道考题：“一顾客要一张平行四边形的玻璃，你能否利用手头的工具钉制一个平行四边形吗？并说明这张玻璃符合顾客要求的道理。”你能为招聘人员设计一方案吗？‎ 提出问题1，请一学生回答。‎ 提出问题2，从而引入新课。‎ 回忆上节课内容并回答问题。‎ 思考问题2。‎ ‎1.巩固学生的旧知，使学生知道平行四边形的定义既是性质，又是判定。‎ ‎2.从实际问题引入新课, 提出具有启发性的问题,能够调动学生的积极思维，激起学生的学习欲望。‎ 1. 平行四边形的判别：‎ ‎（1）两条对角线互相平分的四边形是平行四边形。‎ ‎（2）一组对边平行且相的四边形是平行四边形。‎ 1. 指导学生摆拼木条。‎ 2. 提出问题 ‎1.将木条AC，BD的中点重叠，并用钉子固定。‎ ‎2.将两根同样长的木条AB，CD平行放置，再用木条AD，BC加固。 ‎ 与同伴进行交流。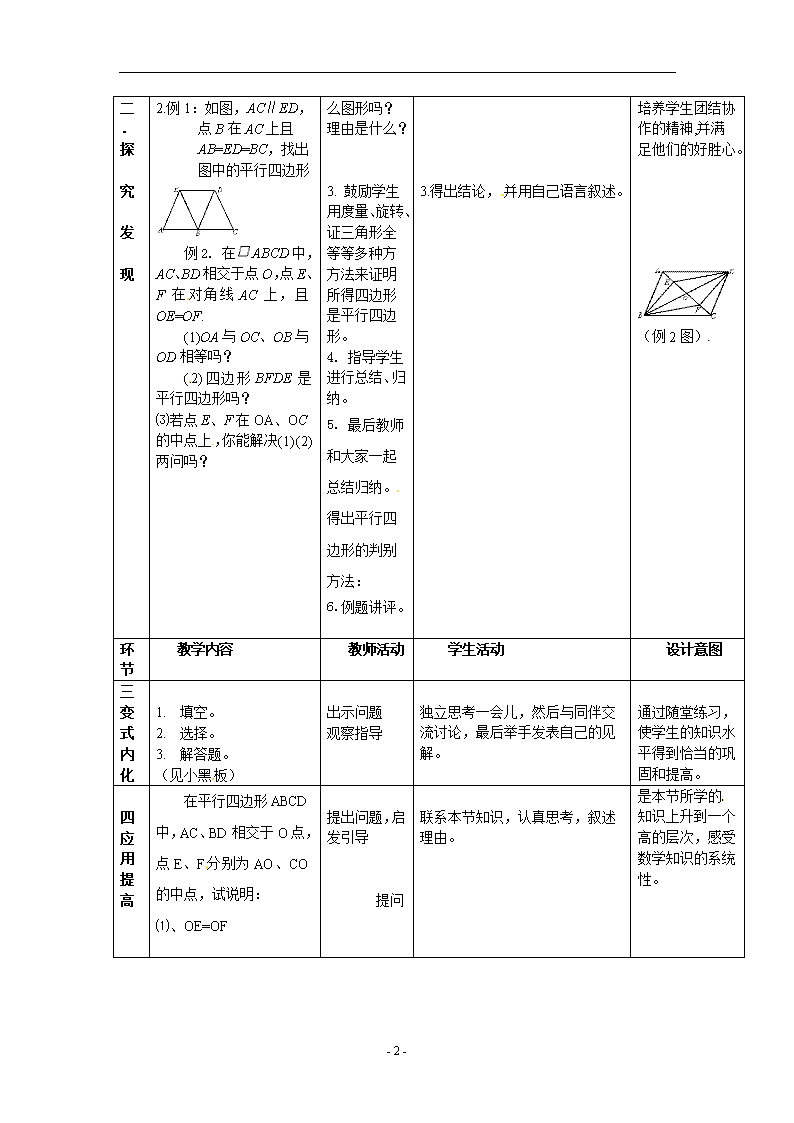 ‎ - 3 -‎ ‎ ‎ 二．‎ 探 究 发 现 ‎2.例1：如图，AC∥ED，点B在AC上且AB=ED=BC，找出图中的平行四边形 例2. 在ABCD中，AC、BD相交于点O，点E、F在对角线AC上，且OE=OF.‎ ‎(1)OA与OC、OB与OD相等吗？‎ ‎(2)四边形BFDE是平行四边形吗？‎ ‎⑶若点E、F在OA、OC的中点上，你能解决(1)(2)两问吗？‎ 你能判定你摆的是什么图形吗？理由是什么？‎ ‎3. 鼓励学生用度量、旋转、证三角形全等等多种方方法来证明所得四边形是平行四边形。‎ ‎4. 指导学生进行总结、归纳。‎ ‎5. 最后教师和大家一起总结归纳。得出平行四边形的判别方法： ‎ ‎6.例题讲评。‎ ‎3.得出结论，并用自己语言叙述。‎ 让学生在在拼摆各种图形的过程中，积累数学活动经验，增强学生的创新意识，培养学生团结协作的精神,并满足他们的好胜心。‎ ‎（例2图）‎ 环节 教学内容 教师活动 学生活动 设计意图 三 变 式 内 化 1. 填空。‎ 2. 选择。‎ 3. 解答题。‎ ‎（见小黑板）‎ 出示问题 观察指导 独立思考一会儿，然后与同伴交流讨论，最后举手发表自己的见解。‎ 通过随堂练习，使学生的知识水平得到恰当的巩固和提高。‎ 四 应 用 提 高 在平行四边形ABCD中，AC、BD相交于O点，点E、F分别为AO、CO的中点，试说明：‎ ‎⑴、OE=OF 提出问题，启发引导 提问 联系本节知识，认真思考，叙述理由。‎ 是本节所学的知识上升到一个高的层次，感受数学知识的系统性。‎ - 3 -‎ ‎ ‎ ‎⑵、四边形DEBF是平行四边形。‎ ‎⑶、如果E、F点分别在AC的延长线上时（如图2），且满足AE=CF，上述结论仍然成立吗？‎ 五 总 结 拓 展 ‎1.两条对角线互相平分的四边形是平行四边形。‎ ‎2.一组对边平行且相等的四边形是平行四边形。‎ 和学生共同总结。‎ 学生回顾探究的整个过程，体会学习的成果，感受成功的喜悦，产生后继学习的激情。‎ 关注学生参与活动的程度和在活动中表现出来的思维水平，还要关注学生能否用自己语言表达自己的想法。‎ 六 激 发 悬 念 1. 两组对边分别相等的四边形是平行四边形吗？‎ 2. 两组对角分别相等的四边形是平行四边形吗？‎ 提出问题，留下悬念。‎ 积极思考。‎ 为下节课做铺垫。‎ 作 业 ‎1.习题4.3 2题 ‎ ‎2. 撰写设计方案 板 书 设 计 ‎2.平行四边形的判别 判别方法：‎ ‎1.两组对边分别平行的四边形是平行四边形。 例2.‎ ‎2. 两条对角线互相平分的四边形是平行四边形。‎ ‎3.一组对边平行且相的四边形是平行四边形。‎ 例1.‎ 教 学 反 思 - 3 -‎