初三数学同步练习题及解析：实际问题与一元二次方程（2） 7页

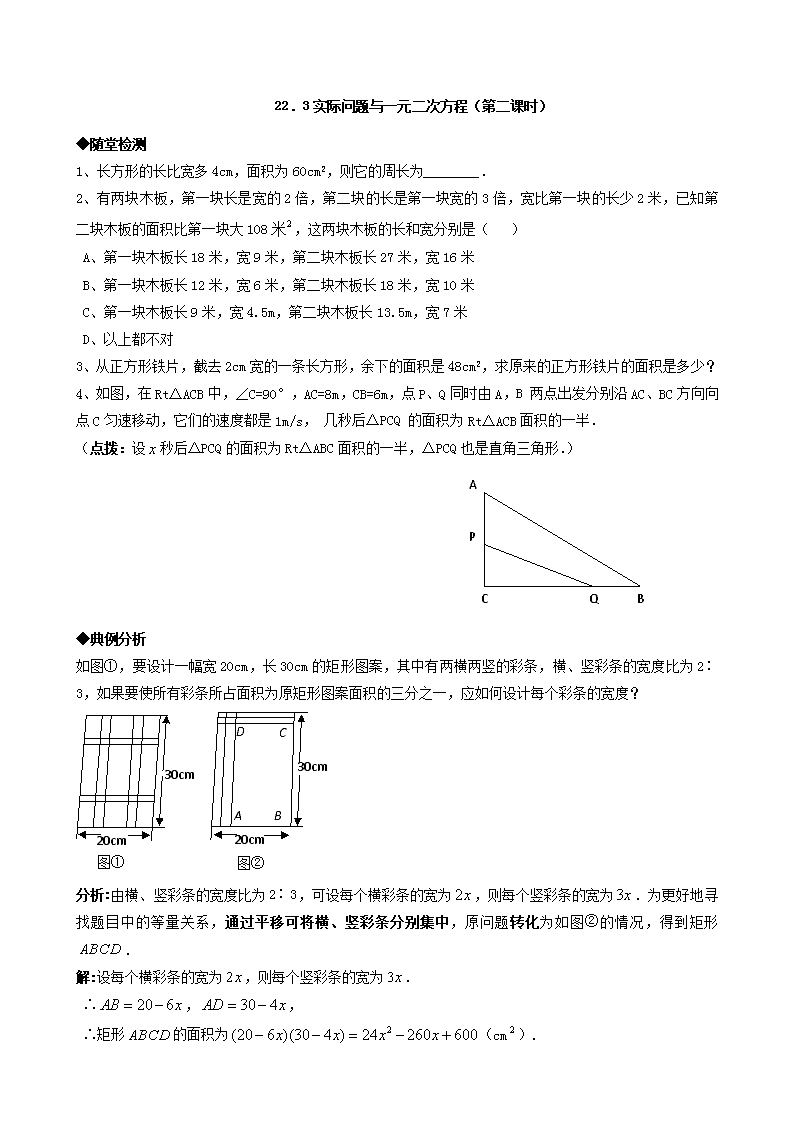
22．3 实际问题与一元二次方程（第二课时） ◆随堂检测 1、长方形的长比宽多 4cm，面积为 60cm2，则它的周长为________． 2、有两块木板，第一块长是宽的 2 倍，第二块的长是第一块宽的 3 倍，宽比第一块的长少 2 米，已知第 二块木板的面积比第一块大 108 2米 ，这两块木板的长和宽分别是（ ） A、第一块木板长 18 米，宽 9 米，第二块木板长 27 米，宽 16 米 B、第一块木板长 12 米，宽 6 米，第二块木板长 18 米，宽 10 米 C、第一块木板长 9 米，宽 4.5m，第二块木板长 13.5m，宽 7 米 D、以上都不对 3、从正方形铁片，截去 2cm 宽的一条长方形，余下的面积是 48cm2，求原来的正方形铁片的面积是多少？ 4、如图，在 Rt△ACB 中，∠C=90°，AC=8m，CB=6m，点 P、Q 同时由 A，B两点出发分别沿 AC、BC 方向向 点 C 匀速移动，它们的速度都是 1m/s，几秒后△PCQ的面积为 Rt△ACB 面积的一半． （点拨：设 x 秒后△PCQ 的面积为 Rt△ABC 面积的一半，△PCQ 也是直角三角形．） ◆典例分析 如图①，要设计一幅宽 20cm，长 30cm 的矩形图案，其中有两横两竖的彩条，横、竖彩条的宽度比为 2∶3， 如果要使所有彩条所占面积为原矩形图案面积的三分之一，应如何设计每个彩条的宽度？ 20cm 20cm 30cm D C A B 图②图① 30cm 分析:由横、竖彩条的宽度比为 2∶3，可设每个横彩条的宽为 2x ，则每个竖彩条的宽为3x ．为更好地寻 找题目中的等量关系，通过平移可将横、竖彩条分别集中，原问题转化为如图②的情况，得到矩形 ABCD ． 解:设每个横彩条的宽为 2x ，则每个竖彩条的宽为3x ． ∴ 20 6AB x  ， 30 4AD x  ， ∴矩形 ABCD 的面积为 2(20 6 )(30 4 ) 24 260 600x x x x     （cm 2 ）. BC A Q P 根据题意，得 2 124 260 600 1 20 303x x          . 整理，得 26 65 50 0x x   . 解方程，得 1 2 5 106x x ， , ∵ 2 10x  不合题意，舍去.∴ 5 6x  . 则 5 52 33 2x x ， ． 答：每个横、竖彩条的宽度分别为 5 3 cm， 5 2 cm. ◆课下作业 ●拓展提高 1、矩形的周长为 8 2 ，面积为 1，则矩形的长和宽分别为________． 2、如图，在 ABCD 中，AE BC 于 E，AE EB EC a   ，且 a 是一元二次方程 2 2 3 0x x   的根， 则 ABCD 的周长为（ ） A、 4 2 2 B、12 6 2 C、 2 2 2 D、 2 2 12 6 2 或 A D CE C B 3、某农场要建一个长方形的养鸡场，鸡场的一边靠墙（墙长 25m），另三边用木栏围成，木栏长 40m． （1）鸡场的面积能达到 180m2 吗？能达到 200m2 吗？ （2）鸡场的面积能达到 210m2 吗？ 4、某林场计划修一条长 750m，断面为等腰梯形的渠道，断面面积为 1.6m2，上口宽比渠深多 2m，渠底比 渠深多 0.4m． （1）渠道的上口宽与渠底宽各是多少？ （2）如果计划每天挖土 48m3，需要多少天才能把这条渠道挖完？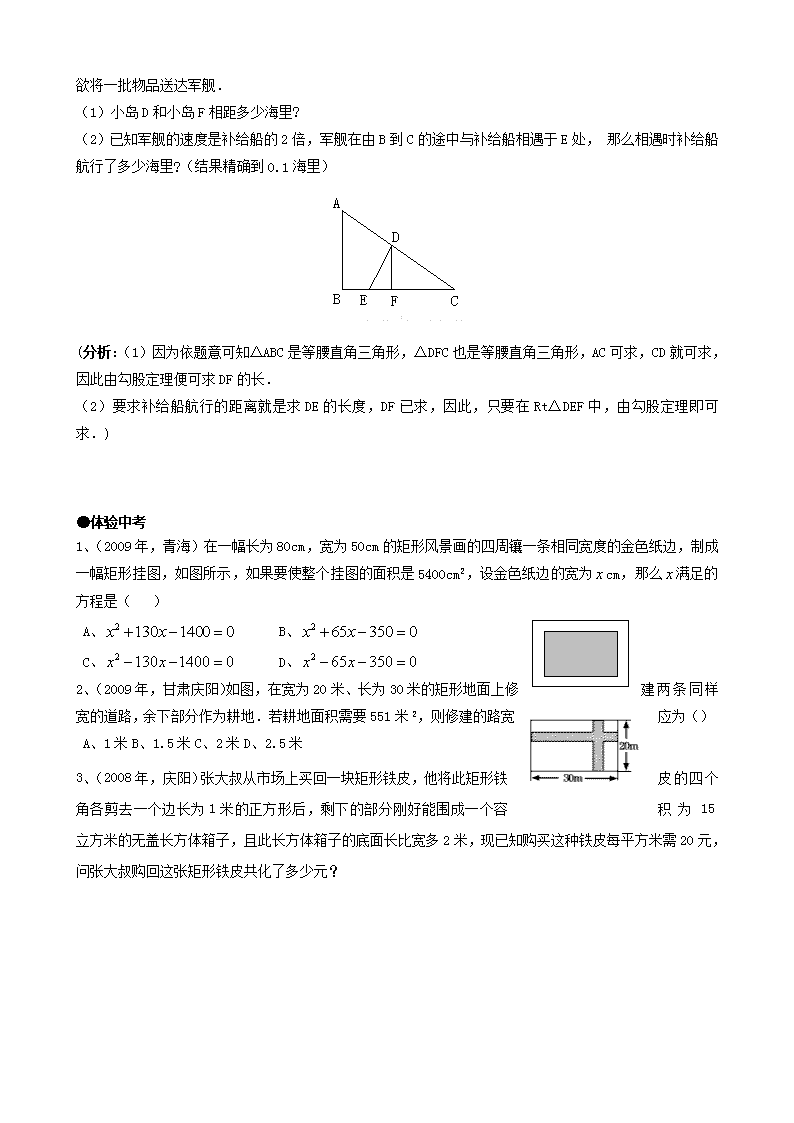 (分析：因为渠深最小，为了便于计算，不妨设渠深为 x m.) 5、如图，某海军基地位于 A 处，在其正南方向 200 海里处有一重要目标 B，在 B 的正东方向 200 海里处 有一重要目标 C，小岛 D 位于 AC 的中点，岛上有一补给码头：小岛 F 位于 BC 上且恰好处于小岛 D 的正南 方向，一艘军舰从 A 出发，经 B 到 C 匀速巡航，一般补给船同时从 D 出发，沿南偏西方向匀速直线航行， 欲将一批物品送达军舰． （1）小岛 D 和小岛 F 相距多少海里? （2）已知军舰的速度是补给船的 2 倍，军舰在由 B 到 C 的途中与补给船相遇于 E 处，那么相遇时补给船 航行了多少海里?（结果精确到 0.1 海里） B A C E D www.czsx.com.cn F (分析：（1）因为依题意可知△ABC 是等腰直角三角形，△DFC 也是等腰直角三角形，AC 可求，CD 就可求， 因此由勾股定理便可求 DF 的长． （2）要求补给船航行的距离就是求 DE 的长度，DF 已求，因此，只要在 Rt△DEF 中，由勾股定理即可求．) ●体验中考 1、（2009 年，青海）在一幅长为 80cm，宽为 50cm 的矩形风景画的四周镶一条相同宽度的金色纸边，制成 一幅矩形挂图，如图所示，如果要使整个挂图的面积是 5400cm2，设金色纸边的宽为 x cm，那么 x 满足的 方程是（ ） A、 2 130 1400 0x x   B、 2 65 350 0x x   C、 2 130 1400 0x x   D、 2 65 350 0x x   2、（2009 年，甘肃庆阳）如图，在宽为 20 米、长为 30 米的矩形地面上 修建两条同 样宽的道路，余下部分作为耕地．若耕地面积需要 551 米 2，则修建的 路宽应为 （） A、1 米 B、1.5 米 C、2 米 D、2.5 米 3、（2008 年，庆阳）张大叔从市场上买回一块矩形铁皮，他将此矩形铁 皮的四个 角各剪去一个边长为 1 米的正方形后，剩下的部分刚好能围成一个容积为 15 立方米的无盖长方体箱子， 且此长方体箱子的底面长比宽多 2 米，现已知购买这种铁皮每平方米需 20 元，问张大叔购回这张矩形铁 皮共化了多少元？ 参考答案： ◆随堂检测 1、32cm. 设长方形铁片的宽是 x cm，则长是 ( 4)x  cm． 根据题意，得： ( 4) 60x x   ， 解得， 1 26, 10x x   . ∵ 2 10x   不合题意，舍去．∴ 6x  .∴长方形铁片的长是 10cm，宽是 6cm，则它的周长为 32cm. 2、B. 设第一块木板的宽是 x 米，则长是 2x 米，第二块木板的长是3x 米，宽是 2x （2 ）米． 根据题意，得： 3 (2 2) 2 108x x x x    整理，得： 22 3 54 0x x   ， 因式分解得， ( 6)(2 9) 0x x   ， 解得， 1 2 96, 2x x   . ∵ 2 9 2x   不合题意，舍去．∴ 6x  . ∴第一块木板的宽是 6 米，则长是 12 米，第二块木板的长是 18 米，宽是 10 米．故选 B. 3、解：原来的正方形铁片的边长是 x cm，则面积是 2x cm2． 根据题意，得： ( 2) 48x x   ， 整理，得： 2 2 48 0x x   ， 因式分解得， ( 8)( 6) 0x x   ， 解得， 1 28, 6x x   . ∵ 2 6x   不合题意，舍去．∴ 8x  .∴ 2 64x  . 答：原来的正方形铁片的面积是 64cm2． 4、解：设 x 秒后△PCQ 的面积为 Rt△ACB 面积的一半． 根据题意，得： 1 2 （8- x ）（6- x ）= 1 2 × 1 2 ×8×6 整理，得： 2 14 24 0x x   ， 配方得， 2( 7) 25x   ， 解得， 1 212, 2x x  . ∵ 1 12x  不合题意，舍去．∴ 2x  . 答：2 秒后△PCQ 的面积为 Rt△ACB 面积的一半． ◆课下作业 ●拓展提高 1、 2 2 7 , 2 2 7 . 设矩形的长 x ，则宽为 4 2 x ． 根据题意，得 (4 2 ) 1x x  . 整理，得 2 4 2 1 0x x   . 用公式法解方程，得 1 22 2 2 2 7x x  + 7， , 当长为 1 2 2x  + 7 时,则宽为 2 2 7 . 当长为 2 2 2 7x   时,则宽为 1 2 2x  + 7 ,不合题意，舍去. ∴矩形的长和宽分别为 2 2 7 和 2 2 7 . 2、A. ∵ a 是一元二次方程 2 2 3 0x x   的根，∴ 1a  ，∴AE=EB=EC=1，∴AB= 2 ，BC=2.∴ ABCD 的周长为 4 2 2 ，故选 A。 3、解：（1）都能达到． 设宽为 x m，则长为（40-2 x ）m， 依题意，得： x （40-2 x ）=180 整理，得： x 2-20 x +90=0， x 1=10+ 10 ， x 2=10- 10 ； 同理 x （40-2 x ）=200， x 1= x 2=10． （2）不能达到 210m2．∵依题意， x （40-2 x ）=210，整理得， x 2-20 x +105=0， b2-4ac=400-410=-10<0，无解，即不能达到． 4、解：（1）设渠深为 x m，则上口宽为( x +2)m，渠底为( x +0.4)m. 根据梯形的面积公式可得: 1 2 （ x +2+ x +0.4） x =1.6, 整理，得：5 x 2+6 x -8=0, 解得： x 1= 4 5 =0.8， x 2=-2（舍） ∴上口宽为 2.8m，渠底为 1.2m． （2）如果计划每天挖土 48m3，需要1.6 750 48  =25(天)才能把这条渠道挖完. 答：渠道的上口宽与渠底深各是 2.8m 和 1.2m；需要 25 天才能挖完渠道． 5、解：（1）连结 DF，则 DF⊥BC. ∵AB⊥BC，AB=BC=200 海里． ∴AC= 2 AB=200 2 海里，∠C=45°. ∴CD= 1 2 AC=100 2 海里. DF=CF， 2 DF=CD. ∴DF=CF= 2 2 CD= 2 2 ×100 2 =100（海里）. ∴小岛 D 和小岛 F 相距 100 海里． （2）设相遇时补给船航行了 x 海里，那么 DE= x 海里，AB+BE=2 x 海里. EF=AB+BC-（AB+BE）-CF=（300-2 x ）海里. 在 Rt△DEF 中，根据勾股定理可得方程 x 2=1002+（300-2 x ）2 整理，得 3 x 2-1200 x +100000=0. 解这个方程，得： x 1=200-100 6 3 , x 2=200+100 6 3 . ∵ x 2=200+100 6 3 不合题意，舍去. ∴ x =200-100 6 3 ≈118.4. ∴相遇时补给船大约航行了 118.4 海里． ●体验中考 1、B. 依题意, x 满足的方程是 (50 2 )(80 2 ) 5400x x   , 整理得 2 65 350 0x x   .故选 B. 2、A. 设修建的路宽应为 x 米． 根据题意，得： (30 )(20 ) 551x x   ， 整理，得： 2 50 49 0x x   ， 因式分解得， ( 1)( 49) 0x x   ， 解得， 1 21, 49x x  . ∵ 2 49x  不合题意，舍去．∴ 1x  . ∴则修建的路宽应为 1 米.故选 A. 3、解：设此长方体箱子的底面宽是 x 米，则长是 ( 2)x  米． 根据题意，得： ( 2) 15x x   ， 整理，得： 2 2 15 0x x   ， 因式分解得， ( 3)( 5) 0x x   ， 解得， 1 23, 5x x   . ∵ 2 5x   不合题意，舍去．∴ 3x  . ∴ 此 矩 形 铁 皮 的 面 积 是 ( 2)( 2 2) 5 7 35x x      （ 平 方 米 ）， ∴ 购 回 这 张 矩 形 铁 皮 共 化 了 35 20 700  （元）. 答：张大叔购回这张矩形铁皮共化了 700 元.