- 87.46 KB
- 2021-10-26 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
- 1 -
1.3 探索三角形全等的条件(1)
教学目标
【知识与能力】
1.掌握“边角边(SAS)”的内容,会应用“边角边(SAS)”来判定两个三角形全等。
2.进一步掌握证明的书写规范。
【过程与方法】
初步掌握利用全等三角形来进一步说明线段或角相等。
【情感态度价值观】
引导学生经历观察、只做、画图、猜想等活动,并鼓励学生充分的交流讨论、质疑说明、归
纳结论,协调发展学生的合情推理与演绎推理能力.
教学重难点
【教学重点】
掌握三角形全等的“边角边”条件.
【教学难点】
正确运用“边角边”条件判定三角形全等,解决实际问题.
课前准备
无
教学过程
一、知识回顾
1.什么叫做全等三角形?全等三角形有什么性质?
2.如何找出全等三角形中的对应元素?
3.表示两个三角形全等时就注意什么问题?——对应
二、假设情境
若两个三角形全等,则它们的对应边、对应角相等;反之,两个三角形有多少对应边或角分
别相等时,这两个三角形全等?
三、新知探索
1.一个三角形有 6 个元素,三边三角,用其中一个或两个画三角形,动手试试,看看你画的
与别人画的是否一样?
(1)一条边为 3; (2)一个角为 60°; (3)一边为 3,一个角为 60°;
(4)两边分别为 3 和 4; (5)两角分别为 30°和 40°;
(6)借用量角器和刻度尺画一个三角形,使得其一个角为 40°,两邻边长为 3 和 4。
结论:三角形全等的条件:两边及夹角分别(对应)相等的两个三角形全等,简写成“边
角边”或“SAS”.
符号语言:如图,在△ABC 和△DEF 中,
AB=DE
∠A=∠D
AC=DF
∴△ABC≌△DEF(SAS).
FE
D
CB
A
- 2 -
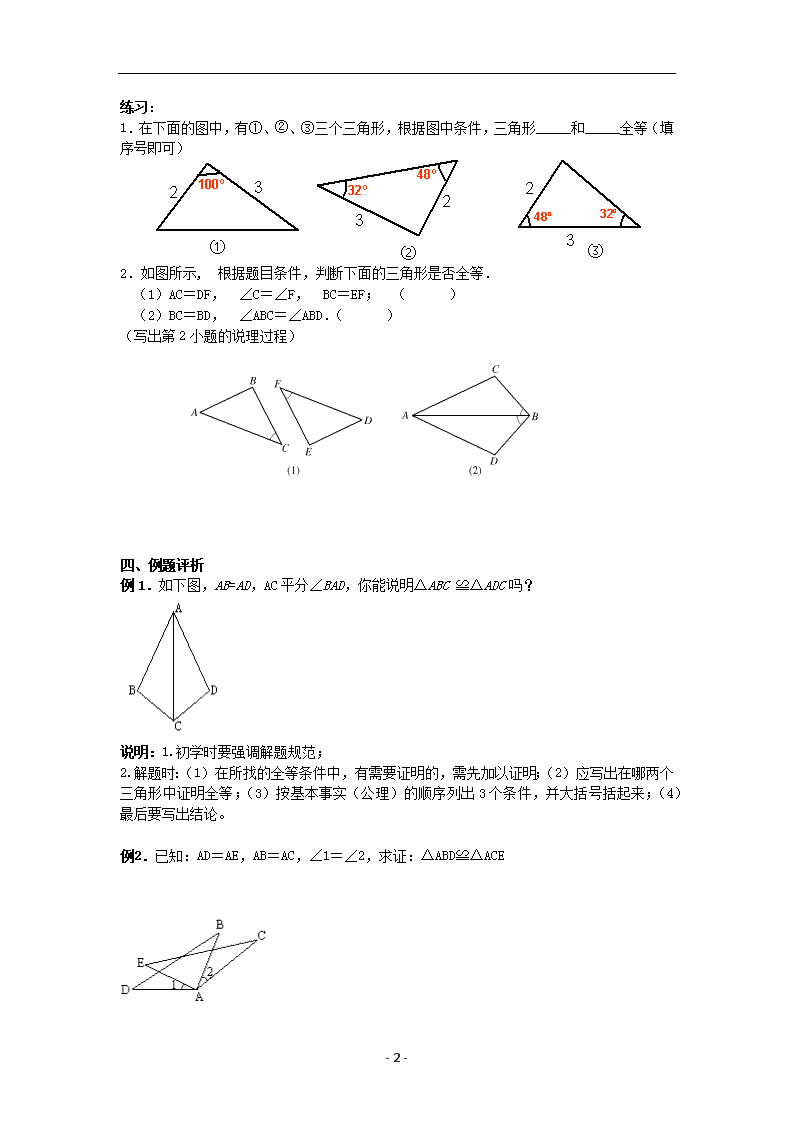
练习:
1.在下面的图中,有①、②、③三个三角形,根据图中条件,三角形_____和_____全等(填
序号即可)
2.如图所示, 根据题目条件,判断下面的三角形是否全等.
(1)AC=DF, ∠C=∠F, BC=EF; ( )
(2)BC=BD, ∠ABC=∠ABD.( )
(写出第 2 小题的说理过程)
四、例题评析
例 1.如下图,AB=AD,AC 平分∠BAD,你能说明△ABC ≌△ADC 吗?
说明:1.初学时要强调解题规范;
2.解题时:(1)在所找的全等条件中,有需要证明的,需先加以证明;(2)应写出在哪两个
三角形中证明全等;(3)按基本事实(公理)的顺序列出 3 个条件,并大括号括起来;(4)
最后要写出结论。
例2.已知:AD=AE,AB=AC,∠1=∠2,求证:△ABD≌△ACE
②
2
3
48º
32º
②
2
3
48º
32º
①
2 3100º
①
2 3100º
③
2
3
48º 32º
③
2
3
48º 32º
- 3 -
练习:已知:如图,M 是 AB 的中点,MC=MD,∠1=∠2 试说明:AC=BD
拓展:在在△ABC 中,AB=8,AC=6,则 BC 上的中线 AD 的取值范围是 。
五、课堂小结与反思
本节课我们通过操作实践,发现了判定两个三角形全等的第一个方法——边角边。在解决实
际问题时,特别在说明两个三角形全等的理由时,应根据已知条件及图形中的有关条件,依
照“SAS”加以说明。
D
C
B
M
A
2
1
相关文档
- 八年级下册数学同步练习6-2 第1课2021-10-262页
- 八年级上历史课件:第12课 新文化运2021-10-2627页
- 八年级下册数学教案第十六章复习 2021-10-264页
- 2020八年级道德与法治上册第四单元2021-10-264页
- 八年级语文下册第四单元15我一生中2021-10-2626页
- 2019学年八年级数学上学期复习大纲2021-10-266页
- 八年级下册数学教案18-2 第2课时 2021-10-261页
- 八年级下物理课件八年级下册物理课2021-10-2628页
- 2020八年级地理上册 第三章 第二节2021-10-261页
- 华东师大版八年级上册第14章 勾股2021-10-265页