上海教育版数学八下第二十二章《四边形》综合复习 7页

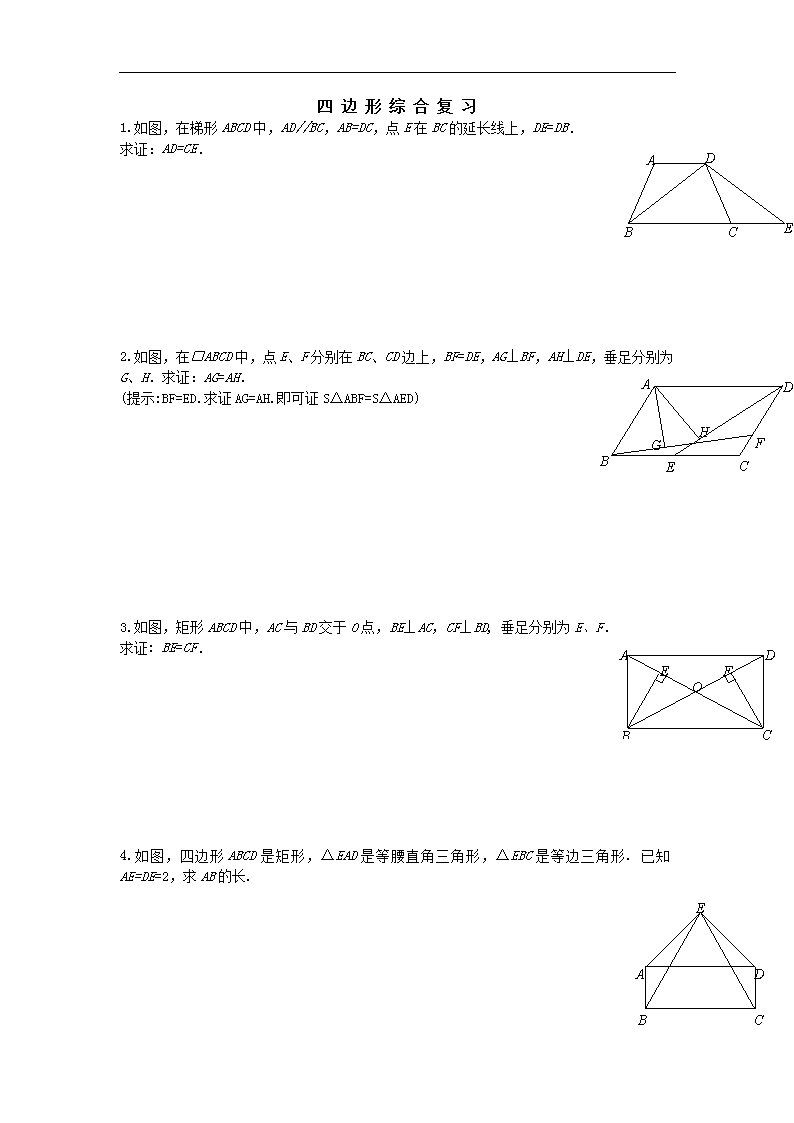
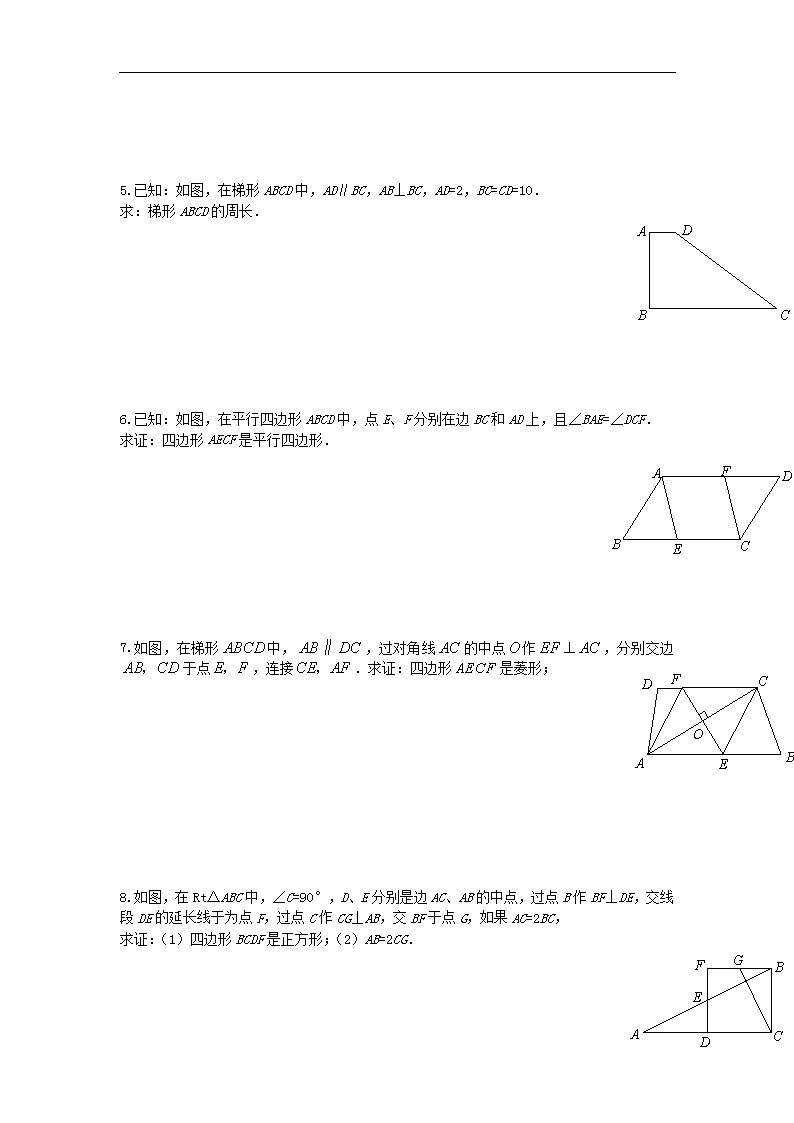
四 边 形 综 合 复 习 1.如图，在梯形 ABCD 中，AD//BC，AB=DC，点 E 在 BC 的延长线上，DE=DB． 求证：AD=CE． 2.如图，在□ABCD 中，点 E、F 分别在 BC、CD 边上，BF=DE，AG⊥BF，AH⊥DE，垂足分别为 G、H．求证：AG=AH． (提示:BF=ED.求证 AG=AH.即可证 S△ABF=S△AED) 3.如图，矩形 ABCD 中，AC 与 BD 交于 O 点，BE⊥AC，CF⊥BD, 垂足分别为 E、F． 求证: BE=CF． 4.如图，四边形 ABCD 是矩形，△EAD 是等腰直角三角形，△EBC 是等边三角形. 已知 AE=DE=2， 求 AB 的长. A B C D E A B C D E FG H B C O E A F D E A D CB 5.已知：如图，在梯形 ABCD 中，AD∥BC，AB⊥BC，AD=2，BC=CD=10． 求：梯形 ABCD 的周长． 6.已知：如图，在平行四边形 ABCD 中，点 E、F 分别在边 BC 和 AD 上，且∠BAE=∠DCF． 求证：四边形 AECF 是平行四边形． 7.如图，在梯形 ABCD 中， AB DC∥ ，过对角线 AC 的中点O 作 EF AC ，分别交边 AB CD， 于点 E F， ，连接CE AF， ．求证：四边形 AECF 是菱形； 8.如图，在 Rt△ABC 中，∠C=90°，D、E 分别是边 AC、AB 的中点，过点 B 作 BF⊥DE，交线 段 DE 的延长线于为点 F，过点 C 作 CG⊥AB，交 BF 于点 G，如果 AC=2BC， 求证：（1）四边形 BCDF 是正方形；（2）AB=2CG． A B C D A B C DF E A B CFD O E A C BF D E G 9.如图，在□ABCD 中，O 是对角线 AC 的中点，过点 O 作 AC 的垂线与边 AD、BC 分别交于 E、 F，求证：四边形 AFCE 是菱形. （推理过程可以不写理由） 10.如图，在正方形 ABCD 中，H 在 BC 上，EF⊥AH 交 AB 于点 E，交 DC 于点 F.若 AB=3，BH=1， 求 EF 的长. 11.如图，在平行四边形 ABCD 中，点 E、F 在对角线 AC 上，且 AE=CF，请你以 F 为一个端点和图中已标明字母的某一点连成一条新线段，猜想并证明它和图中已 有的某一条线段相等（只须证明一组线段相等即可） （1）连结 . （2）猜想： = . （3）证明（要求每步写出理由）： 12.已知：如图，在平行四边形 ABCD 中，点 E、F、G、H 分别在边 AB、BC、CD、DA 上，如果 AE = CG，AH = CF，且 EG 平分 HEF 。 (1) 求证：四边形 EFGH 是平行四边形； (2) 求证：四边形 EFGH 是菱形。 F B D C A E O D C B H E G F A A B C D E F G H 13.如图，四边形 ABCD 是菱形，分别延长 AB、BC、CD、DA 到 E、F、G、H 点，使 AE=BF=CG=DH．求证：四边形 EFGH 是平行四边形． 14.如图，在四边形 ABCD 中，E、F、G、H 分别是 AD、BD、BC、AC 上的中点，AB=5，CD=7．求 四边形 EFGH 的周长． 15.如图，BD 是△ABC 的角平分线，EF 是 BD 的中垂线，分别交 AB 于点 E，AC 于点 F． 求证：四边形 BFDE 是菱形． 16.如图，四边形 ABCD 是正方形，延长边 AD 到 E，使得 CE∥BD． （1）试比较正方形 ABCD 与△ABE 面积的大小，并说明理由． （2）如果条件“四边形 ABCD 是正方形”改为“四边形 ABCD 是梯形，AB∥CD”，其余条件都 G F EH A D C B A B CG DE F H A B CF E D 不变，那么梯形 ABCD 与△ABE 面积的大小有什么关系？（只需写出结论，不必证明） 17.如图，在四边形 ABCD 中，对角线 BD⊥AB，AD=20，AB=16，BC=15，CD=9，求证：四边形 ABCD 是梯形． 18.在等腰梯形 ABCD 中，AD∥BC，AB=CD=AD，AC⊥AB．求∠B 的度数． 19.如图，已知：在梯形 ABCD 中，AD∥BC，AD+BC=CD ，M 是 AB 的中点。 求证：DM、CM 分别平分∠ADC 和∠BCD 20.如图，在等腰梯形 ABCD 中， AB ∥ DC ， cmBCAD 5 ，AB=12 cm，CD=6cm，点 P 从 A 开始沿 AB 边向 B 以每秒 3cm 的速度移动，点Q 从C 开始沿 CD 边向 D 以每秒 1cm 的速 度移动，如果点 P、Q 分别从 A、C 同时出发，当其中一点到达终点时运动停止。设运动时间 为 t 秒。 （1）求证：当 t= 2 3 时，四边形 APQD 是平行四边形； A B C D O A B CD A B C D A B C D M （2）PQ 是否可能平分对角线 BD？若能，求出当 t 为何值时 PQ 平分 BD；若不能，请说明理 由； （3）若△DPQ 是以 PQ 为腰的等腰三角形，求 t 的值。 最后一题 （1）证明：∵当 t= 2 3 时，AP=3t= 2 9 ，DQ=6-t= 2 9 ，∴AP=DQ…………………（1 分） 又∵ A B ∥ DC ，∴AP//DQ，∴ APQD 是平行四边形………………（1 分） （2）能，当 t=3 时 PQ 平分 BD………………（2 分） 假设 PQ 平分对角线 BD，设交点为 M，即 DM=MB， ∵AB//CD，∴∠1=∠2， 又∵∠3=∠4，∴△DQM≌△BPM， ∴DQ=PB，即 6-t=12-3t，……………………（1 分） ∴t=3……………………………………………（1 分） 又可证明当 t=3 时 DM=MB，∴当 t=3 时 PQ 平分 BD。 （3）过 D 作 DH⊥AB 于 H， ∵梯形中 cmBCAD 5 ,AB=12 cm,CD=6cm ∴AH=3，DH= 4…………………………………（1 分） 情况 1：DP=PQ 过 P 作 PM⊥CD 于 M，则 DM=DQ= 2 6 t ∵PM⊥CD，DH⊥AB，∴PM//DH，又 A B ∥ DC ，∴DHPM 为矩形， ∴HP=DM，即 3t-3= 2 6 t ∴t= 7 12 ……………………………………………………（1 分） ∵0≤t≤4， 7 12 ≤4，∴t= 7 12 符合题意 情况 2：DQ=PQ（如图） 在 Rt△QNP 中，QP=6-t，PN=12-3t-3-t=9-4t，QN=4 ∴ 222 )49(4)6( tt  …………………（1 分） A B CD Q P 2 A B CD · ·Q P M 1 3 4 A B CD · ·Q P M H A B CD · ·Q P 整理得： 0616015 2  tt ∵ 61154602  = 0)6160(60  ∴方程无解………………………………………………………………………（1 分） 综上，若△DPQ 是以 PQ 为边的等腰三角形，则 t= 7 12 N