人教版八年级数学上册期中测试题及答案 10页

人教版八年级数学上册期中测试题及答案 ‎(考试时间：120分钟　　　满分：120分)‎ 分数：__________‎ 1‎ ‎ ‎ 第Ⅰ卷　(选择题　共30分)‎ 一、选择题(每小题3分，共30分)‎ ‎1．下列交通标志中，是轴对称图形的是(　B　)‎ ‎2．下列各组数可能是一个三角形的三边长的是(　C　)‎ A．2，4，7 B．5，6，11‎ C．3，4，6 D．4，4，9‎ ‎3．一副三角板有两个三角形，如图叠放在一起，则∠α的度数是(　D　)‎ A．120° B．135° C．150° D．165°‎ ‎　 ‎ 第3题图　　 　第4题图 ‎4．如图，在△ABC中，AD是BC边上的高，BE平分∠ABC交AC边于点E，∠BAC＝60°，∠ABE＝25°，则∠DAC的大小是(　B　)‎ A．15° B．20°‎ C．25° D．30°‎ ‎5．如图，在△ABD和△ACE中，AB＝AC，AD＝AE，要证△ABD≌△ACE，需补充的条件是(　C　)‎ 10‎ ‎ ‎ A．∠B＝∠C B．∠D＝∠E C．∠DAE＝∠BAC D．∠CAD＝∠DAC ‎6．一个多边形的每个外角都等于36°，则这个多边形的边数为(　C　)‎ A．8 B．9 C．10 D．11‎ ‎7．如图，在△ABC中，BC＝8，AB的垂直平分线DH交BC于点D，AC的垂直平分线EF交BC于点E，则△ADE的周长等于(　B　)‎ A．10 B．8 C．6 D．4‎ ‎ ‎ 第7题图　　 第8题图 ‎8．如图，在△ABC中，AC＝2，∠BAC＝75°，∠ACB＝60°，高BE与AD相交于点H，则DH的长为(　D　)‎ A．4 B．3 C．2 D．1‎ ‎9．★如图，在平面直角坐标系中，点A(2，2)在第一象限，点P在x轴上，若以P，O，A为顶点的三角形是等腰三角形，则满足条件的点P共有(　C　)‎ A．2个 B．3个 C．4个 D．5个 ‎ ‎ 第9题图　　　 　　第10题图 ‎10．★如图，△ABC是等边三角形，AQ＝PQ，PR⊥AB于点R，PS⊥AC于点S，PR＝‎ 10‎ ‎ ‎ PS，则下列结论：①点P在∠A的平分线上；②AS＝AR；③QP∥AR；④△BRP≌△QSP.其中正确的有(　D　)‎ A．1个 B．2个 C．3个 D．4个 第Ⅱ卷　(非选择题　共90分)‎ 二、填空题(每小题3分，共24分)‎ ‎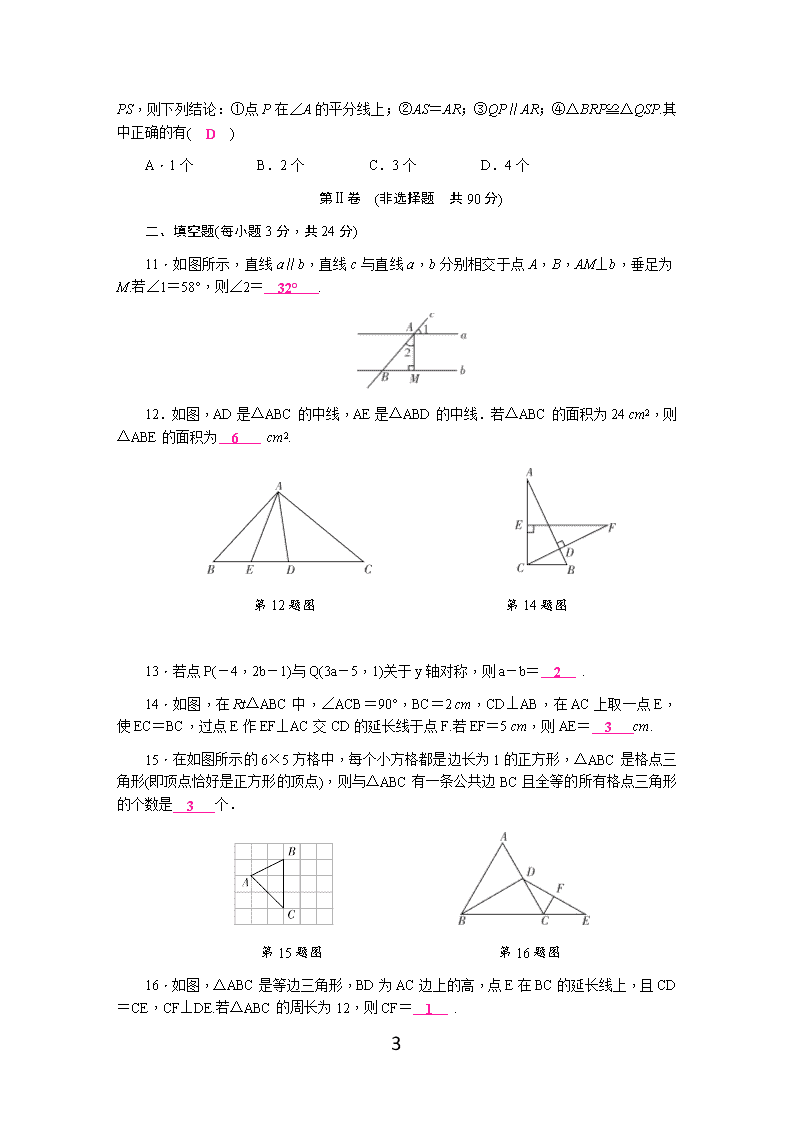11．如图所示，直线a∥b，直线c与直线a，b分别相交于点A，B，AM⊥b，垂足为M.若∠1＝58°，则∠2＝ 32° .‎ ‎12．如图，AD是△ABC的中线，AE是△ABD的中线．若△ABC的面积为24 cm2，则△ABE的面积为 6 cm2.‎ ‎ ‎ 第12题图　　　 第14题图　‎ ‎13．若点P(－4，2b－1)与Q(3a－5，1)关于y轴对称，则a－b＝ 2 .‎ ‎14．如图，在Rt△ABC中，∠ACB＝90°，BC＝2 cm，CD⊥AB，在AC上取一点E，使EC＝BC，过点E作EF⊥AC交CD的延长线于点F.若EF＝5 cm，则AE＝ 3 cm.‎ ‎15．在如图所示的6×5方格中，每个小方格都是边长为1的正方形，△ABC是格点三角形(即顶点恰好是正方形的顶点)，则与△ABC有一条公共边BC且全等的所有格点三角形的个数是 3 个．‎ ‎ ‎ 第15题图　　　 　第16题图 ‎16．如图，△ABC是等边三角形，BD为AC边上的高，点E在BC的延长线上，且CD＝CE，CF⊥DE.若△ABC的周长为12，则CF＝ 1 .‎ 10‎ ‎ ‎ ‎17．★如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，BO，CO分别平分∠ABC，∠ACB，EO∥AB，FO∥AC.若S△ABC＝32，则△OEF的周长为 8 .‎ ‎ ‎ 第17题图　　 　第18题图 ‎18．★如图，点B是线段AC的中点，过点C的射线CE与AC成60°的角，点P为射线CE上一动点，给出以下四个结论：‎ ‎①当AP⊥CE，垂足为P时，∠APB＝30°；‎ ‎②当CP＝AC时，∠APB＝30°；‎ ‎③在射线CE上，使△APC为直角三角形的点P只有1个；‎ ‎④在射线CE上，使△APC为等腰三角形的点P只有1个．‎ 其中正确结论的序号是 ①②④ .‎ 选择、填空题答题卡 一、选择题(每小题3分，共30分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 得分 答案 B C D B C 题号 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 C B D C D 二、填空题(每小题3分，共24分)得分：______‎ ‎11． 32° 　12. 6 　13. 2 ‎ ‎14. 3 15. 3 16. 1　‎ ‎17． 8 18. ①②④ ‎ 10‎ ‎ ‎ 三、解答题(共66分)‎ ‎19．(7分)如图，在△ABC中．‎ ‎(1)画出BC边上的高AD和中线AE；‎ ‎(2)若∠B＝30°，∠ACB＝130°，‎ 求∠BAD和∠CAD的度数．‎ 解：(1)画图如图所示．‎ ‎(2)∠BAC＝180°－130°－30°＝20°.‎ 在Rt△BAD中，‎ ‎∠BAD＝90°－30°＝60°.‎ ‎∠CAD＝60°－20°＝40°.‎ ‎20．(7分)如图，∠ACB＝∠CFE＝90°，AB＝DE，BC＝EF，求证：AD＝CF.‎ 证明：∵∠ACB＝∠CFE＝90°，‎ ‎∴∠ACB＝∠DFE＝90°，‎ 在Rt△ACB和Rt△DFE中，‎ ‎∴Rt△ACB≌Rt△DFE(HL)．‎ ‎∴AC＝DF.‎ ‎∴AC－AF＝DF－AF，即AD＝CF.‎ ‎21．(8分)如图所示，在△ABC中，∠B＝∠C，FD⊥BC，DE⊥AB，垂足分别为D，E，∠AFD＝158°，求∠EDF的度数．‎ 10‎ ‎ ‎ 解：∵∠AFD＝158°，‎ ‎∴∠DFC＝180°－∠AFD＝22°.‎ ‎∵FD⊥BC，‎ ‎∴∠FDC＝90°，‎ ‎∠DFC＋∠C＝90°.‎ ‎∵DE⊥AB，‎ ‎∴∠B＋∠BDE＝90°.‎ ‎∵∠B＝∠C，‎ ‎∴∠BDE＝∠DFC＝22°，‎ ‎∴∠EDF＝180°－∠FDC－∠BDE＝68°.‎ ‎22．(10分)如图所示，△ABC为等边三角形，P为BC边上一点，△APQ为等边三角形．‎ ‎(1)求证：AB∥CQ；‎ ‎(2)是否存在点P，使得AQ⊥CQ？若存在，指出点P的位置；若不存在，请说明理由．‎ ‎(1)证明：∵△ABC，△APQ均为等边三角形，‎ ‎∴AB＝AC，AP＝AQ，‎ ‎∠BAC＝∠PAQ＝‎ ‎∠B＝60°，‎ ‎∴∠BAP＝∠CAQ，‎ ‎∴△ABP≌△ACQ(SAS)．‎ 10‎ ‎ ‎ ‎∴∠ACQ＝∠B＝60°，‎ ‎∴∠ACQ＝∠BAC，∴AB∥CQ.‎ ‎(2)解：当点P为BC的中点时，AQ⊥CQ.理由：‎ ‎∵△ABC为等边三角形，点P为BC的中点，‎ ‎∴∠CAP＝30°.‎ ‎∵△APQ为等边三角形，‎ ‎∴∠CAQ＝30°.‎ 由(1)知∠ACQ＝60°，‎ ‎∴∠AQC＝90°，即AQ⊥CQ.‎ ‎23．(10分)如图，在△ABC中，AB＝AC，点D，E，F分别在AB，BC，AC边上，且BE＝CF，AD＋EC＝AB.‎ ‎(1)求证：△DEF是等腰三角形；‎ ‎(2)当∠A＝40°时，求∠DEF的度数．‎ ‎(1)证明：∵AD＋EC＝AB，‎ AD＋BD＝AB，‎ ‎∴EC＝BD.‎ ‎∵AB＝AC，∴∠B＝∠C，‎ ‎∴△BDE≌△CEF(SAS)，‎ ‎∴DE＝EF，‎ ‎∴△DEF是等腰三角形．‎ ‎(2)解：∵∠A＝40°，∴∠B＝∠C＝70°.‎ ‎∵△BDE≌△CEF，∴∠BDE＝∠CEF.‎ ‎∵∠DEC＝∠B＋∠BDE，‎ ‎∴∠DEF＋∠CEF＝∠B＋∠BDE，‎ 10‎ ‎ ‎ ‎∴∠DEF＝∠B＝70°.‎ ‎24．(12分)如图所示，CE⊥AB，BF⊥AC，BF交CE于点D，且BD＝CD.‎ ‎(1)求证：点D在∠BAC的平分线上；‎ ‎(2)若将条件“BD＝CD”与结论“点D在∠BAC的平分线上”互换，还成立吗？试说明理由．‎ ‎(1)证明：∵CE⊥AB，‎ BF⊥AC，‎ ‎∴∠DEB＝∠DFC＝90°.‎ 在△DEB和△DFC中， ‎∴△DEB≌△DFC(AAS)，‎ ‎∴DE＝DF，∴点D在∠BAC的平分线上．‎ ‎(2)解：将条件“BD＝CD”与结论“点D在∠BAC的平分线上”互换仍然成立，理由如下：‎ ‎∵CE⊥AB，BF⊥AC，‎ ‎∴∠DEB＝∠DFC＝90°.‎ ‎∵点D在∠BAC的平分线上，‎ ‎∴DE＝DF.‎ 在△DEB与△DFC中， ‎∴△DEB≌△DFC(ASA)，‎ ‎∴BD＝CD.‎ 故将条件“BD＝CD”与结论“点D在∠BAC的平分线上”互换仍然成立．‎ ‎25．(12分)在等腰直角三角形ABC中，∠BAC＝90°，点A，点B分别是y轴，x轴上两个动点，直角边AC交x轴于点D，斜边BC交y轴于点E.‎ 10‎ ‎ ‎ ‎(1)如图①，若A(0，1)，B(2，0)，求点C的坐标；‎ ‎(2)如图②，当等腰直角三角形ABC运动到使点D恰为AC中点时，连接DE，求证：∠ADB＝∠CDE；‎ ‎(1)解：过点C作CF⊥y轴于点F.‎ 易证△ACF≌△BAO(AAS)，‎ ‎∴CF＝OA＝1，AF＝OB＝2，‎ ‎∴OF＝1，‎ ‎∴C(－1，－1)．‎ ‎(2)证明：过点C作CG⊥AC交y轴于点G.‎ 易证△ACG≌△BAD(ASA)，‎ ‎∴CG＝AD＝CD，∠ADB＝∠CGE.‎ 由∠DCE＝∠GCE＝45°，‎ 可证△DCE≌△GCE(SAS)．‎ ‎∴∠CDE＝∠CGE，‎ ‎∴∠ADB＝∠CDE.‎ ‎(3)如图③，在等腰直角三角形ABC不断运动的过程中，若满足BD始终是∠ABC的平分线，试探究：线段OA，OD，BD三者之间是否存在某一固定的数量关系，并说明理由．‎ ‎(3)BD＝2OA＋2OD.理由如下：‎ 在OB上截取OH＝OD，连接AH.‎ ‎∴AD＝AH，∠ADH＝∠AHD.‎ ‎∵∠ADH＝∠BAO，‎ 10‎ ‎ ‎ ‎∴∠BAO＝∠AHD.‎ ‎∵BD平分∠ABC，‎ ‎∴∠ABO＝∠EBO.‎ ‎∵∠AOB＝∠EOB＝90°，‎ ‎∴易证△AOB≌△EOB(ASA)，‎ ‎∴AB＝EB，AO＝OE，‎ ‎∴∠BAO＝∠BEO.‎ ‎∴∠AHD＝∠ADH＝∠BAO＝∠BEO，‎ ‎∴∠AEC＝∠BHA.‎ ‎∵AB＝AC，∠CAE＝∠ABH，‎ ‎∴△ACE≌△BAH(AAS)，‎ ‎∴AE＝BH＝2OA.‎ ‎∵DH＝2OD，‎ ‎∴BD＝BH＋DH＝2OA＋2OD. ‎ 10‎