2021人教版八年级上册数学期末测试卷及答案（三套） 54页

八年级数学期末质量检测试卷（一） 一、选择题（本题共 10 小题，每小题 4 分，满分 40 分） 1．（4 分）已知点 P（0，m）在 y 轴的负半轴上，则点 M（﹣m，1）在（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 2．（4 分）已知三角形两边的长分别是 3 和 7，则此三角形第三边的长可能是（ ） A．16 B．11 C．3 D．6 3．（4 分）已知 P1（﹣3，y1），P2（2，y2）是一次函数 y＝2x+1 的图象上的两个点，则 y1，y2 的大小关系是（ ） A．y1＞y2 B．y1＜y2 C．y1＝y2 D．不能确定 4．（4 分）函数 的自变量 x 的取值范围是（ ） A．x＞3 B．x≥3 C．x＜3 D．x≤3 5．（4 分）下面四个图形分别是低碳、节水、节能和绿色食品标志，在这四个标志中， 是轴对称图形的是（ ） A． B． C． D． 6．（4 分）一次函数 y＝kx+k 的图象可能是（ ） A． B． C． D． 7．（4 分）“等腰三角形两底角相等”的逆命题是（ ） A．等腰三角形“三线合一” B．底边上高和中线重合的三角形等腰 C．两个角互余的三角形是等腰三角形 D．有两个角相等的三角形是等腰三角形 8．（4 分）已知图中的两个三角形全等，则∠1 等于（ ） A．50° B．58° C．60° D．72° 9．（4 分）如图，Rt△ABC 中，∠C＝90°，AD 平分∠BAC，交 BC 于点 D，AB＝10， S△ABD＝15，则 CD 的长为（ ） A．3 B．4 C．5 D．6 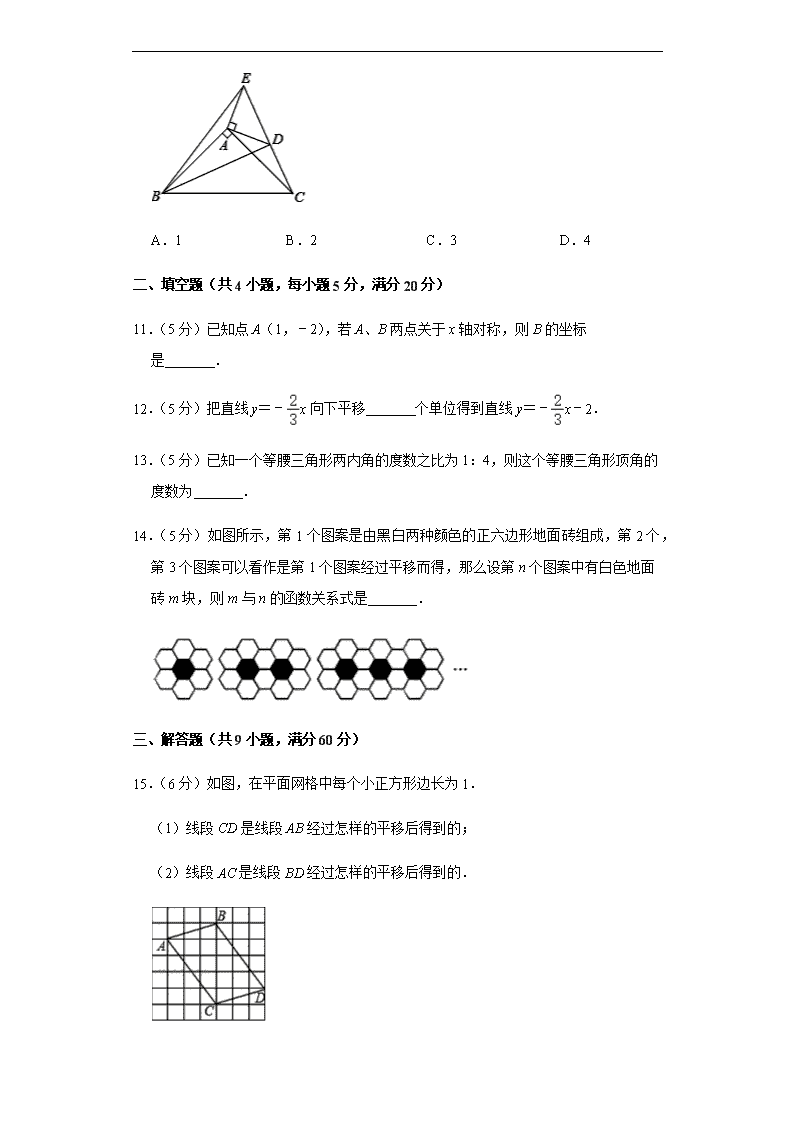10．（4 分）已知：如图，在△ABC，△ADE 中，∠BAC＝∠DAE＝90°，AB＝AC，AD ＝AE，点 C，D，E 三点在同一条直线上，连接 BD，BE．以下四个结论： ① BD＝CE； ② ∠ACE+∠DBC＝45°； ③ BD⊥CE； ④ ∠BAE+∠DAC＝180°． 其中结论正确的个数是（ ） A．1 B．2 C．3 D．4 二、填空题（共 4 小题，每小题 5 分，满分 20 分） 11．（5 分）已知点 A（1，﹣2），若 A、B 两点关于 x 轴对称，则 B 的坐标是 ． 12．（5 分）把直线 y＝﹣ x 向下平移 个单位得到直线 y＝﹣ x﹣2． 13．（5 分）已知一个等腰三角形两内角的度数之比为 1：4，则这个等腰三角形顶角的 度数为 ． 14．（5 分）如图所示，第 1 个图案是由黑白两种颜色的正六边形地面砖组成，第 2 个， 第 3 个图案可以看作是第 1 个图案经过平移而得，那么设第 n 个图案中有白色地面 砖 m 块，则 m 与 n 的函数关系式是 ． 三、解答题（共 9 小题，满分 60 分） 15．（6 分）如图，在平面网格中每个小正方形边长为 1． （1）线段 CD 是线段 AB 经过怎样的平移后得到的； （2）线段 AC 是线段 BD 经过怎样的平移后得到的． 16．（6 分）正比例函数 y＝2x 的图象与一次函数 y＝﹣3x+k 的图象交于点 P（1，m）， 求： （1）k 的值； （2）两条直线与 x 轴围成的三角形的面积． 17．（6 分）已知：如图，CE⊥AB，BF⊥AC，CE 与 BF 相交于 D，且 BD＝CD．求证： ∠BAD＝∠CAD． 18．（6 分）如图，△ABC≌△ADE，且∠CAD＝10°，∠B＝∠D＝25°，∠EAB＝120°， 求∠DFB 和∠DGB 的度数． 19．（7 分）如图，在等边△ABC 中，点 D，E 分別在边 BC，AC 上，DE∥AB，过点 E 作 EF⊥DE，交 BC 的延长线于点 F． （1）求∠F 的度数； （2）若 CD＝2，求 DF、EF 的长． 20．（7 分）如图，直线 l1：y1＝x 和直线 l2：y2＝﹣2x+6 相交于点 A，直线 l2 与 x 轴交 于点 B，动点 P 沿路线 O→A→B 运动． （1）求点 A 的坐标，并回答当 x 取何值时 y1＞y2？ （2）求△AOB 的面积； （3）当△POB 的面积是△AOB 的面积的一半时，求出这时点 P 的坐标． 21．（7 分）如图所示，在△ABC 中，∠A＝40°，∠B＝90°，AC 的垂直平分线 MN 分别与 AB、AC 交于点 D、E，求∠BCD 的度数． 22．（7 分）如图，在△ABD 和△ACE 中，有四个等式： ① AB＝AC； ② AD＝AE； ③ ∠ 1＝∠2； ④ BD＝CE，请你从其中三个等式作为题设，设另一个作为结论，写出一个 真命题，并给出证明．（要求写出已知、求证及证明过程） 23．（8 分）已知：点 O 到△ABC 的两边 AB，AC 所在直线的距离相等，且 OB＝OC． （1）如图 1，若点 O 在边 BC 上，求证：AB＝AC； （2）如图 2，若点 O 在△ABC 的内部，求证：AB＝AC； （3）若点 O 在△ABC 的外部，AB＝AC 成立吗？请画出图表示． 参考答案与试题解析 一、选择题（本题共 10 小题，每小题 4 分，满分 40 分） 1．（4 分）已知点 P（0，m）在 y 轴的负半轴上，则点 M（﹣m，1）在（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 【解答】解：∵点 P（0，m）在 y 轴的负半轴上， ∴m＜0， ∴﹣m＞0， ∴点 M（﹣m，1）在第一象限， 故选：A． 2．（4 分）已知三角形两边的长分别是 3 和 7，则此三角形第三边的长可能是（ ） A．16 B．11 C．3 D．6 【解答】解：设第三边的长度为 x， 由题意得：7﹣3＜x＜7+3， 即：4＜x＜10， 故选：D． 3．（4 分）已知 P1（﹣3，y1），P2（2，y2）是一次函数 y＝2x+1 的图象上的两个点，则 y1，y2 的大小关系是（ ） A．y1＞y2 B．y1＜y2 C．y1＝y2 D．不能确定 【解答】解：∵一次函数 y＝2x+1 中 k＝2＞0， ∴此函数是增函数， ∵﹣3＜2， ∴y1＜y2． 故选：B． 4．（4 分）函数 的自变量 x 的取值范围是（ ） A．x＞3 B．x≥3 C．x＜3 D．x≤3 【解答】解：根据题意得：3﹣x≥0， 解得 x≤3． 故选：D． 5．（4 分）下面四个图形分别是低碳、节水、节能和绿色食品标志，在这四个标志中， 是轴对称图形的是（ ） A． B． C． D． 【解答】解：A、不是轴对称图形，故此选项错误； B、不是轴对称图形，故此选项错误； C、不是轴对称图形，故此选项错误； D、是轴对称图形，故此选项正确； 故选：D． 6．（4 分）一次函数 y＝kx+k 的图象可能是（ ） A． B． C． D． 【解答】解：当 k＞0 时，函数图象经过一、二、三象限； 当 k＜0 时，函数图象经过二、三、四象限，故 B 正确． 故选：B． 7．（4 分）“等腰三角形两底角相等”的逆命题是（ ） A．等腰三角形“三线合一” B．底边上高和中线重合的三角形等腰 C．两个角互余的三角形是等腰三角形 D．有两个角相等的三角形是等腰三角形 【解答】解：“等腰三角形两底角相等”的逆命题是有两个角相等的三角形是等腰三 角形，故选 D． 8．（4 分）已知图中的两个三角形全等，则∠1 等于（ ） A．50° B．58° C．60° D．72° 【解答】解： ∵△ABC 和△DEF 全等，AC＝DF＝b，DE＝AB＝a， ∴∠1＝∠B，∠A＝∠D＝50°，∠F＝∠C＝72°， ∴∠1＝180°﹣∠D﹣∠F＝58°， 故选：B． 9．（4 分）如图，Rt△ABC 中，∠C＝90°，AD 平分∠BAC，交 BC 于点 D，AB＝10， S△ABD＝15，则 CD 的长为（ ） A．3 B．4 C．5 D．6 【解答】解：如图，过点 D 作 DE⊥AB 于 E， ∵∠C＝90°，AD 平分∠BAC， ∴DE＝CD， ∴S△ABD＝ AB•DE＝ ×10•DE＝15， 解得 DE＝3， ∴CD＝3． 故选：A． 10．（4 分）已知：如图，在△ABC，△ADE 中，∠BAC＝∠DAE＝90°，AB＝AC，AD ＝AE，点 C，D，E 三点在同一条直线上，连接 BD，BE．以下四个结论： ① BD＝CE； ② ∠ACE+∠DBC＝45°； ③ BD⊥CE； ④ ∠BAE+∠DAC＝180°． 其中结论正确的个数是（ ） A．1 B．2 C．3 D．4 【解答】解： ① ∵∠BAC＝∠DAE＝90°， ∴∠BAC+∠CAD＝∠DAE+∠CAD，即∠BAD＝∠CAE， ∵在△BAD 和△CAE 中， ， ∴△BAD≌△CAE（SAS）， ∴BD＝CE，本选项正确； ② ∵△ABC 为等腰直角三角形， ∴∠ABC＝∠ACB＝45°， ∴∠ABD+∠DBC＝45°， ∵△BAD≌△CAE， ∴∠ABD＝∠ACE， ∴∠ACE+∠DBC＝45°，本选项正确； ③ ∵∠ABD+∠DBC＝45°， ∴∠ACE+∠DBC＝45°， ∴∠DBC+∠DCB＝∠DBC+∠ACE+∠ACB＝90°， 则 BD⊥CE，本选项正确； ④ ∵∠BAC＝∠DAE＝90°， ∴∠BAE+∠DAC＝360°﹣90°﹣90°＝180°，故此选项正确， 故选：D． 二、填空题（共 4 小题，每小题 5 分，满分 20 分） 11．（5 分）已知点 A（1，﹣2），若 A、B 两点关于 x 轴对称，则 B 的坐标是 （1，2） ． 【解答】解：∵A、B 两点关于 x 轴对称， ∴点 B 的坐标是（1，2）． 故答案为：（1，2）． 12．（5 分）把直线 y＝﹣ x 向下平移 2 个单位得到直线 y＝﹣ x﹣2． 【解答】解：∵0﹣（﹣2）＝2， ∴根据“上加下减”的原则可知，把直线 y＝﹣ x 向下平移 2 个单位得到直线 y＝ ﹣ x﹣2． 故答案为：2． 13．（5 分）已知一个等腰三角形两内角的度数之比为 1：4，则这个等腰三角形顶角的 度数为 120°或 20° ． 【解答】解：设两个角分别是 x，4x ① 当 x 是底角时，根据三角形的内角和定理，得 x+x+4x＝180°，解得，x＝30°， 4x＝120°，即底角为 30°，顶角为 120°； ② 当 x 是顶角时，则 x+4x+4x＝180°，解得，x＝20°，从而得到顶角为 20°，底 角为 80°； 所以该三角形的顶角为 120°或 20°． 故答案为：120°或 20°． 14．（5 分）如图所示，第 1 个图案是由黑白两种颜色的正六边形地面砖组成，第 2 个， 第 3 个图案可以看作是第 1 个图案经过平移而得，那么设第 n 个图案中有白色地面 砖 m 块，则 m 与 n 的函数关系式是 m＝4n+2 ． 【解答】解：首先发现：第一个图案中，有白色的是 6 个，后边是依次多 4 个． 所以第 n 个图案中，是 6+4（n﹣1）＝4n+2． ∴m 与 n 的函数关系式是 m＝4n+2． 故答案为：4n+2． 三、解答题（共 9 小题，满分 60 分） 15．（6 分）如图，在平面网格中每个小正方形边长为 1． （1）线段 CD 是线段 AB 经过怎样的平移后得到的； （2）线段 AC 是线段 BD 经过怎样的平移后得到的． 【解答】解：（1）将线段 AB 向右（或下）平移 3 个小格（或 4 个小格），再向下（或 右）平移 4 个小格（或 3 个小格），得线段 CD． （2）将线段 BD 向右平移（或向下平移 1 个小格）3 个小格，再向下平移（可左平 移 3 个小格）1 个小格，得到线段 AC． 16．（6 分）正比例函数 y＝2x 的图象与一次函数 y＝﹣3x+k 的图象交于点 P（1，m）， 求： （1）k 的值； （2）两条直线与 x 轴围成的三角形的面积． 【解答】解：（1）∵正比例函数 y＝2x 的图象与一次函数 y＝﹣3x+k 的图象交于点 P （1，m）， ∴把点 P（1，m）代入得： ， 把 ① 代入 ② 得：k＝5； （2）根据题意，如图： ∵点 P（1，2）， ∴三角形的高就是 2， ∵y＝﹣3x+5， ∴A（0， ）， ∴OA＝ ， ∴S△AOP＝ × ×2＝ 17．（6 分）已知：如图，CE⊥AB，BF⊥AC，CE 与 BF 相交于 D，且 BD＝CD．求证： ∠BAD＝∠CAD． 【解答】证明：∵CE⊥AB，BF⊥AC， ∴∠BED＝∠CFD＝90°， 在△BED 和△CFD 中， ， ∴△BED≌△CFD（AAS）， ∴DE＝DF， ∵CE⊥AB，BF⊥AC， ∴∠BAD＝∠CAD． 18．（6 分）如图，△ABC≌△ADE，且∠CAD＝10°，∠B＝∠D＝25°，∠EAB＝120°， 求∠DFB 和∠DGB 的度数． 【解答】解：∵△ABC≌△ADE， ∴∠DAE＝∠BAC＝ （∠EAB﹣∠CAD）＝ ． ∴∠DFB＝∠FAB+∠B＝∠FAC+∠CAB+∠B＝10°+55°+25°＝90° ∠DGB＝∠DFB﹣∠D＝90°﹣25°＝65°． 综上所述：∠DFB＝90°，∠DGB＝65°． 19．（7 分）如图，在等边△ABC 中，点 D，E 分別在边 BC，AC 上，DE∥AB，过点 E 作 EF⊥DE，交 BC 的延长线于点 F． （1）求∠F 的度数； （2）若 CD＝2，求 DF、EF 的长． 【解答】解：（1）∵△ABC 是等边三角形， ∴∠B＝60°， ∵DE∥AB， ∴∠EDC＝∠B＝60°， ∵EF⊥DE， ∴∠DEF＝90°， ∴∠F＝90°﹣∠EDC＝30°； （2）∵∠ACB＝60°，∠EDC＝60°， ∴△EDC 是等边三角形． ∴ED＝DC＝2， ∵∠DEF＝90°，∠F＝30°， ∴DF＝2DE＝4， ∴EF＝ DE＝2 ． 20．（7 分）如图，直线 l1：y1＝x 和直线 l2：y2＝﹣2x+6 相交于点 A，直线 l2 与 x 轴交 于点 B，动点 P 沿路线 O→A→B 运动． （1）求点 A 的坐标，并回答当 x 取何值时 y1＞y2？ （2）求△AOB 的面积； （3）当△POB 的面积是△AOB 的面积的一半时，求出这时点 P 的坐标． 【解答】解：（1）∵直线 l1 与直线 l2 相交于点 A， ∴y1＝y2，即﹣2x+6＝x，解得 x＝2， ∴y1＝y2＝2， ∴点 A 的坐标为（2，2）； 观察图象可得，当 x＞2 时，y1＞y2； （2）由直线 l2：y2＝﹣2x+6 可知，当 y＝0 时，x＝3， ∴B（3，0）， ∴S△AOB＝ ×3×2＝3； （3）∵△POB 的面积是△AOB 的面积的一半， ∴P 的纵坐标为 1， ∵点 P 沿路线 O→A→B 运动， ∴P（1，1）或（ ，1）． 21．（7 分）如图所示，在△ABC 中，∠A＝40°，∠B＝90°，AC 的垂直平分线 MN 分别与 AB、AC 交于点 D、E，求∠BCD 的度数． 【解答】解：∵∠B＝90°，∠A＝40°， ∴∠ACB＝50°， ∵MN 是线段 AC 的垂直平分线． ∴AE＝CE． 在△ADE 和△CDE 中， . ． ∴△ADE≌△CDE（SAS） ∴∠DCA＝∠A＝40° ∴∠BCD＝∠ACB﹣∠DCA ＝50°﹣40° ＝10°． 22．（7 分）如图，在△ABD 和△ACE 中，有四个等式： ① AB＝AC； ② AD＝AE； ③ ∠ 1＝∠2； ④ BD＝CE，请你从其中三个等式作为题设，设另一个作为结论，写出一个 真命题，并给出证明．（要求写出已知、求证及证明过程） 【解答】解：解法一：如果 AB＝AC，AD＝AE，BD＝CE，那么∠1＝∠2． 已知：在△ABD 和△ACE 中，AB＝AC，AD＝AE，BD＝CE， 求证：∠1＝∠2． 证明：在△ABD 和△ACE 中， ， ∴△ABD≌△ACE， ∴∠BAD＝∠CAE， ∴∠1＝∠2． 解法二：如果 AB＝AC，AD＝AE，∠1＝∠2，那么 BD＝CE． 已知：在△ABD 和△ACE 中，AB＝AC，AD＝AE，∠1＝∠2， 求证：BD＝CE． 证明：∵∠1＝∠2， ∴∠BAD＝∠CAE． 在△ABD 和△ACE 中， ， ∴△ABD≌△ACE， ∴BD＝CE． 23．（8 分）已知：点 O 到△ABC 的两边 AB，AC 所在直线的距离相等，且 OB＝OC． （1）如图 1，若点 O 在边 BC 上，求证：AB＝AC； （2）如图 2，若点 O 在△ABC 的内部，求证：AB＝AC； （3）若点 O 在△ABC 的外部，AB＝AC 成立吗？请画出图表示． 【解答】（1）证明：过点 O 分别作 OE⊥AB 于 E，OF⊥AC 于 F， 由题意知， 在 Rt△OEB 和 Rt△OFC 中 ∴Rt△OEB≌Rt△OFC（HL）， ∴∠ABC＝∠ACB， ∴AB＝AC； （2）证明：过点 O 分别作 OE⊥AB 于 E，OF⊥AC 于 F， 由题意知，OE＝OF．∠BEO＝∠CFO＝90°， ∵在 Rt△OEB 和 Rt△OFC 中 ∴Rt△OEB≌Rt△OFC（HL）， ∴∠OBE＝∠OCF， 又∵OB＝OC， ∴∠OBC＝∠OCB， ∴∠ABC＝∠ACB， ∴AB＝AC； （3）解：不一定成立，当∠A 的平分线所在直线与边 BC 的垂直平分线重合时 AB＝ AC，否则 AB≠AC．（如示例图） 八年级数学期末质量检测试卷（二） 一、选择题（本大题共 10 小题，每小题 3 分，共 30 分） 1．（3 分）下列四个图案中，不是轴对称图案的是（ ） A． B． C． D． 2．（3 分）已知点 A 的坐标为（﹣2，3），则点 A 关于 y 轴的对称点的坐标是（ ） A．（﹣2，3） B．（2，3） C．（2，﹣3） D．（﹣2，﹣3） 3．（3 分）下列运算正确的是（ ） A． ＝±4 B．（ab2）3＝a3b6 C．a6÷a2＝a3 D．（a﹣b）2＝a2﹣b2 4．（3 分）若 x2+mxy+4y2 是一个完全平方式，那么 m 的值是（ ） A．±4 B．﹣2 C．±2 D．4 5．（3 分）若 3x＝4，9y＝7，则 3x﹣2y 的值为（ ） A． B． C．﹣3 D． 6．（3 分）如图 1，在边长为 a 的正方形中挖掉一个边长为 b 的小正方形（a＞b），把余 下的部分剪拼成如图 2 所示的长方形．通过计算剪拼前后阴影部分的面积，验证了 一个等式，这则个等式是（ ） A．（a+b）（a﹣b）＝a2﹣b2 B．（a+b）2＝a2+2ab+b2 C．（a﹣b）2＝a2﹣2ab+b2 D．a（a﹣b）＝a2﹣ab 7．（3 分）如图，已知∠ACB＝∠DBC，添加以下条件，不能判定△ABC≌△DCB 的是 （ ） A．∠ABC＝∠DCB B．∠ABD＝∠DCA C．AC＝DB D．AB＝DC 8．（3 分）如图，在△ABC 中，AB＝AC，AD、CE 是△ABC 的两条中线，点 P 是 AD 上一个动点，则 BP+EP 的最小值等于线段（ ）的长度． A．BC B．CE C．AD D．AC 9．（3 分）如图，在△ABC 中，AB＝AC，BE＝CD，BD＝CF，则∠EDF 的度数为（ ） A．45° ∠A B．90 ∠A C．90°﹣∠A D．180°﹣∠A 10．（3 分）如图，△ABC 为等边三角形，AE＝CD，AD、BE 相交于点 P，BQ⊥AD 于 Q，PQ＝3，PE＝1．AD 的长是（ ） A．5 B．6 C．7 D．8 二、填空题（本大题共 6 小题，每小题 3 分，共 18 分） 11．（3 分）因式分解：a2b﹣4ab+4b＝ ． 12．（3 分）要使代数式 有意义，则 x 的取值范围是 ． 13．（3 分）若 a﹣b＝1，ab＝2，那么 a+b 的值为 ． 14．（3 分）如图所示，将△ABC 沿着 DE 翻折，若∠1+∠2＝80°，则∠B＝ 度． 15．（3 分）繁昌到南京大约 150 千米，由于开通了高铁，动车的的平均速度是汽车的 2.5 倍，这样乘动车到南京比坐汽车就要节省 1.2 小时，设汽车的平均速度为 x 千米/ 时，根据题意列出方程 ． 16．（3 分）如图，在△ABC 中，AB＝AC，∠BAC＝90°，直角∠EPF 的顶点 P 是 BC 的中点，两边 PE，PF 分别交 AB，AC 于点 E，F，连接 EF 交 AP 于点 G．给出以下 四个结论，其中正确的结论是 ． ① AE＝CF， ② AP＝EF， ③ △EPF 是等腰直角三角形， ④ 四边形 AEPF 的面积是△ABC 面积的一半． 三、解答题（本大题共 7 小题，共 52 分.解答应写明文字说明和运算步骤） 17．（10 分）计算 （1）4（a﹣b）2﹣（2a+b）（2a﹣b）． （2）先化简，再求值（a+2﹣ ）÷ ，其中 a＝1 18．（6 分）给出下列等式：21﹣20＝20，22﹣21＝21，23﹣22＝22，24﹣23＝23，…… （1）探索上面式子的规律，试写出第 n 个等式，并证明其成立． （2）运用上述规律计算 20+21+22+…+22017+22018 值． 19．（6 分）如图，在 Rt△ABC 中，∠ACB＝90°，CD 是 AB 边上的高， （1）尺规作图：作△ABC 的角平分线 AE，交 CD 于点 F（不写作法，保留作图痕迹）； （2）求证：△CEF 为等腰三角形． 20．（6 分）如图，△ABC 三个顶点的坐标分别为 A（1，1），B（4，2），C（3，4）． （1）请画出△ABC 关于 y 轴的对称图形△A1B1C1； （2）在 y 轴上求作一点 P，使△PAC 的周长最小，并直接写出 P 的坐标． 21．（6 分）某县为了落实中央的“强基惠民工程”，计划将某村的居民自来水管道进行 改造．该工程若由甲队单独施工恰好在规定时间内完成；若乙队单独施工，则完成 工程所需天数是规定天数的 1.5 倍．如果由甲、乙队先合做 15 天，那么余下的工程 由甲队单独完成还需 5 天．这项工程的规定时间是多少天？ 22．（8 分）如图，在平面直角坐标系中，等腰直角△ABC，AB⊥BC，AB＝BC，点 C 在第一象限．已知点 A（m，0），B（0，n）（n＞m＞0），点 P 在线段 OB 上，且 OP ＝OA． （1）点 C 的坐标为 （用含 m，n 的式子表示） （2）求证：CP⊥AP． 23．（10 分）如图（1）AC⊥AB，BD⊥AB，AB＝12cm，AC＝BD＝8cm，点 P 在线段 AB 上以 2cm/s 的速度由点 A 向点 B 运动，同时，点 Q 在线段 BD 上由点 B 向点 D 运动，它们运动的时间为 t（s）． （1）若点 Q 的运动速度与点 P 的运动速度相等，当 t＝2 时，△ACP 与△BPQ 是否 全等，请说明理由； （2）在（1）的条件下，判断此时线段 PC 和线段 PQ 的位置关系，并证明； （3）如图（2），将图（1）中的“AC⊥AB，BD⊥AB”改为“∠CAB＝∠DBA＝50°”， 其他条件不变．设点 Q 的运动速度为 xcm/s，是否存在实数 x，使得△ACP 与△BPQ 全等？若存在，求出相应的 x、t 的值；若不存在，请说明理由． 参考答案与试题解析 一、选择题（本大题共 10 小题，每小题 3 分，共 30 分） 1．（3 分）下列四个图案中，不是轴对称图案的是（ ） A． B． C． D． 【解答】解：A．此图案是轴对称图形，不符合题意； B．此图案不是轴对称图形，符合题意； C．此图案是轴对称图形，不符合题意； D．此图案是轴对称图形，不符合题意； 故选：B． 2．（3 分）已知点 A 的坐标为（﹣2，3），则点 A 关于 y 轴的对称点的坐标是（ ） A．（﹣2，3） B．（2，3） C．（2，﹣3） D．（﹣2，﹣3） 【解答】解：∵点 A 的坐标为（﹣2，3）， ∴点 A 关于 y 轴的对称点的坐标是（2，﹣3）， 故选：B． 3．（3 分）下列运算正确的是（ ） A． ＝±4 B．（ab2）3＝a3b6 C．a6÷a2＝a3 D．（a﹣b）2＝a2﹣b2 【解答】解：A. ，故本选项不合题意； B．（ab2）3＝a3b6，正确； C．a6÷a2＝a4，故本选项不合题意； D．（a﹣b）2＝a2﹣2ab+b2，故本选项不合题意． 故选：B． 4．（3 分）若 x2+mxy+4y2 是一个完全平方式，那么 m 的值是（ ） A．±4 B．﹣2 C．±2 D．4 【解答】解：∵x2+mxy+4y2＝x2+mxy+（2y）2， ∴mxy＝±2x•2y， 解得：m＝±4． 故选：A． 5．（3 分）若 3x＝4，9y＝7，则 3x﹣2y 的值为（ ） A． B． C．﹣3 D． 【解答】解：∵3x＝4，9y＝7， ∴3x﹣2y＝3x÷32y＝3x÷（32）y＝4÷7＝ ． 故选：A． 6．（3 分）如图 1，在边长为 a 的正方形中挖掉一个边长为 b 的小正方形（a＞b），把余 下的部分剪拼成如图 2 所示的长方形．通过计算剪拼前后阴影部分的面积，验证了 一个等式，这则个等式是（ ） A．（a+b）（a﹣b）＝a2﹣b2 B．（a+b）2＝a2+2ab+b2 C．（a﹣b）2＝a2﹣2ab+b2 D．a（a﹣b）＝a2﹣ab 【解答】解：图 1 阴影部分面积：a2﹣b2， 图 2 阴影部分面积：（a+b）（a﹣b）， 由此验证了等式（a+b）（a﹣b）＝a2﹣b2， 故选：A． 7．（3 分）如图，已知∠ACB＝∠DBC，添加以下条件，不能判定△ABC≌△DCB 的是 （ ） A．∠ABC＝∠DCB B．∠ABD＝∠DCA C．AC＝DB D．AB＝DC 【解答】解：A、∵在△ABC 和△DCB 中 ∴△ABC≌△DCB（ASA），故本选项不符合题意； B、∵∠ABD＝∠DCA，∠DBC＝∠ACB， ∴∠ABD+∠DBC＝∠ACD+∠ACB， 即∠ABC＝∠DCB， ∵在△ABC 和△DCB 中 ∴△ABC≌△DCB（ASA），故本选项不符合题意； C、∵在△ABC 和△DCB 中 ∴△ABC≌△DCB（SAS），故本选项不符合题意； D、根据∠ACB＝∠DBC，BC＝BC，AB＝DC 不能推出△ABC≌△DCB，故本选项 符合题意； 故选：D． 8．（3 分）如图，在△ABC 中，AB＝AC，AD、CE 是△ABC 的两条中线，点 P 是 AD 上一个动点，则 BP+EP 的最小值等于线段（ ）的长度． A．BC B．CE C．AD D．AC 【解答】解：如图，连接 PC， ∵AB＝AC，BD＝CD， ∴AD⊥BC， ∴PB＝PC， ∴PB+PE＝PC+PE， ∵PE+PC≥CE， ∴P、C、E 共线时，PB+PE 的值最小，最小值为 CE 的长度， 故选：B． 9．（3 分）如图，在△ABC 中，AB＝AC，BE＝CD，BD＝CF，则∠EDF 的度数为（ ） A．45° ∠A B．90 ∠A C．90°﹣∠A D．180°﹣∠A 【解答】解：∵AB＝AC， ∴∠B＝∠C， ∵BD＝CF，BE＝CD ∴△BDE≌△CFD， ∴∠BDE＝∠CFD， ∠EDF＝180°﹣（∠BDE+∠CDF）＝180°﹣（∠CFD+∠CDF）＝180°﹣（180° ﹣∠C）＝∠C， ∵∠A+∠B+∠C＝180°． ∴∠A+2∠EDF＝180°， ∴∠EDF＝90°﹣ ∠A． 故选：B． 10．（3 分）如图，△ABC 为等边三角形，AE＝CD，AD、BE 相交于点 P，BQ⊥AD 于 Q，PQ＝3，PE＝1．AD 的长是（ ） A．5 B．6 C．7 D．8 【解答】解：∵△ABC 为等边三角形， ∴AB＝CA，∠BAE＝∠ACD＝60°； 又∵AE＝CD， 在△ABE 和△CAD 中， ， ∴△ABE≌△CAD（SAS）； ∴BE＝AD，∠CAD＝∠ABE； ∴∠BPQ＝∠ABE+∠BAD＝∠BAD+∠CAD＝∠BAE＝60°； ∵BQ⊥AD， ∴∠AQB＝90°，则∠PBQ＝90°﹣60°＝30°； ∵PQ＝3， ∴在 Rt△BPQ 中，BP＝2PQ＝6； 又∵PE＝1， ∴AD＝BE＝BP+PE＝7． 故选：C． 二、填空题（本大题共 6 小题，每小题 3 分，共 18 分） 11．（3 分）因式分解：a2b﹣4ab+4b＝ b（a﹣2）2 ． 【解答】解：原式＝b（a2﹣4a+4）＝b（a﹣2）2， 故答案为：b（a﹣2）2 12．（3 分）要使代数式 有意义，则 x 的取值范围是 x≥﹣1 且 x≠0 ． 【解答】解：根据题意，得 ， 解得 x≥﹣1 且 x≠0． 13．（3 分）若 a﹣b＝1，ab＝2，那么 a+b 的值为 ±3 ． 【解答】解：把 a﹣b＝1，两边平方得：（a﹣b）2＝a2+b2﹣2ab＝1， 把 ab＝2 代入得：a2+b2＝5， ∴（a+b）2＝a2+b2+2ab＝9， 则 a+b＝±3， 故答案为：±3 14．（3 分）如图所示，将△ABC 沿着 DE 翻折，若∠1+∠2＝80°，则∠B＝ 40 度． 【解答】解：∵△ABC 沿着 DE 翻折， ∴∠1+2∠BED＝180°，∠2+2∠BDE＝180°， ∴∠1+∠2+2（∠BED+∠BDE）＝360°， 而∠1+∠2＝80°，∠B+∠BED+∠BDE＝180°， ∴80°+2（180°﹣∠B）＝360°， ∴∠B＝40°． 故答案为：40°． 15．（3 分）繁昌到南京大约 150 千米，由于开通了高铁，动车的的平均速度是汽车的 2.5 倍，这样乘动车到南京比坐汽车就要节省 1.2 小时，设汽车的平均速度为 x 千米/ 时，根据题意列出方程 ＝ +1.2 ． 【解答】解：设原来火车的平均速度为 x 千米/时，则动车运行后的平均速度为 1.8x， 由题意得， ＝ +1.2． 故答案为： ＝ +1.2． 16．（3 分）如图，在△ABC 中，AB＝AC，∠BAC＝90°，直角∠EPF 的顶点 P 是 BC 的中点，两边 PE，PF 分别交 AB，AC 于点 E，F，连接 EF 交 AP 于点 G．给出以下 四个结论，其中正确的结论是 ①③④ ． ① AE＝CF， ② AP＝EF， ③ △EPF 是等腰直角三角形， ④ 四边形 AEPF 的面积是△ABC 面积的一半． 【解答】解：∵AB＝AC，∠BAC＝90°，直角∠EPF 的顶点 P 是 BC 的中点， ∴∠B＝∠C＝45°，AP⊥BC，AP＝ BC＝PC＝BP，∠BAP＝∠CAP＝45°， ∵∠APF+∠FPC＝90°，∠APF+∠APE＝90°， ∴∠FPC＝∠EPA． ∴△APE≌△CPF（ASA）， ∴AE＝CF；EP＝PF，即△EPF 是等腰直角三角形；故 ①③ 正确； S△AEP＝S△CFP， ∵四边形 AEPF 的面积＝S△AEP+S△APF＝S△CFP+S△APF＝S△APC＝ S△ABC， ∴四边形 AEPF 的面积是△ABC 面积的一半，故 ④ 正确 ∵△ABC 是等腰直角三角形，P 是 BC 的中点， ∴AP＝ BC， ∵EF 不是△ABC 的中位线， ∴EF≠AP，故 ② 错误； 故答案为： ①③④ ． 三、解答题（本大题共 7 小题，共 52 分.解答应写明文字说明和运算步骤） 17．（10 分）计算 （1）4（a﹣b）2﹣（2a+b）（2a﹣b）． （2）先化简，再求值（a+2﹣ ）÷ ，其中 a＝1 【解答】解：（1）原式＝4（a2﹣2ab+b2）﹣（4a2﹣b2） ＝4a2﹣8ab+4b2﹣4a2+b2 ＝﹣8ab+5b2； （2）原式＝（ ﹣ ）÷ ＝ • ＝ • ＝ ， 当 a＝1 时， 原式＝ ＝﹣ ． 18．（6 分）给出下列等式：21﹣20＝20，22﹣21＝21，23﹣22＝22，24﹣23＝23，…… （1）探索上面式子的规律，试写出第 n 个等式，并证明其成立． （2）运用上述规律计算 20+21+22+…+22017+22018 值． 【解答】（1）第 n 个等式是：2n﹣2n﹣1＝2n﹣1， 证明：∵2n﹣2n﹣1 ＝2×2n﹣1﹣2n﹣1 ＝（2﹣1）×2n﹣1 ＝1×2n﹣1 ＝2n﹣1， ∴2n﹣2n﹣1＝2n﹣1 成立； （2）20+21+22+…+22017+22018 ＝（21﹣20）+（22﹣21）+（23﹣22）+…+（22019﹣22018） ＝21﹣20+22﹣21+23﹣22+…+22019﹣22018 ＝﹣20+22019 ＝22019﹣1． 19．（6 分）如图，在 Rt△ABC 中，∠ACB＝90°，CD 是 AB 边上的高， （1）尺规作图：作△ABC 的角平分线 AE，交 CD 于点 F（不写作法，保留作图痕迹）； （2）求证：△CEF 为等腰三角形． 【解答】（1）解：如图线段 AE 即为所求； （2）证明：∵CD⊥AB， ∴∠BDC＝∠ACB＝90°， ∴∠ACD+∠DCB＝90°，∠DCB+∠B＝90°， ∴∠ACD＝∠B， ∵∠CFE＝∠ACF+∠CAF，∠CEF＝∠B+∠EAB，∠CAF＝∠EAB， ∴∠CEF＝∠CFE， ∴CE＝CF， ∴△CEF 是等腰三角形． 20．（6 分）如图，△ABC 三个顶点的坐标分别为 A（1，1），B（4，2），C（3，4）． （1）请画出△ABC 关于 y 轴的对称图形△A1B1C1； （2）在 y 轴上求作一点 P，使△PAC 的周长最小，并直接写出 P 的坐标． 【解答】解：（1）如图所示，△A1B1C1 即为所求； （2）连接 A1C 交 y 轴于 P，连接 AP，则点 P 即为所求． 根据轴对称的性质可得，A1P＝AP， ∵A1P+CP＝A1C（最短）， ∴AP+PC+AC 最短，即△PAC 的周长最小， ∵C（3，4），A1（﹣1，1）， ∴直线 A1C 解析式为 y＝ x+ ， ∴当 x＝0 时，y＝ ， ∴P（0， ）． 21．（6 分）某县为了落实中央的“强基惠民工程”，计划将某村的居民自来水管道进行 改造．该工程若由甲队单独施工恰好在规定时间内完成；若乙队单独施工，则完成 工程所需天数是规定天数的 1.5 倍．如果由甲、乙队先合做 15 天，那么余下的工程 由甲队单独完成还需 5 天．这项工程的规定时间是多少天？ 【解答】解：设这项工程的规定时间是 x 天，根据题意得 ＝1． 解得：x＝30． 经检验 x＝30 是方程的解． 答：这项工程的规定时间是 30 天． 22．（8 分）如图，在平面直角坐标系中，等腰直角△ABC，AB⊥BC，AB＝BC，点 C 在第一象限．已知点 A（m，0），B（0，n）（n＞m＞0），点 P 在线段 OB 上，且 OP ＝OA． （1）点 C 的坐标为 （n，m+n） （用含 m，n 的式子表示） （2）求证：CP⊥AP． 【解答】解：（1）如图，过点 C 作 CD⊥y 轴于点 D， ∴∠CDB＝90°， ∴∠DCB+∠DBC＝90°，且∠ABO+∠CBD＝90°， ∴∠DCB＝∠ABO，且 AB＝BC，∠CDB＝∠AOB＝90°， ∴△CDB≌△BOA（AAS） ∴BO＝CD＝n，AO＝BD＝m， ∴OD＝m+n， ∴点 C（n，m+n）， 故答案为：（n，m+n）； （2）∵OP＝OA＝m，OD＝m+n， ∴DP＝n＝DC，∠OPA＝45°， ∴∠DPC＝45°， ∴∠APC＝90°， ∴AP⊥PC． 23．（10 分）如图（1）AC⊥AB，BD⊥AB，AB＝12cm，AC＝BD＝8cm，点 P 在线段 AB 上以 2cm/s 的速度由点 A 向点 B 运动，同时，点 Q 在线段 BD 上由点 B 向点 D 运动，它们运动的时间为 t（s）． （1）若点 Q 的运动速度与点 P 的运动速度相等，当 t＝2 时，△ACP 与△BPQ 是否 全等，请说明理由； （2）在（1）的条件下，判断此时线段 PC 和线段 PQ 的位置关系，并证明； （3）如图（2），将图（1）中的“AC⊥AB，BD⊥AB”改为“∠CAB＝∠DBA＝50°”， 其他条件不变．设点 Q 的运动速度为 xcm/s，是否存在实数 x，使得△ACP 与△BPQ 全等？若存在，求出相应的 x、t 的值；若不存在，请说明理由． 【解答】解：（1）△ACP 与△BPQ 全等， 理由如下：当 t＝2 时，AP＝BQ＝4cm， 则 BP＝12﹣4＝8cm， ∴BP＝AC＝8cm， 又∵∠A＝∠B＝90°， 在△ACP 和△BPQ 中， ， ∴△ACP≌△BPQ（SAS）． （2）PC⊥PQ， 证明：∵△ACP≌△BPQ， ∴∠ACP＝∠BPQ， ∴∠APC+∠BPQ＝∠APC+∠ACP＝90°． ∴∠CPQ＝90°， 即线段 PC 与线段 PQ 垂直． （3） ① 若△ACP≌△BPQ， 则 AC＝BP，AP＝BQ， ∴12﹣2t＝8， 解得，t＝2（s）， 则 x＝2（cm/s）． ② 若△ACP≌△BQP， 则 AC＝BQ，AP＝BP， 则 2t＝ ×12， 解得，t＝3（s），则 x＝8÷3＝ （cm/s）， 故当 t＝2s，x＝2cm/s 或 t＝3s，x＝ cm/s 时，△ACP 与△BPQ 全等． 八年级数学期末质量检测试卷（三） 一、选择题（本大题共 10 小题，共 30.0 分） 1. 在直角坐标系中，已知点 rial 在第四象限，则 r A. l 香 䁥 B. l 䁥 C. l ᦙ 䁥 D. l 䁥【答案】A 【解析】解： 点 rial 在第四象限， l 香 䁥 ． 故选：A． 直接利用第四象限内点的坐标特点分析得出答案． 此题主要考查了点的坐标，正确掌握各象限内点的坐标特点是解题关键． i. 下面四幅作品分别代表二十四节气中的“立春”、“芒种”、“白露”、“大雪”， 其中是轴对称图形的是 r A. B. C. D. 【答案】D 【解析】解：A、不是轴对称图形，本选项错误； B、不是轴对称图形，本选项错误； C、不是轴对称图形，本选项错误； D、是轴对称图形，本选项正确． 故选：D． 根据轴对称图形的概念求解即可． 本题考查了轴对称图形的概念 . 轴对称图形的关键是寻找对称轴，图形两部分折叠后可 重合． 3. 已知 y 关于 x 成正比例，且当 i 时， ，则当 1 时，y 的值为 r A. 3 B. 3 C. 12 D. 1i 【答案】B 【解析】解：设 o ， 当 i 时， ， io ，解得 o 3 ， 3 ， 当 1 时， 3 1 3 ． 故选：B． 先利用待定系数法求出 3 ，然后计算 1 对应的函数值． 本题考查了待定系数法求正比例函数的解析式：设正比例函数解析式为 oro 䁥 ， 然后把一个已知点的坐标代入求出 k 即可． 4. 一个三角形的两条边长分别为 3 和 7，则第三边的长可能是 r A. 3 B. 7 C. 10 D. 11 【答案】B 【解析】解：根据三角形的三边关系，得 第三边应 ᦙ 4 ，而 香 1䁥 ． 下列答案中，只有 7 符合． 故选：B． 根据三角形的三边关系“任意两边之和 ᦙ 第三边，任意两边之差 香 第三边”，进行分析 求解． 此题考查了三角形的三边关系． 5. 不等式组 香 1 ᦙi 的解集为 r A. ᦙ i B. 香 1 C. i 香 香 1 D. 无解 【答案】C 【解析】解：不等式组 香 1 ᦙi 的解集为 i 香 香 1 ， 故选：C． 根据“大小小大中间找”可确定不等式组的解集． 本题主要考查不等式的解集，解题的关键是掌握确定不等式组解集的口诀． . 将以点 r 3a䁩 ， r 3a 3 为端点的线段 AB 向右平移 5 个单位得到线段 ， 则线段 的中点坐标是 r A. ria5 B. riai C. r a5 D. r ai 【答案】B 【解析】解： 线段 AB 的中点坐标为 r 3ai ，则线段 的中点坐标是 r 3 5ai 即 riai ， 故选：B． 先求得线段 AB 的中点坐标，再根据横坐标，右移加，左移减；纵坐标，上移加，下移 减求解可得． 本题主要考查坐标与图形的变化 平移，解题的关键是掌握平移变换下点的坐标变化规 律：横坐标，右移加，左移减；纵坐标，上移加，下移减． 䁩. 已知 l 香 䁥 ，则下列不等式中不成立的是 r A. il 香 l B. l i ᦙ 䁥 C. 1 il 香 1 D. l i 香 䁥【答案】C 【解析】解：A、 l 香 䁥 ， il 香 l ，正确，不合题意； B、 l 香 䁥 ， l i ᦙ 䁥 ，正确，不合题意； C、 l 香 䁥 ， 1 il ᦙ 1 ，原式错误，符合题意； D、 l 香 䁥 ， l i 香 䁥 ，正确，不合题意； 故选：C． 直接利用不等式的基本性质分别判断得出答案． 此题主要考查了不等式的性质，正确应用不等式基本性质是解题关键． . 如图， 䁨 中， 䁥 ， ， 䁨 ，将 䁨 折叠，使点 C 与 AB 的中点 D 重合，折痕交 AC 于点 M，交 BC 于点 N，则线段 BN 的长为 r A. 3 B. 4 C. 5 D. 6 【答案】B 【解析】解： 是 AB 中点， ， 3 ， 折叠 ܰ 䁨ܰ ， ܰ 䁨 䁨ܰ ܰ ， 在 ܰ 中， ܰ i ܰ i i ， ܰ i r ܰ i ， ܰ 5 ܰ 4 ， 故选：B． 由折叠的性质可得 ܰ 䁨ܰ ，根据勾股定理可求 DN 的长，即可求 BN 的长． 本题考查了翻折变换，折叠的性质，勾股定理，熟练运用折叠的性质是本题的关键． . 在平面直角坐标系 xOy 中，点 M，N，P，Q 的位置 如图所示 . 若直线 o 经过第一、三象限，则直线 o i 可能经过的点是 r A. 点 M B. 点 N C. 点 P D. 点 Q 【答案】A 【解析】解： 直线 o 经过第一、三象限， 直线 o i 平行直线 o ，且经过 r䁥a i ， 观察图象可知直线 o i 不经过点 N、P、Q， 直线 o i 经过点 M， 故选：A． 根据直线 o i 的位置，利用排除法即可解决问题． 本题考查一次函数图象上的点的坐标特征、一次函数的性质、正比例函数的性质等知识， 解题的关键是灵活运用所学知识解决问题，属于中考常考题型． 1䁥. 如图，在 䁨 中， 䁨 于点 E， 䁨 于点 D；点 F 是 AB 的中点，连结 DF，EF，设 ᦙ ， 䁨 ， 则 r A. B. 1 i 䁥C. i 1䁥D. 䁥 【答案】B 【解析】解： 䁨 于点 E， 䁨 于点 D； 䁥 ， 点 F 是 AB 的中点， ᦙ ᦙ ， ᦙ ᦙ ， ᦙ ᦙ ， ᦙ ᦙ ， ᦙ 1䁥 i䁨 ， ᦙ 1䁥 i䁨 ， 1䁥 ᦙ ᦙ ir䁨 䁨 1䁥 ir1䁥 1䁥 1䁥 i ， 1 i 䁥 ， 故选：B． 由垂直的定义得到 䁥 ，根据直角三角形的性质得到 ᦙ ᦙ ， ᦙ ᦙ ，根据等腰三角形的性质得到 ᦙ ᦙ ， ᦙ ᦙ ，于是得到结论． 本题考查了直角三角形的性质，等腰三角形的性质，三角形的内角和，正确的识别图形 是解题的关键． 二、填空题（本大题共 6 小题，共 18.0 分） 11. 点 ria3 关于 x 轴的对称点的坐标为______． 【答案】 ria 3 【解析】解： 点 ria3 关于 x 轴的对称点的坐标为： ria 3 ． 故答案为： ria 3 ． 根据关于 x 轴对称点的坐标特点：横坐标不变，纵坐标互为相反数 . 即点 ra 关于 x 轴的对称点 的坐标是 ra 得出即可． 此题主要考查了关于 x 轴、y 轴对称点的性质，正确记忆坐标规律是解题关键． 1i. 用不等式表示“a 的 2 倍与 3 的差是非负数”：______． 【答案】 il 3 䁥【解析】解：由题意得： il 3 䁥 ． 故答案为： il 3 䁥 ． 首先表示出a的2倍与3的差为 il 3 ，再表示非负数是： 䁥 ，故可得不等式 il 3 䁥 ． 此题主要考查了由实际问题抽象出一元一次不等式，关键是正确理解题意，要抓住题目 中的关键词“非负数”正确选择不等号． 13. 如图，在 䁨 中，AD 是高，AE 是角平分线，若 䁩i ， 1 ，则 䁨 ______度 . 【答案】40 【解析】解： 是高， 䁩i ， 1 ， 1 1 34 ， 是角平分线， 䁨 ， 䁨 1䁥 䁩i 4䁥 ． 故答案为：40 根据三角形的内角和得出 1 ，再利用角平分线得出 䁨 ，利用三角形 内角和解答即可． 本题考查了三角形的内角和定理，熟悉直角三角形两锐角互余和三角形的内角和等于 1䁥 是解题的关键． 14. 若 r1a1 ， riai 是直线 3 上不同的两点，记 1i 1i ，则函数 i的图象经过第______象限． 【答案】一、三、四 【解析】解： r1a1 ， riai 是直线 3 上不同的两点， 1 31 ， i 3i ， 1i 1i 1i 313i 1 3 ᦙ 䁥 ， 函数 i 的图象经过第一、三、四象限， 故答案为：一、三、四 将点 A，点 B 坐标代入解析式，可得 1 31 ， i 3i ，可得 1 3 ，即可求解． 本题考查了一次函数图象上点的坐标特征，一次函数性质，熟练运用一次函数性质是本 题的关键． 15. 如图，数轴上 A 点表示数 7，B 点表示数 5，C 为 OB 上一点，当以 OC、CB、BA 三条线段为边，可以围成等腰三角形时，C 点表示数______． 【答案】2 或 i.5 或 3 【解析】解： 数轴上 A 点表示数 7，B 点表示数 5， i ， 以 OC、CB、BA 三条线段为边围成等腰三角形时， 若 䁨 i ，则 䁨 5 i 3 ，所以 C 点表示数为 3， 若 䁨 i ，所以 C 点表示数为 2， 若 䁨 䁨 ，则 䁨 5 i i.5 ，所以 C 点表示数为 i.5 ， 故答案为：2 或 i.5 或 3． 根据等腰三角形的两边相等进行解答即可． 本题考查了等腰三角形两边相等的性质，注意分类讨论得出是解题关键． 1. 小婷家与学校之间是一条笔直的公路，小婷从家步行前往学校的途中发现忘记带昨 天的回家作业本，便向路人借了手机打给妈妈，妈妈接到电话后，带上作业本马上 赶往学校，同时小婷沿原路返回 . 两人相遇后，小婷立即赶往学校，妈妈沿原路返 回家，并且小婷到达学校比妈妈到家多用了 5 分钟，若小婷步行的速度始终是每分 钟 100 米，小婷和妈妈之间的距离 y 与小婷打完电话后步行的时间 x 之间的函数关 系如图所示 r1 妈妈从家出发______分钟后与小婷相遇； ri 相遇后妈妈回家的平均速度是每分钟______米，小婷家离学校的距离为______ 米 . 【答案】8 60 2100 【解析】解： r1 当 时， 䁥 ， 故妈妈从家出发 8 分钟后与小婷相遇， ri 当 䁥 时， 14䁥䁥 ， 相遇后 1 1䁥 分钟小婷和妈妈的距离为 1600 米， 1䁥䁥 r1 1䁥䁥 䁥r 米 分 ， 相遇后妈妈回家的平均速度是每分钟 60 米； 1䁥䁥 ri3 1 1䁥䁥 i1䁥䁥r 米 ， 小婷家离学校的距离为 2100 米． 故答案为：8；60；2100． 由当 时， 䁥 ，可得出妈妈从家出发 8 分钟后与小婷相遇； 利用速度 路程 时间结合小婷的速度，可求出小婷和妈妈相遇后，妈妈回家的速度为 60 米 分； 根据路程 1䁥䁥 小婷步行的速度 ri3 1 ，即可得出小婷家离学校的距离． 本题考查一次函数的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利 用数形结合的思想解答． 三、解答题（本大题共 7 小题，共 52.0 分） 1䁩. 解不等式组 ir 3 香 4 i r 1 i 并写出它的整数解． 【答案】解： ir 3 香 4① i r 1 i ② ， 由 ① 得 ᦙ i ， 由 ② 得 ， 故不等式组的整数解为： i 香 ， 它的整数解有 3，4，5，6． 【解析】分别求出各不等式的解集，再求出其公共解集，再其公共解集内找出符合条件 的 x 的整数解即可． 本题考查的是解一元一次不等式组，熟知同大取大；同小取小；大小小大中间找；大大 小小找不到的原则是解答此题的关键． 1. 判断下列命题的真假，若是假命题，请举出反例；若是真命题，请给出证明． ① 若 l ᦙ 㤷 ，则 l i ᦙ 㤷 i ； ② 三个角对应相等的两个三角形全等． 【答案】解： ① 若 l ᦙ 㤷 ，则 l i ᦙ 㤷 i 是假命题， 例如： l 1 ， 㤷 i ， l ᦙ 㤷 ，但 l i 香 㤷 i ； ② 三个角对应相等的两个三角形全等是假命题， 例如：两个边长不相等的等边三角形不全等． 【解析】 ① 根据乘方法则举例即可； ② 根据全等三角形的概念、等边三角形的性质举例． 本题考查的是命题的真假判断，要说明一个命题的正确性，一般需要推理、论证，而判 断一个命题是假命题，只需举出一个反例即可． 1. 如图， 䁨 ， 䁨 ，垂足分别为 D，E，BE 和 CD 相交于点 O， 䁨 ， 连 AO，求证： r1 ≌ 䁨 ； ri 1 i ． 【答案】证明： r1 䁨 ， 䁨 ， 䁨 䁥 ， 在 和 䁨 中， 䁨 䁨 䁨 ， ≌ 䁨r ． ri ≌ 䁨 ， ， ， 䁨 ， 1 i ． 【解析】 r1 根据 AAS 证明 ≌ 䁨 即可； ri 利用角平分线的判定定理证明即可； 本题考查全等三角形的判定和性质，角平分线的判定定理等知识，解题的关键是熟练掌 握基本知识，属于中考常考题型． i䁥. 已知 y 是 x 的一次函数，且当 i 时， 䁩 ；当 3 时， ． r1 求这个一次函数的表达式； ri 求当 i 香 香 4 时 y 的取值范围． 【答案】解： r1 设一次函数解析式为 o 㤷 ， 根据题意得 3o 㤷 io㤷 䁩 ，解得 㤷 1 o 3 ， 所以这个一次函数的表达式为 3 1 ； ri 当 4 时， 3 1 11 ， 所以当 i 香 香 4 时 y 的取值范围为 11 香 香 䁩 ． 【解析】 r1 利用待定系数法求一次函数解析式； ri 先计算出 4 时的函数值，然后根据一次函数的性质求解． 本题考查了待定系数法求一次函数解析式：先设出函数的一般形式，如求一次函数的解 析式时，先设 o 㤷 ；将自变量 x 的值及与它对应的函数值 y 的值代入所设的解析 式，得到关于待定系数的方程或方程组；解方程或方程组，求出待定系数的值，进而写 出函数解析式 . 也考查了一次函数的性质． i1. 格点 䁨 在直角坐标系中的位置如图所示． r1 直接写出点 A，B，C 的坐标和 䁨 的面积； ri 作出 䁨 关于 y 轴对称的 11䁨1 ． 【答案】解： r1 由图知 ria3 ， r3a1 ， 䁨r ia i ， 䁨 的面积为 5 5 1 i 1 i 1 i 3 5 1 i 5 4 13 i ； ri 如图所示， 11䁨1 即为所求． 【解析】 r1 由图可得三顶点的坐标，再根据割补法求解可得； ri 分别作出点 A，B，C 关于 y 轴的对称点，再首尾顺次连接即可得． 此题主要考查了轴对称变换以及三角形面积求法，正确得出对应点位置是解题关键． ii. 如图，在平面直角坐标系 xOy 中，直线 1 ： 3 1与 y 轴交于点 . 直线 i ： 㤷 与直线 1 交于点 r1a ，与 y 轴交于点 C． r1 求 m 的值和点 C 的坐标； ri 已知点 rla䁥 在 x 轴上，过点 M 作直线 3 轴， 分别交直线 1 ， i 于 D，E，若 ，求 a 的值． 【答案】解： r1 把点 r1a 代入 3 1 得， 4 ， 点 C 的坐标为： r䁥a5 ； ri 由 r1 得，直线 i 的解析式为： 5 ， 过点 M 作直线 3 轴，分别交直线 1 ， i 于 D，E， rla3l 1 ， rla l 5 ， ， 3l 1 r l 5 ， l 5 i 或 l 1 i ． 【解析】 r1 把点 r1a 代入 3 1 即可得到结论； ri 由 r1 得到直线 i 的解析式为 4 ，过点 M 作直线 3 轴，分别交直线 1 ， i于 D，E，得到 rla3l 1 ， r l 4 ，列方程即可得到结论． 本题考查了两条直线相交或平行，正确的识别图象是解题的关键． i3. 已知 䁨 是等边三角形，点 D 是 BC 边上一动点，连结 AD r1 如图 1，若 i ， 䁨 4 ，求 AD 的长； ri 如图 2，以 AD 为边作 ᦙ 䁥 ，分别交 AB，AC 于点 E，F． ① 小明通过观察、实验，提出猜想：在点 D 运动的过程中，始终有 ᦙ ，小 明把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的两种想法 想法 1：利用 AD 是 ᦙ 的角平分线，构造角平分线的性质定理的基本图形，然 后通过全等三角形的相关知识获证． 想法 2：利用 AD 是 ᦙ 的角平分线，构造 ᦙ 的全等三角形，然后通过等腰 三角形的相关知识获证． 请你参考上面的想法，帮助小明证明 ᦙ.r 一种方法即可 ② 小聪在小明的基础上继续进行思考，发现：四边形 AEDF 的面积与 AD 长存在很 好的关系 . 若用 S 表示四边形 AEDF 的面积，x 表示 AD 的长，请你直接写出 S 与 x 之间的关系式． 【答案】解： r1 如图，过点 A 作 䁨 于点 G， i ， 䁨 4 ， 䁨 ， 䁨 是等边三角形， 䁨 ， 䁨 ， 1 i 䁨 3 ， 3 i 1 ， 在 中， i i 3 3 ， 在 中， i i i 䁩 ri ① 想法 1：如图，过点 A 作 ᦙ 于点 M，作 ，交 DE 的延长线于点 H， 平分 ᦙ ， ， ᦙ ， ᦙ 䁥 ， ᦙ 1i䁥 ， ᦙ 䁨 ᦙ 3䁥 ， ᦙ 1䁥 ，且 1䁥 ， ᦙ ，且 ， ᦙ 䁥 ， ≌ ᦙr ᦙ想法 2：如图，延长 DE 至 N，使 ܰ ᦙ ， ܰ ᦙ ， ， ᦙ 䁥 ， ܰ≌ ᦙr ܰ ᦙ ， ᦙ ܰ ， ᦙ 䁥 ， ᦙ 1i䁥 ， ᦙ 䁨 ᦙ 3䁥 ， ᦙ 1䁥 ，且 ܰ 1䁥 ， ܰ ᦙ ， ܰ ܰ ， ܰ ᦙ ， ② 如图， 由 ① 中想法 1 可得 ≌ ᦙ ， ᦙ ， 四边形 ᦙ 四边形 ， ᦙ 䁥 ， ᦙ ， 1 i ， 3 3 i ， 1 i 3 i 3 i ， ， ， ≌ rሺ ， 四边形 ᦙ 四边形 i 3 4 i ． 【解析】 r1 由等边三角形的性质可求 䁨 ， 1 i 䁨 3 ， 1 ，由勾股 定理可求 AG，AD 的长； ri ① 想法 1：过点 A 作 ᦙ 于点 M，作 ，交 DE 的延长线于点 H，由角 平分线的性质可得 ，由“AAS”可证 ≌ ᦙ ，可得 ᦙ ； 想法 2：延长 DE 至 N，使 ܰ ᦙ ，由“SAS”可证 ܰ≌ ᦙ ，可得 ܰ ᦙ ， ᦙ ܰ ，由四边形内角和为 3䁥 ，可得 ܰ ᦙ ܰ ，可得 ܰ ᦙ ； ② 由想法 1 可得 四边形 ᦙ 四边形 i 3 4 i ． 本题是三角形综合题，考查了等边三角形的性质，全等三角形的判定和性质，勾股定理 等知识，添加恰当辅助线构造全等三角形是本题的关键．