北师大版数学初中八年级上册课件-第2章-2实数 20页

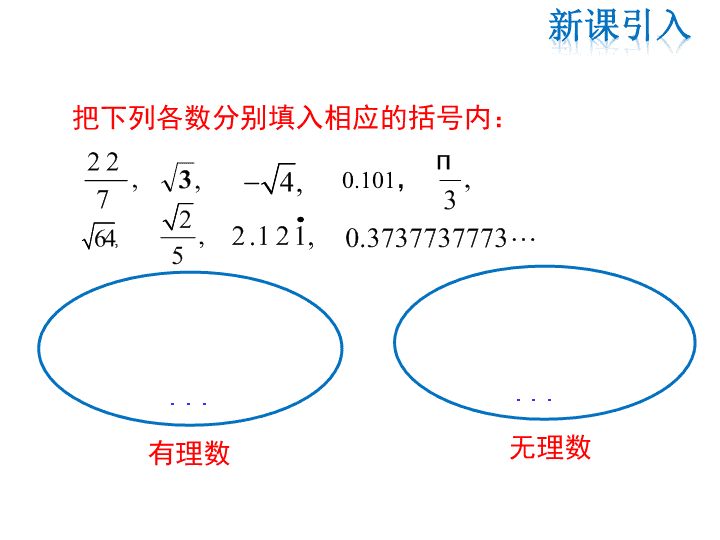
第二章 实数 2.6 实数 学习目标 把下列各数分别填入相应的括号内： 2 2 , 7 2 , 5 4, 0.3737737773   0.101， 2 .1 2 1, ,3 64, 有理数 无理数 ．．． ．．． , 3 π 实数的概念及分类 有理数和无理数统称为实数. 即： 无理数： 无限不循环小 数 有理数： 有限小数或无限循环 小数 实 数 分数 整数 开方开不尽的数 有规律但不循环的数 1 3 2 4 1 7  2 5  2 3 20 5 3 8 9 4 0 7773773373.0 ， ， ， ， ， ， ， ， ， ， ， . , 4 1 , 2 5  ,83 , 9 4 ,23 ,7 , ,2 , 3 20 5 7773773373.0 正数 负数 正实数负实数 数实 负有理数 正有理数 按大小分类： 0 负无理数 正无理数 0 正实数负实数 在实数范围内 ，相反数、倒数、绝对值 的意义和有理数范围内的相反数、倒数、绝 对值的意义完全一样． 例如： 2 与 互为相反数 3 5 与 互为倒数   ||,0|0|,3|3| 2 3 5 1 【问题】在有理数范围内，能进行哪些运算？   3333 2112742724  2552  3 5 153 5 153        判断下列各式成立吗？ 有理数的运算及运算律对实数仍然适用 【例1】分别求下列各数的相反数、倒数和绝对值． .11 (3) ; 225 (2) ; 64 )1( 3  解：(1)∵ ＝－4， ∴ 的相反数是4，倒数是 ，绝对值是4. (2)∵ ＝15， ∴ 的相反数是－15，倒数是 ，绝对值是15. (3) 的相反数是－ ，倒数是 ，绝对值是 . 3 64  3 64  1 4  225 225 1 15 11 11 11 1 11 （1）a是一个实数，它的相反数为 ， 绝对值为 ； （2）如果a ≠0，那么它的倒数为 .  a a 1 a 【练习】 实数与数轴上点的对应关系 【问题1】你能在数轴上找到表示 和 及 这 样的无理数的点吗？ 0 1 2 43-1-2 直径为1的圆 2π 2 π 2 0 1 2 43-1-2 【问题2】边长为1的正方形,对角线长为多少? 22 每一个实数都可以用数轴上的一个点来表示；反 过来，数轴上的每一点都表示一个实数．即实数 和数轴上的点是一一对应的． 【例2】如图所示，数轴上A，B两点表示的数分别 为－1和 ，点B关于点A的对称点为C，求点C所 表示的实数． 解：∵数轴上A，B两点表示的数分别为－1和 ， ∴点B到点A的距离为1＋ ，则点C到点A的距离为 1＋ ， 设点C表示的实数为x，则点A到点C的距离为－1－x， ∴－1－x＝1＋ ， ∴x＝－2－ 3 3 3 3 3 3 本题主要考查了实数与数轴之间的对应关系， 其中利用了：当点C为点B关于点A的对称点时， 点C到点A的距离等于点B到点A的距离；两点之 间的距离为两数差的绝对值． 【例3】如图所示，数轴上A，B两点表示的数分别为 和5.1，则A，B两点之间表示整数的点共有(　　) A．6个 B．5个 C．4个 D．3个 2 解析：∵ ≈1.414，∴ 和5.1之间的整数有2，3， 4，5， ∴A，B两点之间表示整数的点共有4个． 2 2 C 方法总结：数轴上的点与实数一一对应，结合数轴 分析，可轻松得出结论． 1.判断题： ①实数不是有理数就是无理数. （ ） ③无理数都是无限小数. （ ） ④带根号的数都是无理数. （ ） ⑤无理数一定都带根号. （ ） ⑥两个无理数之积不一定是无理数. （ ） ⑦两个无理数之和一定是无理数. （ ） ⑧数轴上的任何一点都可以表示实数.（ ） × × × ②无理数都是无限不循环小数. （ ） √ √ √ √ √ 2.把下列各数填入相应的集合内： 9 3 5 64   6.0 4 3  0 3 9 3 13.0 （1）有理数集合：    （2）无理数集合：    （3）整数集合：             （4）负数集合： （5）分数集合： （6）实数集合： 3 5 π 3 9 3 4  3 9 9 64 3 9 64 0.6  3 4  3 0.13 0.6  3 4  0.13 9 3 5 64 π 0.6  3 4  3 9 3 0.13 3.在 -3，－ ， －1， 0 这四个实数中，最大的 是（ ） A. -3 B.－ C. －1 D. 0 3 3 D 4.如图，在数轴上点A和点B之间的整数是 ． 【解析】1＜ ＜2，2＜ ＜3， 在 与 之间的 整数是2. A B 2 5. 实数 a,b 的位置如图 化简 |a + b| – |a – b| a 0 b 解:由数轴可知，a+b<0，a－b<0，从而 原式=－(a＋b)－[－（a－b）] = －a－b＋（a－b） = －a－b＋（a－b） = －a－b＋a－b = －2b 实数 有理数和无理数统称实数 在实数范围内，相反数、倒数、绝 对值的意义和有理数范围内的相反 数、倒数、绝对值的意义完全一样. 实数与数轴上的点一一对应