八年级数学上册第1章全等三角形1-3探索三角形全等的条件（5）课件（新版）苏科版 14页

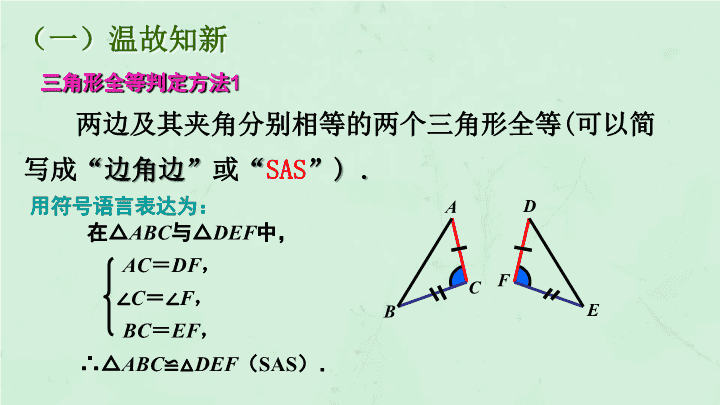
1.3　探索三角形全等的条件SAS,ASA,AAS（5） 如图，已知AB∥CD，线段AD、BC交于点E，要 使△ABE≌ △DCE，请你添加一个条件_________. （一）温故知新 AE=ED 用符号语言表达为： F E D C B A 在△ABC与△DEF中， ∴△ABC≌ △DEF（SAS）． AC＝DF， ∠C＝∠F， BC＝EF， （一）温故知新 F E D C B A 用符号语言表达为： 在△ABC与△DEF中， ∴△ABC≌ △DEF（ASA）． ∠A＝∠D， AB＝DE， ∠B＝∠E， 　　两角分别相等且其中一组等角的对边相等的两个 三角形全等(可以简写成“角角边”或“AAS”）. 用符号语言表达为： 在△ABC与△DEF中， ∴△ABC≌ △DEF（AAS）． ∠A＝∠D， ∠B＝∠E， AC＝DF， 例1：如图,已知AB=AC,AD=AE, ∠BAC=∠DAE. 求证△ABD ≌ △ACE. 二、分析探究 变式1：如图,已知AB=AC,AD=AE, ∠BAC=∠DAE. 求证BD=CE. 变式2：如图,已知△ABC 和△CDE是等边三 角形. 求证∠CBE=∠CAD. 例2：如图，已知，AC⊥CF，EF⊥CF， AB⊥CE，AC=CF. 求证：AB=CE 上面的推理过程可以用符号“”简明地表述如下： 三、了解新知 AC⊥CF, EF⊥CF ∠ACB＝∠F AC=CF AB⊥CE, AC⊥CF ∠ AGC＝∠ACB=90°∠ACG＝∠ABC  △ ACB≌ △ CFE (ASA)  AB＝CE 变式：如图，已知，AC⊥CF，EF⊥CF， ∠A=∠1，AC=CF. 请问AB、CE有怎样的数量和位置关系？ 1 四、归纳总结 根据已有 的判定条 件 寻找隐藏 的判定条 件 证明全等 三角形 对应边和 对应角相 等 转化已有 条件 更多的边、 角关系 更多的边、 角关系 小智同学用数学软件绘制了一张类似“小鱼” 的 几何图形（如下图），已知△ABD≌ △AB’D’. (1)根据△ABD≌ △AB’D’，你 能得到哪些等边、等角？ (2)你能证明△ABC≌ △AB’C’ 吗？那么DC=D’C’吗？ (3)图中还有别的全等三角形吗？ 请你找出并加以证明. 五、拓展练习