- 29.43 KB
- 2021-10-27 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
- 1 -
5.6 几何证明举例
学习目标
1.熟练掌握 AAS,HL 判定定理,等腰三角形,等边三角形性质与判定定理,并会运用这些定
理进行证明相关题目;
2.通过独立思考,合作探究,探究出综合法证明几何问题的方法。
3.全力以赴,达成目标,享受几何证明的多样性之美。
自主探究
(一) 直角三角形全等的判定定理
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对
应相等,那么这两个直角三角形全等。(HL 定理)
【典型例题】
D
F
E
B
C
A
例 1.已知如图,D 是△ABC 的边 BC 的中点,DE⊥AC,DF⊥AB,垂足分别是点 E,F,DE=DF.
求证:△ABC 是等腰三角形.
(二)等腰三角形的性质和判定
命题一:等腰三角形底边上的高、中线及顶角的平分线重合.
已知:
求证:
证明:
命题二:有两个角相等的三角形是等腰三角形.
已知:
求证:
证明:
(三)角平分线与垂直平分线的性质与判定 三角形全等的运用
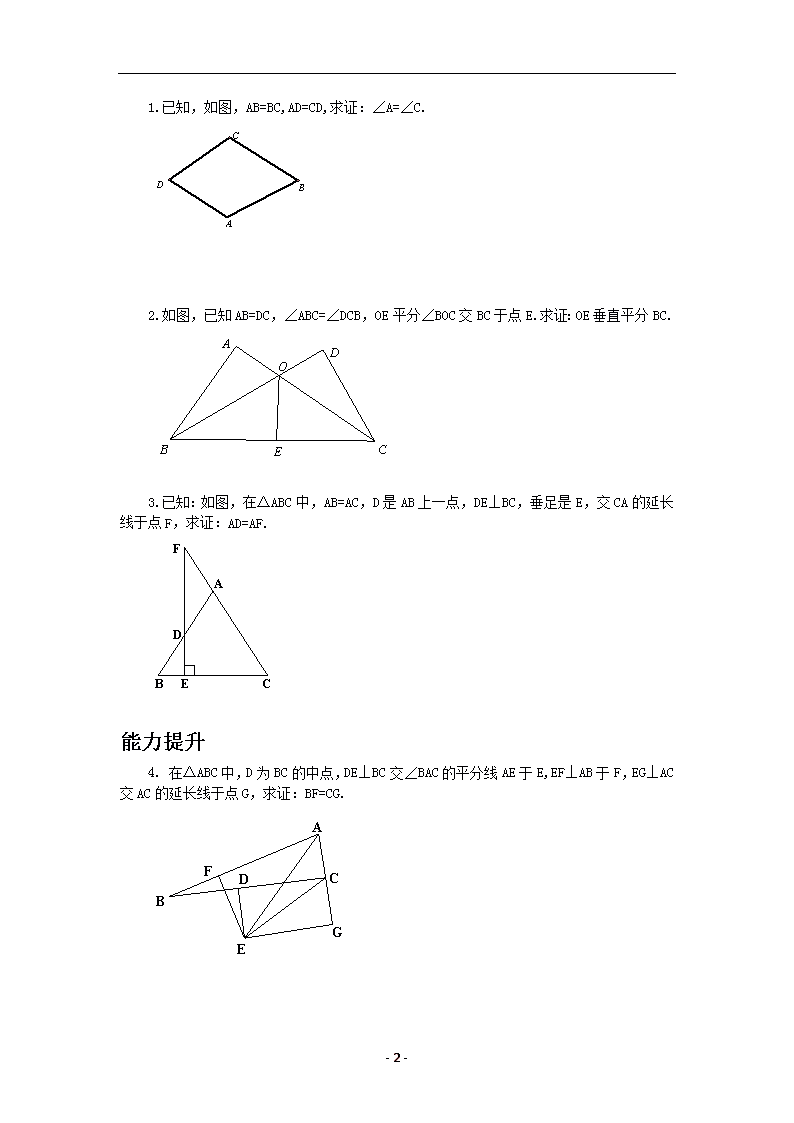
1.已知,如图,AB=BC,AD=CD,求证:∠A=∠C.
- 2 -
C
B
A
D
2.如图,已知 AB=DC,∠ABC=∠DCB,OE 平分∠BOC 交 BC 于点 E.求证:OE 垂直平分 BC.
O
D
C
E
B
A
3.已知:如图,在△ABC 中,AB=AC,D 是 AB 上一点,DE⊥BC,垂足是 E,交 CA 的延长
线于点 F,求证:AD=AF.�
F
�
E
�
D
�
C
�
B
�
A
能力提升
4. 在△ABC 中,D 为 BC 的中点,DE⊥BC 交∠BAC 的平分线 AE 于 E,EF⊥AB 于 F,EG⊥
AC 交 AC 的延长线于点 G,求证:BF=CG.
�
G
�
F
�
E
�
D
�
C
�
B
�
A
相关文档
- 8上北师大版数学第五章二元一次方2021-10-273页
- 八年级数学上册第三章位置与坐标22021-10-275页
- 八年级语文上册第五单元18中国石拱2021-10-2711页
- 2020秋八年级数学上册第一章《勾股2021-10-2715页
- 八年级数学上册第12章整式的乘除122021-10-2718页
- 苏科版八年级上期中数学试卷2021-10-276页
- 八年级下语文课件《变色龙》 (14)_2021-10-2710页
- 广西2018年秋八年级数学上册第3章2021-10-2724页
- 人教版八年级数学上册同步习题课件2021-10-2722页
- 八年级数学下册第六章平行四边形22021-10-2724页