数学华东师大版八年级上册课件13-5 逆命题与逆定理 第2课时 18页

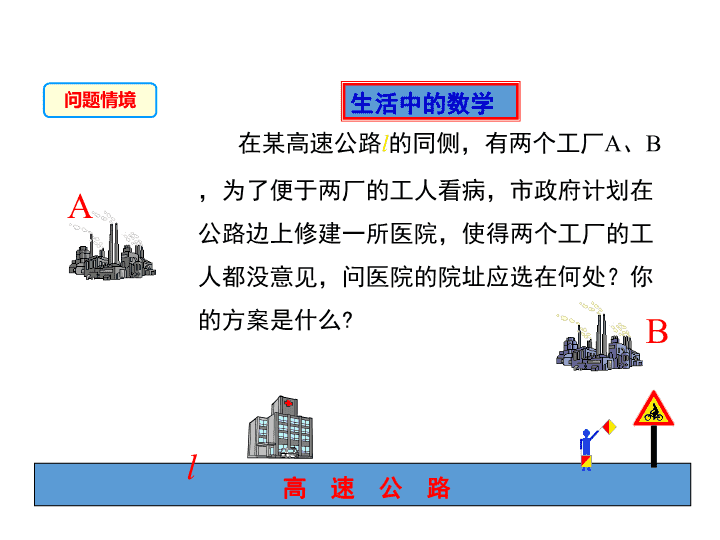
第13章 全等三角形 13.5 逆命题与逆定理 第2课时 1.理解和掌握线段垂直平分线的定理及其逆定理，并能利 用它们来进行证明或计算.(重点) 2.知道线段垂直平分线是到线段两端距离相等的点的集合. 3.了解数学和生活的紧密联系，培养用数学的能力. 学习目标 高 速 公 路 A B 在某高速公路l的同侧，有两个工厂A、B， 为了便于两厂的工人看病，市政府计划在公 路边上修建一所医院，使得两个工厂的工人 都没意见，问医院的院址应选在何处？你的 方案是什么? 生活中的数学 l 问题情境 线段垂直平分线的性质定理一 如图，直线MN是线段AB的垂直平分线，P是MN上 任一点，连结PA、PB.将线段AB沿直线MN对折，你发现 了什么？如何表达，并简述你的证明过程. M N P A C B 对折后PA、PB能够完全重合，PA=PB. 线段是轴对称图形吗？它的对称轴是什么？ 下面我们来证明刚才得到的结论： 证明： ∵MN ⊥AB（已知）, ∴∠ACP=∠BCP=90°(垂直的定义). 在△ACP和△BCP中, ∴ △ACP≌△BCP(S.A.S.). ∴PA=PB(全等三角形的对应边相等). AC=BC, ∠ACP=∠BCP, PC=PC, M N P A C B 你能用一句话来描述刚得到的结论吗？ 线段垂直平分线上的点到线段两端的距离相等. 线段垂直平分线的性质定理： 知识归纳 M N P A C B 几何语言叙述: ∵点P在线段AB的垂直平分线上（或 PC⊥AB，AC=BC）， ∴PA=PB. 这一定理描述了线段垂直平分线的性质，那么反过来 会有什么结果呢？ 写出性质定理及其逆命题的条件和结论，你有什么发现？ t条 件 结 论 性质定理 逆命题 一个点在线段的 垂直平分线上 这个点到线段两 端的距离相等 一个点到线段两 端的距离相等 这个点在线段的 垂直平分线上 想想看，这个逆命题是不是一个真命题？你能证明吗？ 线段垂直平分线的判定定理二 逆命题 如果一个点到线段两端的距离相等，那么 这个点在线段的垂直平分线上. 已知： 如图，QA＝QB. 求证： 点Q在线段AB的垂直平分线上． 分析：为了证明点Q在线段AB的垂直平 分线上，可以先经过点Q作线段AB的垂线， 然后证明该垂线平分线段AB； 也可以先平分线段AB，设线段AB的中 点为点C，然后证明QC垂直于线段AB． 证明：过点Q作MN⊥AB，垂足为点C， 故∠QCA=∠QCB=90°. 在Rt△QCA 和Rt△QCB中， ∵QA=QB，QC=QC， ∴Rt△QCA≌Rt△QCB（H.L.）. ∴AC=BC. ∴点Q在线段AB的垂直平分线上． 已知： 如图，QA＝QB. 求证： 点Q在线段AB的垂直平分线上． 你能根据分析中后一种添加辅助线的方法，写出它的证 明过程吗？ 知识要点 线段垂直平分线的判定 u应用格式： ∵　PA =PB， ∴　点P 在AB 的垂直平分线上． P A B 作用：判断一个点是否在线段的垂直平分线上. 定理 到线段两端距离相等的点在线段的垂直平分线上. 线段垂直平分线的判定定理与性质定理互为逆定理. 利用尺规作三角形三条边的垂直平分线，做完之后， 你发现了什么？ 发现：三角形三边的垂直平分线 交于一点．这一点到三角形三个 顶点的距离相等． 做一做 怎样证明这个结论呢? 点拨：要证明三条直线相交于一点， 只要证明其中两条直线的交点在第三 条直线上即可.思路可表示如下： 试试看，你会写出证明过程吗？ B C A P l n ml是AB的垂 直平分线 m是BC的垂 直平分线   PA=PB PB=PC  PA=PC 点P在AC的垂 直平分线上 证明：连接PA，PB，PC. ∵点P在AB，AC的垂直平分线上， ∴PA=PB，PA=PC （线段垂直平分线上 的点到线段两端距离相等）. ∴PB=PC. ∴点P在BC的垂直平分线上 (到线段两端 距离相等的点在线段的垂直平分线上）. B C A P l n m 当堂练习 1.如图所示，AC=AD,BC=BD,则下列说法正确的是（　　　） A．AB垂直平分CD B ．CD垂直平分AB C．AB与CD互相垂直平分 D．CD平分∠ ACB Ａ Ｂ Ｃ Ｄ 2.已知线段AB，在平面上找到三个点D、E、F，使DA＝DB， EA＝EB,FA＝FB，这样的点在组合共有　　　　种. A 无数 3.下列说法： ①若点P、E是线段AB的垂直平分线上两点，则EA＝EB，PA ＝PB； ②若PA＝PB，EA＝EB，则直线PE垂直平分线段AB； ③若PA＝PB，则点P必是线段AB的垂直平分线上的点； ④若EA＝EB，则经过点E的直线垂直平分线段AB． 其中正确的有 （填序号）.① ② ③ 4.在锐角三角形ABC内一点P,，满足PA=PB=PC,则点P是 △ABC ( ) A.三条角平分线的交点 B.三条中线的交点 C.三条高的交点 D.三边垂直平分线的交点 D 5.如图，△ABC中，AB=AC,AB的垂直平分线交交AC于E, 连接BE，AB+BC=16cm,则△BCE的周长是 cm. A B C D E 16 课堂小结 线段的垂直 平分的性质 和判定 性 质 到线段两端点距离相等的点 在线段的垂直平分线上 内 容 判 定 内 容 作 用 线段垂直平分线上的点到线 段的两个端点的距离相等 作 用 见垂直平分线，得线段相等 判断一个点是否在线段的垂 直平分线上