人教版 八年级下册寒假同步课程（培优版）10函数及图像 8页

1 内容 基本要求 略高要求 较高要求 一次函数 理解正比例函数，能结合具体 情境了解一次函数的意义;会 画一次函数的图像，理解一次 函数的性质 会根据已知条件确定一次函数解析式 ;会根据一次函数解析式求其图像与 坐标轴的交点坐标；能根据一次函数 图像求二元一次方程组的近似解 能用一次函数解决 实际问题 一．一次函数的概念 一般地，形如 y kx b  （ k ，b 是常数， 0k  ）的函数，叫做一次函数，当 0b  时，即 y kx ，这时 即是前一节所学过的正比例函数． （1）一次函数的解析式的形式是 y kx b  ，要判断一个函数是否是一次函数，就是判断是否能化成 以上形式． （2）当 0b  ， 0k  时， y kx 仍是一次函数． （3）当 0b  ， 0k  时，它不是一次函数． （4）正比例函数是一次函数的特例，一次函数包括正比例函数． 二．一次函数的图象 ⑴一次函数 y kx b  （ 0k  ， k ，b 为常数）的图象是一条直线． ⑵由于两点确定一条直线，所以在平面直角坐标系内画一次函数的图象时，只要先描出两个点，再连 成直线即可． ①如果这个函数是正比例函数，通常取  0 0， ， 1 k， 两点； ②如果这个函数是一般的一次函数（ 0b  ），通常取  0 b， ， 0b k     ， ，即直线与两坐标轴的交点． ⑶由函数图象的意义知，满足函数关系式 y kx b  的点  x y， 在其对应的图象上，这个图象就是一条 直线 l ，反之，直线 l 上的点的坐标  x y， 满足 y kx b  ，也就是说，直线 l 与 y kx b  是一一对应的， 所以通常把一次函数 y kx b  的图象叫做直线 l ： y kx b  ，有时直接称为直线 y kx b  ． 三．一次函数的性质 一次 函数  0k kx b k   k ，b 符号 0k  0k  0b  0b  0b  0b  0b  0b  一次函数图象及性质 2 图象 性质 y 随 x 的增大而增大 y 随 x 的增大而减小 1．一次函数图象的位置 在一次函数 y kx b  中： ⑴当 0k  时，其图象一定经过一．三象限；当 0k  时，其图象一定经过二．四象限． ⑵当 0b  时，图象与 y 轴交点在 x 轴上方，所以其图象一定经过一．二象限；当 0b  时，图象与 y 轴 交点在 x 轴下方，所以其图象一定经过三．四象限． 反之，由一次函数 y kx b  的图象的位置也可以确定其系数 k ． b 的符号． 2．一次函数图象的增减性 在一次函数 y kx b  中： ⑴当 0k  时，一次函数 y kx b  的图象从左到右上升， y 随 x 的增大而增大； ⑵当 0k  时，一次函数 y kx b  的图象从左到右下降， y 随 x 的增大而减小． 一．正比例函数的概念 【例 1】 下列函数中，哪些是一次函数？哪些是正比例函数？ （1） 1 5 xy   （2） 5 xy   （3） 2 1y x   （4） 3 5 xy    （5）   2 1 2y x x x    （6） 2 1x y  【例 2】 已知 3ay ax  ，若 y 是 x 的正比例函数，则 a 的值是 ． 【例 3】 已知 y m 与 x n （m,n 为常数）成比例，试判断 y 与 x 成什么函数关系？ 【巩固】已知 2y  与 x 成正比例，当 3x  时， 1y  ,求 y 与 x 之间的函数关系式，并判断它是不是正比例 函数． 3 【例 4】 函数已知 2 8( 3) 1my m x    ，当 m 为何值时，y 是 x 的一次函数？ 【巩固】已知 2( 1) 1y m x m    ，当 m 取何值时，y 是 x 的正比例函数？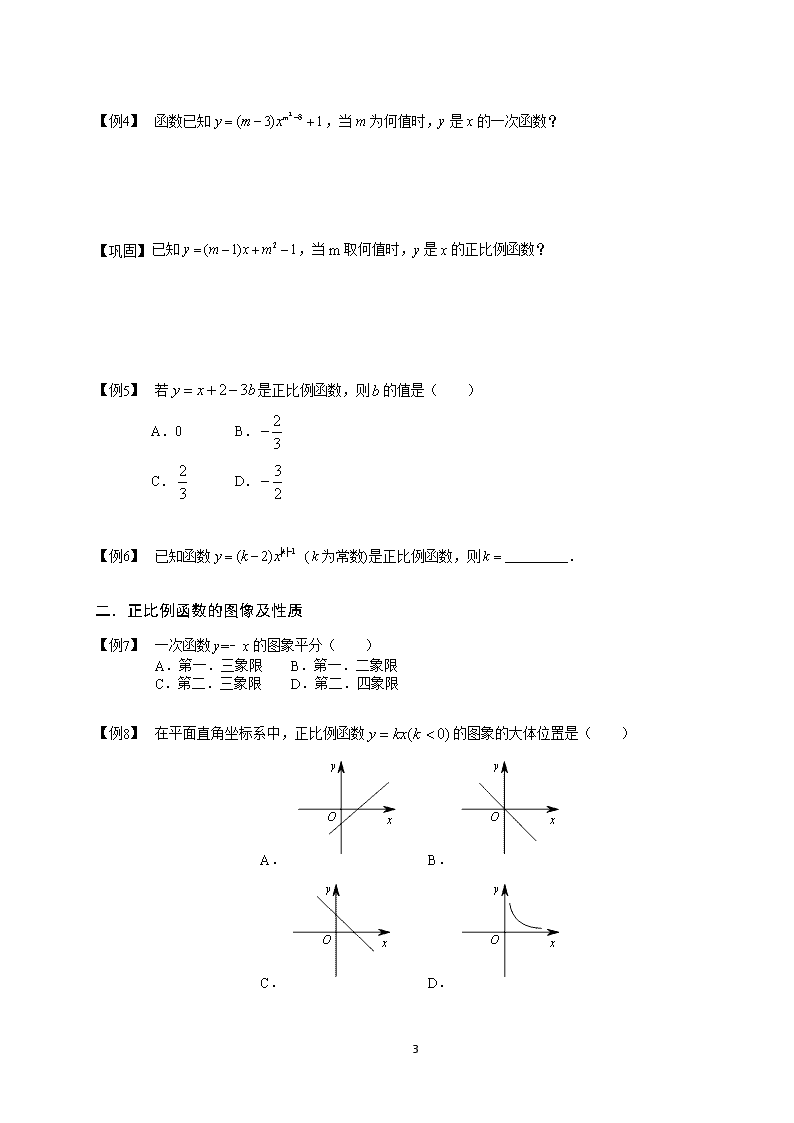 【例 5】 若 2 3y x b   是正比例函数，则b 的值是（ ） A．0 B． 2 3  C． 2 3 D． 3 2  【例 6】 已知函数 1( 2) ky k x   ( k 为常数)是正比例函数，则 k  ． 二．正比例函数的图像及性质 【例 7】 一次函数 y=﹣x 的图象平分（ ） A．第一．三象限 B．第一．二象限 C．第二．三象限 D．第二．四象限 【例 8】 在平面直角坐标系中，正比例函数 ( 0)y kx k  的图象的大体位置是（ ） A． B． C． D． 4 【例 9】 下列表示一次函数 y mx n  与正比例函数 y mnx (m n、 为常数， 0mn 且 ）图象中，一定 不正确的是（ ） A． B． C． D． 【例 10】已知正比例函数 y kx ( 0k  ， k 为常数)，经过点(2，4)，以下哪个点不在该正比例函数图图象 上( ) A．(-2，-4) B．(0，0) C．(1，2) D．(1， 2y x ) 三．一次函数的概念及性质 【例 11】在坐标系中画出下列函数的图象. ⑴ 2y x ； 2 3y x  ； 2 1y x  ；⑵ 1 2y x  ； 1 22y x   ； 1 22y x   【巩固】如图所示，在同一直角坐标系中，一次函数 1y k x ， 2y k x ， 3y k x ， 4y k x 的图像分别是 1l ， 2l ， 3l ， 4l ；那么 1k ， 2k ， 3k ， 4k 的大小关系是 ． 5 【例 12】若一次函数 2 2 22 2m my x m    的图象经过第一．第二．三象限，求 m 的值． 【例 13】若一次函数 2(1 ) 12 ky k    的图象不经过第一象限，则 k 的取值范围是 ． 【例 14】如果一次函数 y kx b  的图象经过第一象限，且与 y 轴负半轴相交，那么（ ） A. 0 0k b ， B. 0 0k b ， C. 0 0k b ， D. 0 0k b ， 【例 15】已知点   1 24 2y y ， ， ， 都在直线 1 22y x   上，则 1 2y y， 大小关系是（ ） A． 1 2y y B. 1 2y y C． 1 2y y D．不能比较 【例 16】一次函数的图象过点  1,0 ，且函数值随着自变量的增大而减小，写出一个符合这个条件的一次 函数解析式 ． 【巩固】已知一次函数的图象过点  0,3 与  2,1 ，则这个一次函数 y 随 x 的增大而 ． 【例 17】 已知一次函数 y kx k  ，若 y 随 x 的减小而减小，则该函数的图象经过（ ） A．第一．二．三象限 B．第一．二．四象限 C．第一．三．四象限 D．第二．三．四象限 6 【巩固】若 0ab  ， 0bc  ，则 a ay xb c    经过（ ） A．第一．二．三象限 B．第一．三．四象限 C．第一．二．四象限 D．第二．三．四象限 【例 18】⑴将直线 2y x 向右平移 2 个单位所得的直线的解析式是 . ⑵直线 2 2y x  向右平移 3 个单位，再向下平移 2 个单位，所得到的直线的解析式是 . 【例 19】如果直线 y ax b  不经过第四象限，那么 ab 0 （填“≥ ”．“≤ ”．“  ”）． 【例 20】下面哪个正比例函数的图象经过一．三象限 ( ) A．  2 3y x  B．  3.14 πy x  C. π2 2y x     D．  5 2 6y x  【例 21】已知一次函数 (5 ) 1y a x a    的图象如图所示，则 a 的取值范围是 . 【例 22】已知一次函数 (3 ) ( 2)y k x k    ( k 为常数)的图象经过一．二．三象限，求 k 取值范围． 【例 23】如图的坐标平面上有四直线 L1．L2．L3．L4．若这四直线中，有一直线为方程式3 5 15 0x y   的图形，则此直线为何？（ ） 7 A．L1 B．L2 C．L3 D．L4 课后作业 【习题 1】正比例函数 y=kx 的图象是经过原点的一条（ ） A．射线 B．双曲线 C．线段 D．直线 【习题 2】函数   22 11 my m x mn   在 ______ 条件下， y 是 x 的一次函数；在_________条件下， y 与 x 成正比例函数． 【习题 3】已知 1( 2) 2my m x m    是一次函数，求它的解析式． 【习题 4】（1）如果一次函数 y kx b  的图象经过第一象限，且与 y 轴负半轴相交，那么( ) A． 0k  ， 0b  B． 0k  ， 0b  C． 0k  ， 0b  D． 0k  ， 0b  （2）已知一次函数 y kx b  的图象经过( 1x ， 1y )和( 2x ， 2y )两点，且 1 2x x , 1 2y y ，则( ) A． 0k  B． 0k  ， 0b  C． 0k  ， 0b  D． 0k  （3）已知一次函数 y kx k  ，若 y 随 x 的减小而减小，则该函数的图象经过( ) A．第一．二．三象限 B．第一．二．四象限 C．第一．三．四象限 D．第二．三．四象限 （4）如图，一次函数 1y ax a   的图象大致是( ) 8 A B C D （5）若 0ab  ， 0bc  ，则 a ay xb c    经过( ) A．第一．二．三象限 B．第一．三．四象限 C． 第一．二．四象限 D．第二．三．四象限 【习题 5】函数 y ax b  ①和 y bx a  ②（ 0ab  )在同一坐标系中的图像可能是( ) 【习题 6】当 k 的取值范围为_______时，关于 x 的方程 2 2 5 2x k x x      至少有 3个解． A. 3k  B. 3 7k  C. 3 7k  D. 3 7k 