八年级数学上册第四章一次函数小结与复习教学课件新版北师大版 21页

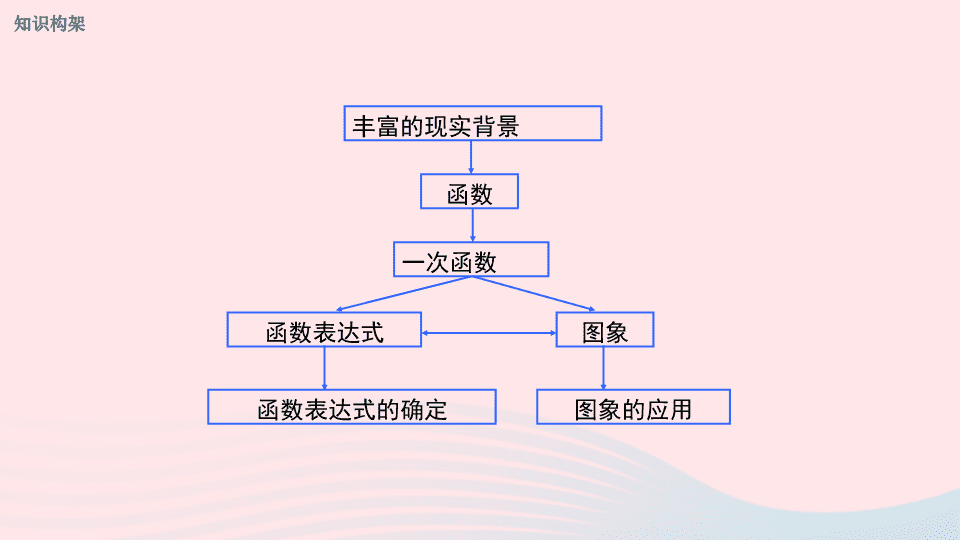
小结 与 复习 第四章 一次函数 丰富的现实背景 函数 一次函数 函数表达式 图象 函数表达式的确定 图象的应用 知识构架 函数 一 1. 叫变量， 叫常量 . 2. 函数定义： 数值发生变化的量 数值始终不变的量 在一个变化过程中，如果有两个变量 x 与 y ，并且对于 x 的每一个确定的值， y 都有 唯一 确定的值与其对应，那么我们就说 x 是自变量， y 是 x 的函数 . 知识梳理 ( 所用方法 : 描点法 ) 3. 函数的图象： 对于一个函数，如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象 . 列表法 解析式法 图象法 5. 函数的三种表示方法： 4. 描点法画图象的步骤： 列表、描点、连线 一次函数与正比例函数的概念 二 一次函数 一般地，如果 y ＝ k x ＋ b ( k 、 b 是常数， k ≠0) ，那么 y 叫做 x 的一次函数 正比例函数 特别地，当 b ＝ ____ 时，一次函数 y ＝ k x ＋ b 变为 y ＝ ___ ( k 为常数， k ≠0) ，这时 y 叫做 x 的正比例函数 注意： 一次函数与正比例函数的关系 0 kx 一次函数的图象与性质 三 函数 字母取值 （ k >0 ） 图象 经过的象限 函数性质 y ＝ kx + b ( k ≠0) b >0 y 随 x 增大而 增大 b =0 b <0 一、三象限 一、二、三象限 一、三、四象限 函数 字母取值 （ k<0 ） 图象 经过的象限 函数性质 y ＝ kx+b ( k≠0 ) b>0 ________ y 随 x 增大而 减小 b ＝ 0 ________ b <0 ________ 一、二、四象限 二、四象限 二、三、四象限 求一次函数的表达式 四 求一次函数表达式一般步骤： （ 1 ）先设出函数表达 式 ； （ 2 ）根据条件列关于待定系数的方程（组）； （ 3 ）解方程（组）求出表达 式中未知的系数 ； （ 4 ）把求出的系数代入设的表达式，从而具体写出这个表达式 . 1. 　填空题： 　　有下列函数：①　　　　　 , ② 　　　　 , ③ 　　　 , ④ . 其中过原点的直 线是 _____ ；函数 y 随 x 的增大而增大的是 ___________ ；函数 y 随 x 的增大而减小的是 ______ ；图象在第一、二、三象限的是 _____. ② ①、②、③ ④ ③ x y 2 = 当堂练习 k ___0 ， b ___0 k ___0 ， b___ 0 k ___0 ， b ___0 k ___0 ， b ___0 2. 根据下列一次函数 y = kx + b ( k ≠ 0) 的 草图回答出各图中 k 、 b 的 符号： < > < > > > < < 3 、在下列函数中， x 是自变量， y 是 x 的函数， 哪些是一次函数？哪些是正比例函数？ y =2 x y =-3 x +1 y = x 2 4 、某函数具有下列两条性质 （ 1 ）它的图像是经过原点（ 0 ， 0 ）的一条直线； （ 2 ） y 的值随 x 值的增大而增大 . 请你举出一个满足上述条件的函数（用关系式表示） . y =3 x 解： (1)(2) 是一次函数，其中 (1) 是正比例函数 . 5. 函数 的图象与 x 轴交点的坐标为 ______, 与 y 轴的交点坐标为 ______. (-6,0) (0,4) 6. 已知函数 y =- x +2. 当 -1< x ≤1 时 , y 的取值范围是 _______. 1≤ y <3 7. 已知一次函数 y = kx+b , y 随着 x 的增大而减小 , 且 kb <0, 则在直角坐标系内它的大致图象是 ( 　 ) A 　　　　　 B 　 C 　 　 D A 　 8. 一次函数 y=ax+b 与 y=ax+c ( a >0) 在同一坐标系中的图象可能是（　 　） x y o x y o x y o x y o A B C D A 9. 小星以 2 米 / 秒的速度起跑后，先匀速跑 5 秒，然后突然把速度提高 4 米 / 秒，又匀速跑 5 秒 . 试写出这段时间里他的跑步路程 s （单位：米）随跑步时间 x （单位：秒）变化的函数关系式，并画出函数图象 . 解 : 依题意得 { s =2 x (0≤ x ≤5) s =10+6( x -5) (5< x ≤10) 10 0 s( 米 ) 5 0 x( 秒 ) ① 40 10 s( 米 ) 10 5 x( 秒 ) ② x( 秒） s( 米 ) o · · · · 5 10 10 40 · · · s=2x (0≤x≤5) s=10+6(x-5) (5