人教版 八年级下册寒假同步课程（培优版）7特殊的平行四边形 8页

1 知识点 A要求 B要求 Ｃ要求 矩形 会识别矩形 掌握矩形的概念A、判定和性质，会用矩形的性质及 判定解决简单问题 会运用矩形的知识解决有关 问题 模块一 矩形的性质及判定 1．矩形的定义：有一个角是直角的平行四边形叫做矩形． 2．矩形的性质 矩形是特殊的平行四边形，它具有平行四边形的所有性质，还具有自己独特的性质： ① 边的性质：对边平行且相等． ② 角的性质：四个角都是直角． ③ 对角线性质：对角线互相平分且相等． ④ 对称性：矩形是中心对称图形，也是轴对称图形． 直角三角形斜边上的中线等于斜边的一半． 直角三角形中， 30 角所对的边等于斜边的一半． 点评：这两条直角三角形的性质在教材上是应用矩形的对角线推得，用三角形知识也可推得． 3．矩形的判定 判定①：有一个角是直角的平行四边形是矩形． 判定②：对角线相等的平行四边形是矩形． 判定③：有三个角是直角的四边形是矩形． 【例 1】 矩形具有而平行四边形不具有的性质为（ ） A．对角线相等 B．对角相等 C．对角线互相平分 D．对边相等 【例 2】 如图，矩形 ABCD 沿 AE 折叠，使 D 点落在 BC 边上的 F 点处，如果 60BAF   ， 则 DAE  【巩固】矩形 ABCD 中，点 H 为 AD 的中点，P 为 BC 上任意一点，PE HC 交 HC 于点 E ，PF BH 交 BH 于点 F ，当 AB BC， 满足条件 时，四边形 PEHF 是矩形 【例 3】 如图，在四边形 ABCD 中， 90ABC BCD     ， AC BD ，求证：四边形 ABCD 是矩形． 特殊的平行四边形 2 C D B A 【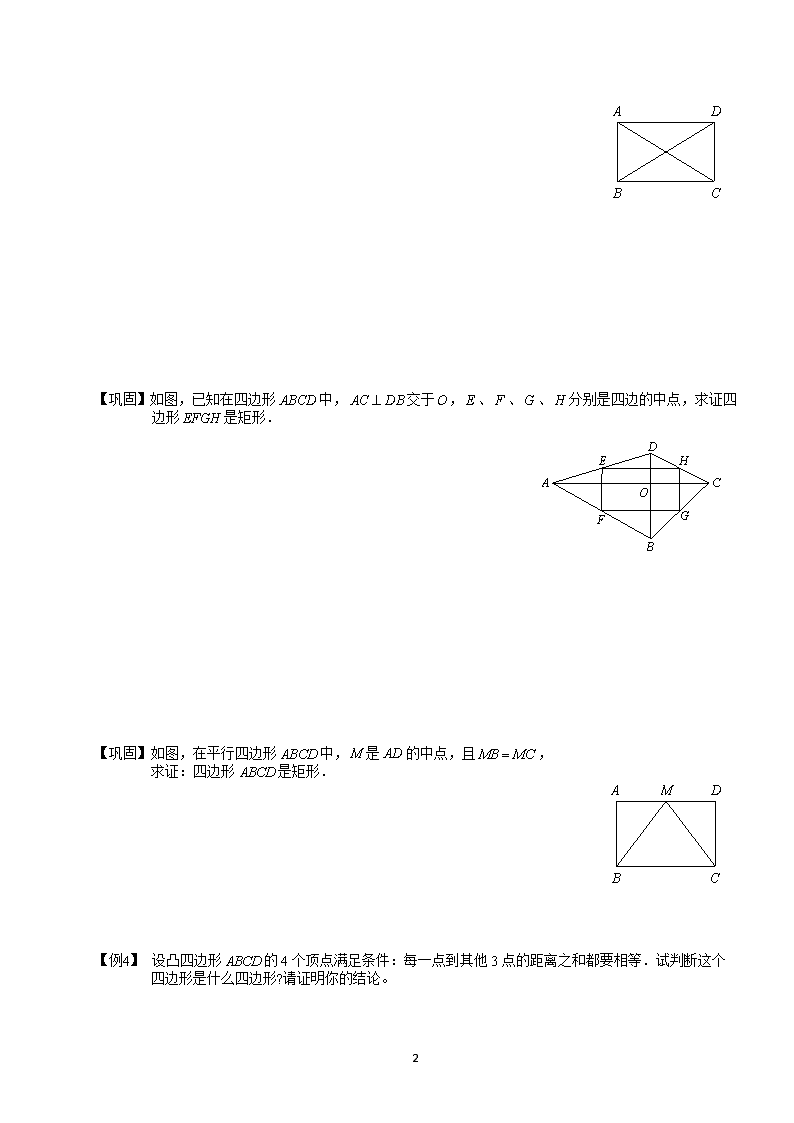巩固】如图，已知在四边形 ABCD 中， AC DB 交于O ， E 、 F 、 G 、 H 分别是四边的中点，求证四 边形 EFGH 是矩形． H G O F E D C B A 【巩固】如图，在平行四边形 ABCD 中， M 是 AD 的中点，且 MB MC ， 求证：四边形 ABCD 是矩形． M C D B A 【例 4】 设凸四边形 ABCD 的 4 个顶点满足条件：每一点到其他 3 点的距离之和都要相等．试判断这个 四边形是什么四边形?请证明你的结论。 3 【例 5】 已知矩形 ABCD 和点 P ，当点 P 在矩形 ABCD 内时，试求证： PBC PAC PCDS S S △ △ △ P A B C D 【例 6】 （西城区抽样测试）如图，将矩形 ABCD 沿 AC 翻折，使点 B 落在点 E 处，连接 DE 、 CE ，过 点 E 作 EH AC ，垂足为 H ． ⑴判断 ACED 是什么图形,并加以证明； ⑵若 8AB  ， 6AD  ．求 DE 的长； ⑶四边形 ACED 中，比较 AE EC 与 AC EH 的大小． D C B A E H 【例 7】 如图所示，在矩形 ABCD 和矩形 BFDE 中，若 AB BF ，求证： MN CF ． 4 N M F E D C B A 【例 8】 已知，如图，矩形 ABCD 中， CE BD 于 E ， AF 平分 BAD 交 EC 于 F ，求证： CF BD ． D A B C E F 【例 9】 如图，在 ABC 中，D 是 BC 边上的一点，E 是 AD 的中点，过 A 点作 BC 的平行线交 CE 的延长 线于点 F ，且 AF BD ，连结 BF ． ⑴ 求证： BD CD ． ⑵ 如果 AB AC ，试判断四边形 AFBD 的形状，并证明你的结论． F E D C B A 5 【巩固】如图，在 ABC 中，点 D 是 AC 边上的一个动点，过点 D 作直线 MN BC∥ ，若 MN 交 BCA 的 平分线于点 E ，交 BCA 的外角平分线于点 F （1）求证： DE DF （2）当点 D 运动到何处时，四边形 AECF 为矩形？请说明理由！ 【例 10】 如图，在矩形 ABCD 中， ,E F 分别是 ,BC AD 上的点，且 BE DF . 求证： ABE ≌ CDF . D E F C A B 【例 11】 如图，在矩形 ABCD 中，点 E 是 BC 上一点， AE AD ， DF AE ，垂足为 F .线段 DF 与 图中的哪一条线段相等？先将你猜想出的结论填写在下面的横线上，然后再加以证明。即 DF  .(写出一条线段即可) 6 E F D C A B 【例 12】 如图，平行四边形 ABCD 中，AQ 、BN 、CN 、DQ 分别是 DAB 、 ABC 、 BCD 、 CDA 的平分线， AQ 与 BN 交于 P ，CN 与 DQ 交于 M ，证明：四边形 PQMN 是矩形． N M Q P D C B A 【巩固】如图，四边形 ABCD 是矩形，∠EDC=∠CAB，∠DEC=90°． （1）求证：AC∥DE； （2）过点 B 作 BF⊥AC 于点 F，连接 EF，试判别四边形 BCEF 的形状，并说明理由． 【巩固】如图，点 E 是矩形 ABCD 的对角线 BD 上的一点，且 BE=BC，AB=3，BC=4，点 P 为直线 EC 上的一点，且 PQ⊥BC 于点 Q，PR⊥BD 于点 R． 7 （1）如图 1，当点 P 为线段 EC 中点时，易证：PR+PQ= 12 5 （不需证明）． （2）如图 2，当点 P 为线段 EC 上的任意一点（不与点 E、点 C 重合）时，其它条件不变，则（1） 中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由． （3）如图 3，当点 P 为线段 EC 延长线上的任意一点时，其它条件不变，则 PR 与 PQ 之间又具有 怎样的数量关系？请直接写出你的猜想 模块二 斜边中线的性质 【例 13】 如图，矩形 ABCD 的两条对角线相交于点O ， 60AOB   ， 2AB  ，则矩形的对角线 AC 的 长是（ ） A． 2 B． 4 C． 2 3 D． 4 3 O D C B A 【例 14】 矩形 ABCD 的对角线 AC 、BD 交于O ，如果 ABC 的周长比 AOB 的周长大10cm ，则边 AD 的长是 ． 【例 15】 如图，矩形 ABCD 中，对角线 AC BD， 相交于点 O ， AE BO 于 E ， OF AD 于 F ，已知 8 3cmOF  ，且 : 1:3BE ED  ，求 BD 的长． 课后作业 1. 已知，如图，在 ABC 中， AB AC ， AD 是 BC 边上的高， AF 是 BAC 的外角平分线， DE ∥ AB 交 AF 于 E ，试说明四边形 ADCE 是矩形． 3 2 1 F E D C B A 2. 如图所示，在 Rt ABC 中， 90ABC   ，将 Rt ABC 绕点C 顺时针方向旋转 60 得到 DEC 点 E 在 AC 上，再将 Rt ABC 沿着 AB 所在直线翻转180 得到 ABF 连接 AD ． ⑴ 求证：四边形 AFCD 是菱形； ⑵ 连接 BE 并延长交 AD 于G 连接 CG ，请问：四边形 ABCG 是什么特殊平行四边形？为什么？ A B C D G E F