- 1.72 MB
- 2021-11-01 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
中小学精品教学资源
中小学精品教学资源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中小学精品教学资源
中
小
学
精
品
教
学
资
源
中小学精品 学资源
中小学精品教学
源
中
小
学
精
品
教
学
资
源
中小学精品教学资源
中
小
学
精
品
教
学
资
源
中小学精品教学资源
中小学精品教学资源中小学精品教学资源
中小学精品教学资源
中 学精品教学资源
中
小
学
精
品
教
学
资
源
中小学精品教学资源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中小学精品教学资源
中小学精品教学资源
中小 精品教学资源
中小学精品教学资源
中小学精品教学资源
中小学精品教学资源中
精品教学资源
中小
精品教学资源
中小学精品教学资源
中小学精品教学资源
中小学精品教学资源
中小学精品教学资源
中小学精品教学资源
中小学精品教学资源
中小学精品教学资源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中小学精品
学资源
中
小
学
精
品
教
学
资
源
中小学精品教学资源
中小学精品教学资源中小学精品教学资源
中小学精品教学资源
中 学精品教学资源
中
精品教学资源
中小学精品教学资源
中小
品教学
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
资
源
中
小
精
品
教
学
资
源
中小学精品教
资源
中
小
学
精
品
教
学
资
源中小学精品教
资源
中
小
学
精
教
学
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
资
源
中
小
学
精
品
学
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中小学精品教学资源
中小学精 教学资中小学精品教学资
中小学精品教学资源
中小学精品教学资源
中小
精品教学资源
中小学
品教学资源
中小
精品教学资源
中小 精品教 资源
中小学精品教学资源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中小学精品教学 源
中
小
学
精
品
教
学
资
源
中小学精品
资源
中小学精品教学
源
中
小
学
精
品
教
学
资
源
中小学精品教学资源
中
小
学
精
品
教
学
资
源
小学精品教
资源
中小学精品教 资源中小学精品教学资源
学精品教学资源
中 学精 教学资源
中
小
学
精
品
教
学
资
源
中 学资源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中小学精品教学资源
中小学精品教学资源
中小 精品教学资源
中小学精品教学资源
中小学精品教学资源
中小学 品教学资源中
精品教学资源
小
精品教学资源
中小学精品教学资源
中小学精品教学资源
中
学精品教学资
中小
精品教学资源
中小学精品教学资源
中小学精品
中小 精品教 资源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中小
精品
学资源
中
小
学
精
品
教
学
资
源
中小
精品
学资源
中 学精品教 资源中小
精品教学资源
中小学精品教学资源
中 学精品 资源
中
教学资源
中
精
教学资源
中小
品教学
源
中
小
学
精
品
教
学
资
源
小
学
精
品
教
学
资
源
中
小
学
品
教
资
源
中
小
学
品
教
资
源
中
小
品
教
资
源小学精品教
资
中
小
学
精
品
教
学
资
源中小学精品教
资
中
小
学
精
教
学
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
资
源
中
小
学
精
品
教
学
资
中
小
学
精
品
教
学
资
源
中
小
学
精
品
教
学
资
源
中
学
精
品
教
资
源
中
小
学
品
学
资
源
中
小
学
精
品
教
学
资
源
中
小
精
品
教
学
资
源
中小学精品教学资源
中小 精 教中小学精品教学
中小学精品教学资源
中小学 品教学资
中小
精品教学资源
中小
品教学资源
精品教学资源
第十八章 平行四边形
18.1 平行四边形
第4课时 平行四边形的判定(二)
课前预习
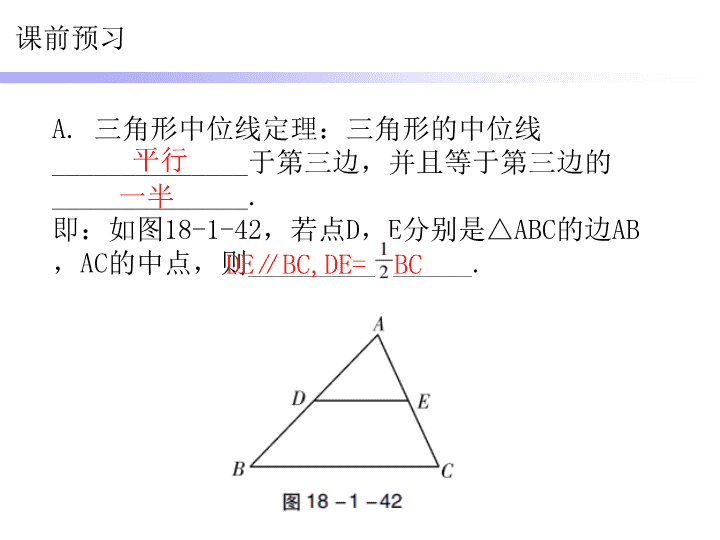
A. 三角形中位线定理:三角形的中位线
______________于第三边,并且等于第三边的
______________.
即:如图18-1-42,若点D,E分别是△ABC的边AB,
AC的中点,则________________.
平行
一半
DE∥BC,DE= BC
1.如图18-1-43,在□ABCD中,AD=8,点E,F分别是BD,
CD的中点,则EF=__________. 4
2. 如图18-1-44,在□ABCD中,AC,BD相交于点O,E
是AB的中点,∠BEO=120°,则∠BAD=__________.
3. 如图18-1-45,D,E,F分别为△ABC三边的中点,
则图中平行四边形有__________个.
120°
3
课堂讲练
【例】如图18-1-46,等边三角形ABC的边长是2,D,E
分别为AB,AC的中点,延长BC至点F,使CF= BC,连
接CD和EF.
(1)求证:DE=CF;(2)求EF的长.
知识点 三角形中位线定理
(1)证明:∵D,E分别为AB,AC的中点,
∴DE∥BC且DE= BC.
∵CF= BC,
∴DE=CF.
(2)解:由(1)得DE∥FC,DE=FC,
∴四边形DEFC是平行四边形.∴DC=EF.
∵D为AB的中点,等边三角形ABC的边长是2,
∴AD=BD=1,CD⊥AB,BC=2.
∴EF=DC= = .
1. 如图18-1-47,在△ABC中,M是BC的中点,
AN平分∠BAC,AN⊥BN于N,延长BN交AC于点D,
已知AB=10,MN=4,BM=7,求△ABC的周长.
解:在△ANB和△AND中,
∠BAN=∠DAN,
AN=AN,
∠ANB=∠AND=90°,
∴△ANB≌△AND(ASA).
∴AD=AB=10,BN=BD.
∵M是BC的中点,BN=BD,
∴BC=2BM=14,CD=2MN=8,
∴△ABC的周长=AB+BC+AC=10+14+8+10=42.
分层训练
【A组】
1. 如图18-1-48,在四边形ABCD中,对
角线AC,BD相交于点E,∠CBD=90°,BC
=4,BE=ED=3,AC=10,则四边形ABCD
的面积为( )
A. 6 B. 12
C. 20 D. 24
D
2. 如图18-1-49,在四边形ABCD中,P是对角线BD
的中点,E,F分别是AB,CD的中点,AD=BC,
∠PEF=30°,则∠EPF的度数是( )
A. 120° B. 150°
C. 135° D. 140°
A
3. 如图18-1-50,AB是池塘两端,设计一方法测量
AB的距离,取点C,连接AC,BC,再取它们的中点D,
E,测得DE=15 m,则AB=( )
A.7.5 m
B.15 m
C.22.5 m
D.30 m
D
4. 如图18-1-51,在Rt△ABC中,∠C=90°,
AB=10,AC=6,D,E,F分别是△ABC三边的中点,
则△DEF的周长为( )
A. 24 B. 16
C. 14 D. 12
D
5. 如图18-1-52,在△ABC中,D,E分别是AB和AC的中
点,F是BC延长线上一点,CF=1,连接DF交CE于点G,且
EG=CG,则BC=__________.
6. 如图18-1-53,CD是△ABC的中线,点E,F分别是AC,
DC的中点,EF=1,则BD=__________.
2
2
7. 如图18-1-54,在△ABC中,M,N分别是AB,
AC的中点,且∠A+∠B=136°,则
∠ANM=__________.
44°
8. 如图18-1-55,DE为△ABC的中位线,点F为
DE上一点,且∠AFB=90°,若AB=6,BC=8,
求EF的长.
解:∵DE为△ABC的中位
线,
∴DE= BC=4,
∵∠AFB=90°,D是AB的
中点,
∴DF= AB=3,
∴EF=DE-DF=1.
9. 如图18-1-56,AD,AE分别是△ABC的角平分
线和中线,CG⊥AD于点F,交AB于点G,若AB=8,
AC=6,求EF的长.
【B组】
解:∵AD为△ABC的角平分线,CG⊥AD,
∴△ACG是等腰三角形.
∴AG=AC.
∵AC=6,
∴AG=AC=6,FG=CF.
∵AE为△ABC的中线,
∴EF是△BCG的中位线.
∴EF= BG.
∵AB=8,
∴BG=AB-AG=8-6=2.
∴EF=1.
10. 如图18-1-57,在△ABC中,AB=AC,CD是AB边上
的中线,延长AB到点E,使BE=AB,连接CE.求证:
CD= CE.
证明:如答图18-1-5,作BF∥AC交EC于点F.
∵BF∥AC,∴∠FBC=∠ACB.
∵AB=AC,∴∠ABC=∠ACB.
∴∠FBC=∠ABC.
∵BF∥AC,BE=AB,∴BF= AC,CF= CE.
∵CD是AB边上的中线,
∴BD= AB.
∴BF=BD.
在△FBC和△DBC中,
∵BF=BD,∠FBC=∠DBC,BC=BC,
∴△FBC≌△DBC.
∴CD=CF.
∴CD= CE.
11. 如图18-1-58,点O是△ABC内一点,连接
OB,OC,线段AB,OB,OC,AC的中点分别为D,
E,F,G.
(1)判断四边形DEFG的形状,并说明理由;
(2)若M为EF的中点,OM=2,∠OBC和∠OCB
互余,求线段BC的长.
解:(1)四边形DEFG是平行四边形,
理由如下:∵E,F分别为线段OB,OC的中点,
∴EF= BC,EF∥BC.
同理DG= BC,DG∥BC.
∴EF=DG,EF∥DG.
∴四边形DEFG是平行四边形.
(2)∵∠OBC和∠OCB互余,
∴∠BOC=90°.
∵M为EF的中点,OM=2,
∴EF=2OM=4,∴BC=2EF=8.
12. 如图18-1-59,在△ABC中,AB=AC,点D,
E分别是边AB,AC的中点,连接DE,BE,点F,
G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.
【C组】
(1)证明:∵AB=AC,点D,E分别是边AB,AC
的中点,∴BD=EC.
∵点F,G,H分别为BE,DE,BC的中点,
∴FG∥BD,FG= BD,FH∥EC,FH= EC.
∴FG=FH.
(2)证明:由(1)得FG∥BD.
又∵∠A=90°,∴FG⊥AC.
∵FH∥EC,∴FG⊥FH.
(3)解:如答图18-1-6,
延长FG交AC于点K.
∵FG∥BD,∠A=80°,
∴∠FKC=∠A=80°.
∵FH∥EC,
∴∠GFH=180°-∠FKC=100°.
相关文档
- 八年级道德与法治上册第一单元走进2021-11-0119页
- 人教部编版八年级下册道德与法治教2021-11-0132页
- 人教版八年级数学上册第十二章全等2021-11-0122页
- 八年级道德与法治上册第二单元遵守2021-11-0121页
- 八年级道德与法治上册第四单元维护2021-11-0119页
- 人教版八年级数学上册第十二章全等2021-11-0123页
- 2018_2019学年八年级数学上册第五2021-11-0113页
- 2019版八年级历史下册第五单元国防2021-11-0132页
- 八年级数学上册第2章三角形2-5全等2021-11-0118页
- 最新部编版八年级上册道德与法治课2021-11-01442页