2020八年级数学下册 第十七章《勾股定理》练习（无答案）（新版）新人教版 6页

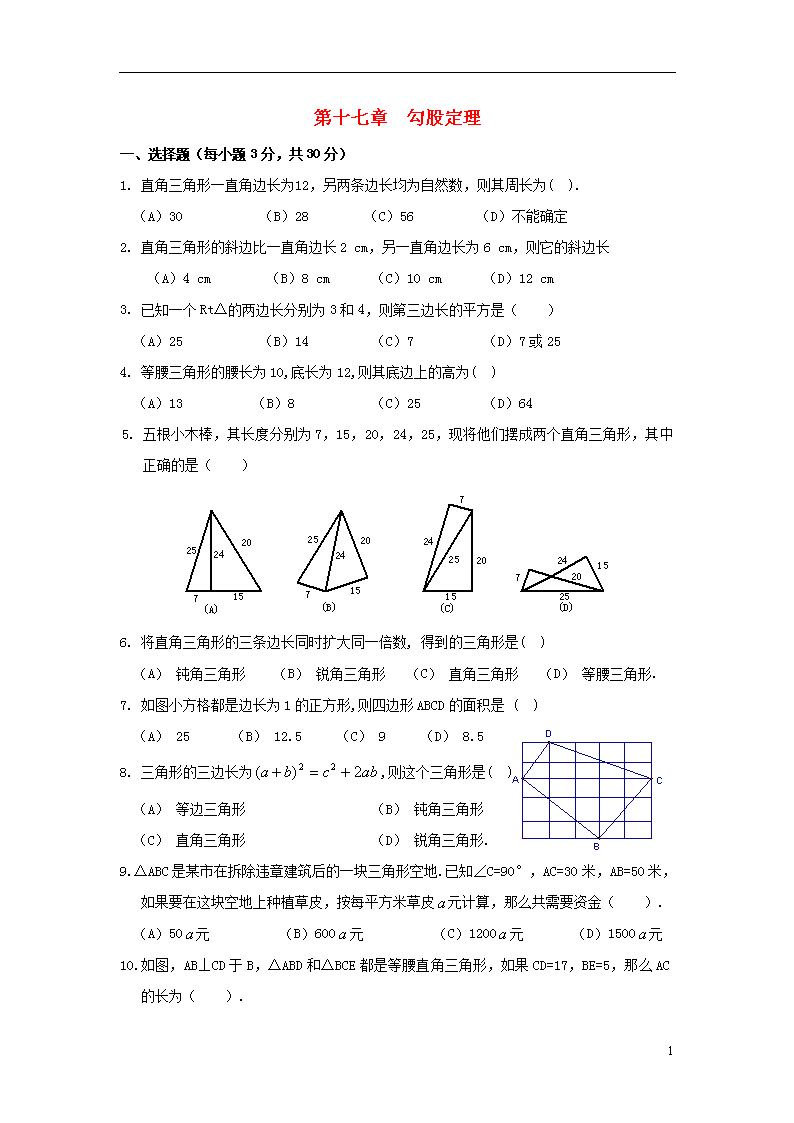
第十七章 勾股定理 ‎ 一、选择题（每小题3分，共30分）‎ ‎1. 直角三角形一直角边长为12，另两条边长均为自然数，则其周长为( ).‎ ‎（A）30 （B）28 （C）56 （D）不能确定 ‎2. 直角三角形的斜边比一直角边长‎2 cm，另一直角边长为‎6 cm，则它的斜边长 ‎（A）‎4 cm （B）‎8 cm （C）‎10 cm （D）‎‎12 cm ‎3. 已知一个Rt△的两边长分别为3和4，则第三边长的平方是（　　）‎ ‎ （A）25 （B）14 （C）7 （D）7或25‎ ‎4. 等腰三角形的腰长为10,底长为12,则其底边上的高为( ) ‎ ‎（A）13 （B）8 （C）25 （D）64‎ ‎5. 五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（ ） ‎ ‎6. 将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )‎ ‎（A） 钝角三角形 （B） 锐角三角形 （C） 直角三角形 （D） 等腰三角形.‎ ‎7. 如图小方格都是边长为1的正方形,则四边形ABCD的面积是 ( )‎ ‎（A） 25 （B） 12.5 （C） 9 （D） 8.5‎ ‎8. 三角形的三边长为,则这个三角形是( )‎ ‎（A） 等边三角形 （B） 钝角三角形 ‎ ‎（C） 直角三角形 （D） 锐角三角形.‎ ‎9.△ABC是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°，AC=‎30米，AB=‎50米，如果要在这块空地上种植草皮，按每平方米草皮元计算，那么共需要资金（ ）.‎ ‎（A）50元 （B）600元 （C）1200元 （D）1500元 ‎10.如图，AB⊥CD于B，△ABD和△BCE都是等腰直角三角形，如果CD=17，BE=5，那么AC的长为（ ）.‎ 6‎ ‎（A）12 （B）7 （C）5 （D）13‎ E A B C D ‎ ‎ ‎ （第10题） （第11题） （第14题）‎ 二、填空题（每小题3分，24分）‎ ‎11. 如图为某楼梯,测得楼梯的长为‎5米,高‎3米,计划在楼梯表面铺地毯,地毯的长度至少需要____________米.‎ ‎12. 在直角三角形中，斜边=2，则=______.‎ ‎13. 直角三角形的三边长为连续偶数，则其周长为 .‎ ‎14. 如图，在△ABC中，∠C=90°，BC=3，AC=4.以斜边AB为直径作半圆，则这个半圆的面积是____________.‎ ‎ ‎ ‎ （第15题） （第16题） （第17题）‎ ‎15. 如图，校园内有两棵树，相距‎12米，一棵树高‎13米，另一棵树高‎8米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞___________米.‎ A B C D 第18题图 ‎7cm ‎16. 如图，△ABC中，∠C=90°，AB垂直平分线交BC于D若BC=8，AD=5，则AC等于______________.‎ ‎17. 如图，四边形是正方形，垂直于，且=3，=4，阴影部分的面积是______.‎ ‎18. 如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边和长为‎7cm,则正方形A，B，C，D的面积之和为___________cm2.‎ 6‎ 三、解答题（每小题8分，共40分）‎ ‎19. 11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题：‎ ‎“小溪边长着两棵棕榈树，恰好隔岸相望.一棵树高是30肘尺（肘尺是古代的长度单位），另外一棵高20肘尺；两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然，两只鸟同时看见棕榈树间的水面上游出一条鱼，它们立刻飞去抓鱼，并且同时到达目标.问这条鱼出现的地方离开比较高的棕榈树的树跟有多远？‎ ‎20. 如图，已知一等腰三角形的周长是16，底边上的高是4.求这个三角形各边的长.‎ ‎　　　　‎ ‎21. 如图，A、B两个小集镇在河流CD的同侧，分别到河的距离为AC=10千米，BD=30千米，且CD=30千米，现在要在河边建一自来水厂，向A、B两镇供水，铺设水管的费用为每千米3万，请你在河流CD上选择水厂的位置M，使铺设水管的费用最节省，并求出总费用是多少？‎ A B C D L 第21题图 ‎22. 如图所示的一块地，∠ADC=90°，AD=‎12m，CD=‎9m，AB=‎39m，BC=‎36m，求这块地的面积。‎ 6‎ ‎23. 如图，一架‎2.5米长的梯子AB，斜靠在一竖直的墙AC上，这时梯足B到墙底端C的距离为‎0.7米，如果梯子的顶端沿墙下滑‎0.4米，那么梯足将向外移多少米？‎ 四、综合探索（共26分）‎ ‎24.（12分）如图，某沿海开放城市A接到台风警报，在该市正南方向‎100km的B处有一台风中心，沿BC方向以‎20km/h的速度向D移动，已知城市A到BC的距离AD=‎60km，那么台风中心经过多长时间从B点移到D点？如果在距台风中心‎30km的圆形区域内都将有受到台风的破坏的危险，正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险？‎ A B C D 第24题图 ‎25.（14分）△ABC中，BC，AC，AB，若∠C=90°，如图（1），根据勾股定理，则，若△ABC不是直角三角形，如图（2）和图（3），请你类比勾股定理，试猜想与的关系，并证明你的结论.‎ 6‎ 参考答案如下 一、选择题（每小题3分，共30分）‎ ‎1.（D）；2.（C）；3.（D）；4.（B）；5.（C）；‎ ‎6.（C）；7.（B）；8.（C）；9.（B）；10.（D）；‎ 二、填空题（每小题3分，24分）‎ ‎11.7；12.8；13.24；14.； 15. 13；‎ ‎16.4；17.19；18.49；‎ 三、解答题 ‎19.20；‎ ‎20. 设BD=x，则AB=8-x ‎　　　由勾股定理，可以得到AB2=BD2+AD2，也就是(8-x)2=x2+42.‎ ‎　　　所以x=3，所以AB=AC=5，BC=6‎ ‎21.作A点关于CD的对称点A′，连结B A′，与CD交于点E，则E点即为所求.总费用150万元.‎ ‎22.116m2‎‎；‎ ‎23. ‎0.8‎米‎；‎ 四、综合探索 ‎24.4小时，2.5小时.‎ ‎25. 解：若△ABC是锐角三角形，则有a2+b2>c2 ‎ 若△ABC是钝角三角形，∠C为钝角，则有a2+b20，x>0‎ ‎∴2ax>0‎ ‎∴a2+b2>c2 ‎ 当△ABC是钝角三角形时，‎ 证明：过点B作BDAC，交AC的延长线于点D.‎ 设CD为x，则有DB2=a2－x2 ‎ 根据勾股定理得 (b＋x)2＋a2―x 2＝c2‎ 即 b2＋2bx＋x2＋a2―x 2＝c2‎ ‎∴a2＋b2＋2bx＝c2 ‎ ‎∵b>0，x>0‎ ‎∴2bx>0‎ ‎∴a2+b2