北师大版八年级数学（下册）第一章测试卷（附答案） 12页

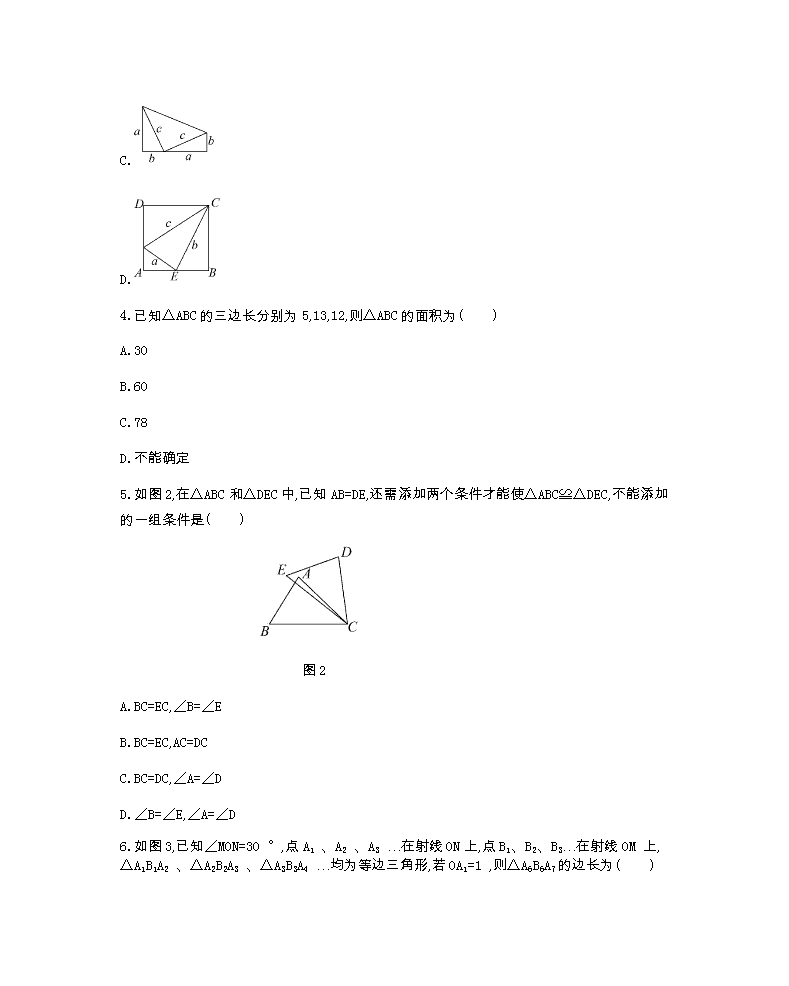
北师八下数学测试卷第一章 ‎ ‎1.下列说法错误的是(　　)‎ A.斜边和一锐角对应相等的两个直角三角形全等 B.有两边对应角相等的两个直角三角形全等 C.有两个锐角相等的两个直角三角形全等 D.有一直角边和一锐角对应相等的两个直角三角形全等 ‎2.如图1,∠C=90°,DE垂直平分AB,DC=DE,则∠ADC的度数为(　　)‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　图1‎ A.40°‎ B.50°‎ C.60°‎ D.70°‎ ‎3.下列选项中,不能用来证明勾股定理的是(　　)‎ A.‎ B.‎ C.‎ D.‎ ‎4.已知△ABC的三边长分别为5,13,12,则△ABC的面积为(　　)‎ A.30‎ B.60‎ C.78‎ D.不能确定 ‎5.如图2,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是(　　)‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　图2‎ A.BC=EC,∠B=∠E B.BC=EC,AC=DC C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D ‎6.如图3,已知∠MON=30 °,点A1 、A2 、A3 …在射线ON上,点B1、B2、B3…在射线OM 上,△A1B1A2 、△A2B2A3 、△A3B3A4 …均为等边三角形,若OA1=1 ,则△A6B6A7的边长为(　　)‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　图3‎ A.6‎ B.12‎ C.32‎ D.64‎ ‎7.已知：在△ABC中,∠A=60°,如要判定△ABC是等边三角形,还需添加一个条件.现有下面三种说法：‎ ‎①如果添加条件“AB=AC”,那么△ABC是等边三角形;‎ ‎②如果添加条件“∠B=∠C”,那么△ABC是等边三角形;‎ ‎③如果添加条件“边AB、BC上的高相等”,那么△ABC是等边三角形.‎ 上述说法中,正确的说法有(　　)‎ A.3个 B.2个 C.1个 D.0个 ‎8.如图4,在△ABC中,AB=AC,E是AB的中点,以点E为圆心,EB为半径画弧,交BC于点D,连接ED并延长到点F,使DF=DE,连接FC,若∠B=70°,则∠F的度数是(　　)‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　图4‎ A.40°‎ B.70°‎ C.50°‎ D.45°‎ ‎9.已知一个三角形的边长分别是6 cm,8 cm,10 cm,则它的面积是　　　　　　　　cm2.‎ ‎10.若A、B、C为三个正整数,且A+B+C=12,则以A、B、C为边所组成的三角形可以是：①等腰三角形;②等边三角形;③直角三角形,你认为以上符合条件的正确结论的序号是　　　　　　　　　.‎ ‎11.如图5,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为　　　　　　　　　.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　图5‎ ‎12.如图6,∠AOB=30°,OP平分∠AOB,PC∥OB,PD⊥OB,如果PC=6,那么PD等于　　　　　　　.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　图6‎ ‎13.如图7,MN∥PQ,AB⊥PQ,点A、D和点B、C分别在直线MN与PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=　　　　　　　　.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　图7‎ ‎14.如图8,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成△PAB,△PBC,△PAC均是等腰三角形,则满足上述条件的所有点P的个数为　　　　　　　　个.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　图8‎ ‎15.如图9,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.‎ 求证：(1)PE=PF;‎ ‎(2)点P在∠BAC的角平分线上.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　图9‎ ‎16.如图10,在△ABC中,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F.求证：AD垂直平分EF.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　图10‎ ‎17.已知：如图11,在Rt△ABC中,∠A=90°,CD平分∠ACB交边AB于点D,DE⊥BC,垂足为E,AD=BD.求证：BE=CE.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　图11‎ ‎18.如图12,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.‎ ‎(1)求证：BE=CE;‎ ‎(2)如图13,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其他条件不变.求证：△AEF≌△BCF.‎ ‎　　　　　　　　　　　　‎ ‎　　　　　　　　　　图12　　　　　　　　图13‎ ‎19.如图14,△ABC为正三角形,D为边BA延长线上一点,连接CD,以CD为一边作正三角形CDE,连接AE,判断AE与BC的位置关系,并说明理由.‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　图14‎ ‎20.(1)如图15是一个重要公式的几何解释,请你写出这个公式;‎ ‎(2)伽菲尔德(1881年任美国第20届总统)利用(1)中的公式和图16证明了勾股定理(1876年4月1日发表在《新英格兰教育日志》上),现请你尝试写出证明过程,说明：c2=a2+b2.‎ ‎　　　　　　　　　　　　‎ ‎　　　　　　　　　图15　　　　　　　　　　　图16‎ 参考答案 ‎1.C ‎2.C ‎3.D ‎4.A ‎5.C ‎6.C ‎7.A ‎8.A ‎9.24‎ ‎10.①②③‎ ‎11.13‎ ‎12.3‎ ‎13.7‎ ‎14.6‎ ‎15.证明：(1)如图,连接AP并延长.‎ ‎　　　　　　 ‎ ‎∵PE⊥AB,PF⊥AC,‎ ‎∴∠AEP=∠AFP=90°.‎ 又AE=AF,AP=AP,‎ ‎∵在Rt△AFP和Rt△AEP中,‎ ‎∴Rt△AEP≌Rt△AFP(HL).‎ ‎∴PE=PF.‎ ‎(2)∵Rt△AEP≌Rt△AFP,‎ ‎∴∠EAP=∠FAP.‎ ‎∴AP是∠BAC的角平分线.‎ 故点P在∠BAC的角平分线上.‎ ‎16.证明：∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,‎ ‎∴DE=DF,∠AED=∠AFD=90°.‎ 在Rt△AED和Rt△AFD中,‎ ‎∴Rt△AED≌Rt△AFD(HL),‎ ‎∴AE=AF.‎ ‎∵AD是∠BAC的平分线,‎ ‎∴AD垂直平分EF(三线合一).‎ ‎17.证明：∵∠A=90°,DE⊥BC,CD平分∠ACB,‎ ‎∴AD=DE.‎ ‎∵AD=BD,‎ ‎∴DE=BD.‎ 在Rt△BDE中,∵DE=BD,‎ ‎∴∠B=30°.‎ 在Rt△ABC中,‎ ‎∵∠A=90°,∠B=30°,‎ ‎∴∠ACB=60°.‎ ‎∵CD平分∠ACB,‎ ‎∴∠BCD=∠ACB=30°.‎ ‎∴∠BCD=∠B,‎ ‎∴BD=CD.‎ ‎∵DE⊥BC,‎ ‎∴BE=CE.‎ ‎18.证明：(1)∵AB=AC,D是BC的中点,‎ ‎∴∠BAE=∠EAC.‎ 在△ABE和△ACE中,‎ ‎∴△ABE≌△ACE(SAS).‎ ‎∴BE=CE.‎ ‎(2)∵∠BAC=45°,BF⊥AF,‎ ‎∴△ABF为等腰直角三角形.‎ ‎∴AF=BF.‎ ‎∵AB=AC,点D是BC的中点,‎ ‎∴AD⊥BC.‎ ‎∴∠EAF+∠C=90°.‎ ‎∵BF⊥AC,‎ ‎∴∠CBF+∠C=90°.‎ ‎∴∠EAF=∠CBF.‎ 在△AEF和△BCF中,‎ ‎∴△AEF≌△BCF(ASA).‎ ‎19.解：AE∥BC.理由如下：‎ ‎∵△ABC与△CDE为正三角形,‎ ‎∴BC=AC,CD=CE,∠ACB=∠DCE=60°.‎ ‎∴∠ACB+∠ACD=∠DCE+∠ACD,‎ 即∠BCD=∠ACE.‎ ‎∴△BCD≌△ACE.‎ ‎∴∠B=∠EAC.‎ ‎∵∠B=∠ACB,‎ ‎∴∠EAC=∠ACB.‎ ‎∴AE∥BC.‎ ‎20.解：(1)(a+b)2=a2+2ab+b2;‎ ‎(2)∵Rt△DEC≌Rt△EAB,‎ ‎∴∠DEC=∠EAB.‎ ‎∵∠EAB+∠AEB=90°,‎ ‎∴∠DEC+∠AEB=90°.‎ ‎∴△AED为等腰直角三角形.‎ ‎∵S梯形ABCD=SRt△ABE+SRt△DCE+SRt△DEA,‎ ‎∴(b+a)(a+b)=ab + ab + c2,即(a+b)2=2ab+c2,‎ ‎∵(a+b)2=a2+2ab+b2,‎ ‎∴a2+2ab+b2=2ab+c2,‎ ‎∴c2=a2+b2.‎