八年级数学下册知能提升作业二十第19章全等三角形19 5页

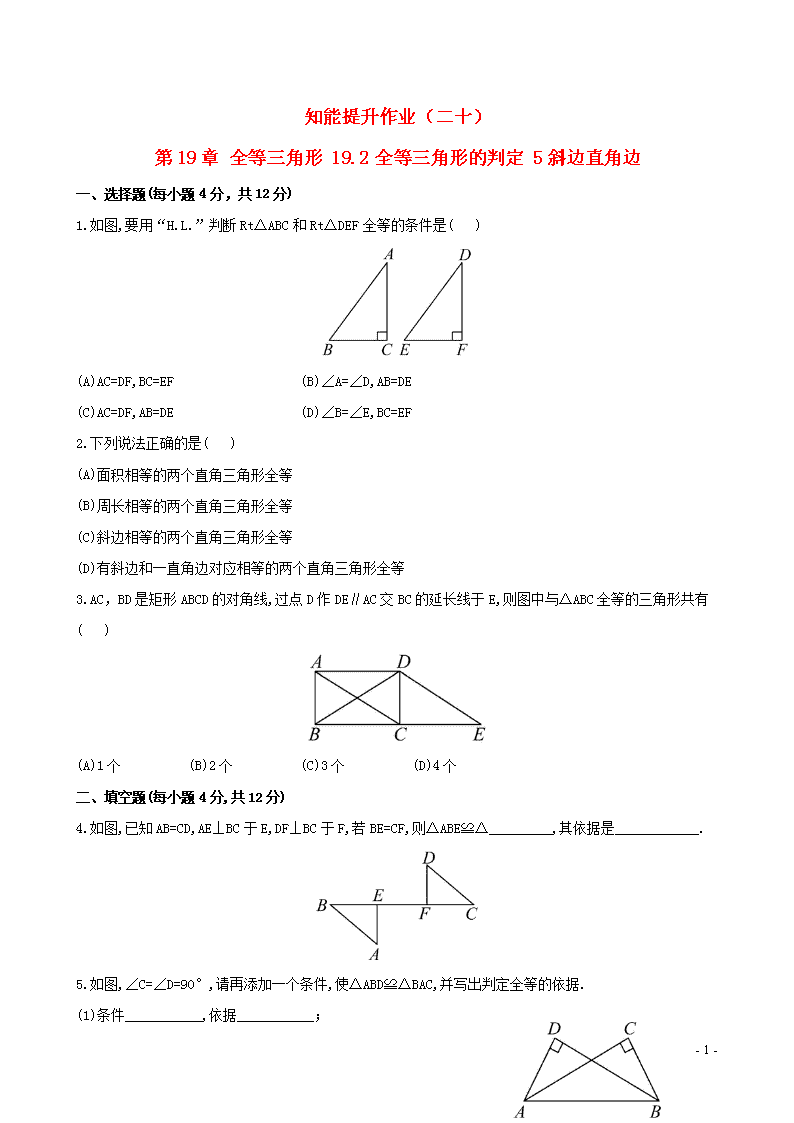
知能提升作业（二十）‎ 第19章 全等三角形 19.2全等三角形的判定 5斜边直角边 ‎ 一、选择题(每小题4分，共12分)‎ ‎1.如图,要用“H.L.”判断Rt△ABC和Rt△DEF全等的条件是( )‎ ‎(A)AC=DF,BC=EF (B)∠A=∠D,AB=DE ‎(C)AC=DF,AB=DE (D)∠B=∠E,BC=EF ‎ ‎2.下列说法正确的是( )‎ ‎(A)面积相等的两个直角三角形全等 ‎(B)周长相等的两个直角三角形全等 ‎(C)斜边相等的两个直角三角形全等 ‎(D)有斜边和一直角边对应相等的两个直角三角形全等 ‎3.AC，BD是矩形ABCD的对角线,过点D作DE∥AC交BC的延长线于E,则图中与△ABC全等的三角形共有( )‎ ‎(A)1个 (B)2个 (C)3个 (D)4个 二、填空题(每小题4分,共12分)‎ ‎4.如图,已知AB=CD,AE⊥BC于E,DF⊥BC于F,若BE=CF,则△ABE≌△_________,其依据是____________.‎ ‎5.如图,∠C=∠D=90°,请再添加一个条件,使△ABD≌△BAC,并写出判定全等的依据.‎ ‎(1)条件___________,依据___________；‎ - 5 -‎ ‎(2)条件___________,依据___________；‎ ‎(3)条件___________,依据___________；‎ ‎(4)条件___________,依据___________.‎ ‎6.(2011·郴州中考)如图,已知∠1=∠2=90°,AD=EA,那么图中有______对全等三角形.‎ 三、解答题(共26分)‎ ‎7.(8分)如图,AE⊥BC,DF⊥BC,E,F是垂足,且AE=DF,AB=DC,求证:∠ABC=∠DCB.‎ ‎8.(8分)如图，已知：AB=AC,CD⊥AB于点D,BE⊥AC于点E，CD，BE交于点O，求证：AO平分∠BAC.‎ ‎【拓展延伸】‎ ‎9.(10分)已知,如图1,E，F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点.‎ ‎(1)求证:MB=MD,ME=MF；‎ ‎(2)当E,F两点移动至如图2所示的位置时,其余条件不变,上述结论能否成立？若成立,请给出你的证明.若不成立,请说明你的理由.‎ - 5 -‎ 答案解析 ‎1.【解析】选C.∵在两个直角三角形中AB,DE是斜边,‎ ‎∴只有C中,AC=DF,AB=DE符合.故选C.‎ ‎2.【解析】选D.根据直角三角形全等的判定方法,选项A，B，C都不能保证两个直角三角形全等，选项D正确.‎ ‎3.【解析】选D.①∵AB=DC,∠ABC=∠CDA,BC=AD，‎ ‎∴△ABC≌△CDA；‎ ‎②∵AB=DC,∠ABC=∠DCB,BC=CB,‎ ‎∴△ABC≌△DCB；‎ ‎③∵AB=BA,∠ABC=∠BAD,BC=AD,‎ ‎∴△ABC≌△BAD；‎ ‎④∵DE∥AC,∴∠ACB=∠DEC.‎ 又∵AB=DC,∠ABC=∠DCE,∴△ABC≌△DCE.‎ ‎4.【解析】因为AE⊥BC,DF⊥BC,所以∠AEB=∠DFC=90°.在Rt△AEB和Rt△DFC中,AB=DC,BE=CF,所以依据H.L.得Rt△ABE≌Rt△DCF.‎ 答案：DCF H.L.‎ ‎5.【解析】在Rt△ABD和Rt△BAC中,已知∠C=∠D=90°,AB=BA；因此,(1)当AD=BC,可依据H.L.证明Rt△ABD≌Rt△BAC；(2)当∠DAB=∠CBA可依据A.A.S.证明 - 5 -‎ Rt△ABD≌Rt△BAC；(3)当DB=CA可依据H.L.证明Rt△ABD≌Rt△BAC；(4)当 ‎∠DBA=∠CAB可依据A.A.S.证明Rt△ABD≌Rt△BAC.‎ 答案：(1) AD=BC H.L.‎ ‎(2)∠DAB=∠CBA A.A.S.‎ ‎(3)DB=CA H.L. (4)∠DBA=∠CAB A.A.S.‎ ‎6.【解析】由∠1=∠2=90°,∠A=∠A, AD=AE,根据A.A.S.得△ADC≌△AEB；由∠BOD=∠COE,∠OBD=∠OCE,BD=CE(由△ADC≌△AEB，得AC=AB，又AD=EA,所以得BD=CE),根据A.A.S.得△BOD≌△COE；由BD=CE,∠OBD=∠ECO=90°,DE=ED,根据H.L.得△BDE≌△CED.‎ 答案：3‎ ‎7.【证明】∵AE⊥BC,DF⊥BC,‎ ‎∴∠AEB=∠DFC=90°,‎ 在Rt△ABE和Rt△DCF中,‎ AB=CD,‎ AE=DF,‎ ‎∴Rt△AEB≌Rt△DFC(H.L.),‎ ‎∴∠ABC=∠DCB.‎ ‎8.【证明】∵CD⊥AB,BE⊥AC,‎ ‎∴∠AEB=∠ADC=90°.‎ 在△ABE和△ACD中，‎ ‎∴△ABE≌△ACD(A.A.S.).‎ ‎∴AE=AD.‎ 在Rt△AOE和Rt△AOD中，‎ ‎∴Rt△AOE≌Rt△AOD(H.L.).‎ ‎∴∠OAD=∠OAE,‎ ‎∴AO平分∠BAC.‎ ‎9.【解析】(1)如图1,‎ ‎∵DE⊥AC,BF⊥AC,‎ - 5 -‎ ‎∴∠DEM=∠BFM=90°.‎ 在Rt△AFB和Rt△CED中,‎ ‎∵AB=CD,‎ AF=CE,‎ ‎∴Rt△AFB≌Rt△CED(H.L.),‎ ‎∴BF=DE；‎ 在△BFM和△DEM中,‎ ‎∵∠DEM=∠BFM,∠EMD=∠FMB,BF=DE,‎ ‎∴△BFM≌△DEM(A.A.S.),‎ ‎∴MB=MD,ME=MF；‎ ‎(2)当E,F两点移动至如图2位置时,其余条件不变,上述结论仍成立.这是因为Rt△AFB≌Rt△CED,△BFM≌△DEM的关系没有发生变化,因而结论MB=MD,ME=MF仍成立.‎ - 5 -‎