沪科版八年级数学上册第12章测试题（含答案） 11页

沪科版八年级数学上册第12章测试题（含答案）‎ ‎(考试时间：120分钟　　　满分：150分)‎ 分数：__________‎ 一、选择题(本大题共10小题，每小题4分，满分40分)‎ 每小题都给出A、B、C、D四个选项，其中只有一个是正确的．‎ ‎1．下列函数中是一次函数的是(　A　)‎ A．y＝ B．y＝ C．y＝ax＋b D．y＝x2‎ ‎2．在函数y＝中，自变量x的取值范围是(　A　)‎ A．x≠－3 B．x＞－3‎ C．x≤－3 D．x＜－3‎ ‎3．下列图象中，表示y不是x的函数的是(　B　)‎ ‎4．(宣城期末)一次函数y＝x＋3的图象不经过的象限是(　D　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎5．(蚌埠期末)关于直线y＝－2x，下列结论正确的是(　C　)‎ A．图象必过点(1，2)‎ B．图象经过第一、三象限 C．与y＝－2x＋1平行 11‎ D．y随x的增大而增大 ‎6．若点A(－1，a)，点B(－4，b)在一次函数y＝－5x－3图象上，则a与b的大小关系是(　A　)‎ A．a＜b B．a＞b C．a＝b D．无法确定 ‎7．若一次函数y＝(k－3)x－1的图象不经过第一象限，则(　A　)‎ A．k＜3 B．k＞3 C．k＞0 D．k＜0‎ ‎8．★一条直线与x轴交于点A(－4，0)，与y轴交于点B，若点B到x轴的距离为2，则该直线对应的函数表达式为(　C　)‎ A．y＝x＋2‎ B．y＝－x－2‎ C．y＝x＋2或y＝－x－2‎ D．y＝x＋2或y＝x－2‎ ‎9．★甲、乙两车从A城出发匀速行驶至B城，在整个行驶过程中，甲、乙两车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图所示．下列说法错误的是(　D　)‎ A．A，B两城相距300 km B．乙车比甲车晚出发1 h，却早到1 h C．乙车出发后1.5 h追上甲车 D．在一车追上另一车之前，当两车相距40 km时，t＝ ‎ ‎ 第9题图　　 第10题图 ‎10．★(肥西县期末)如图，点P是长方形ABCD边上一动点，沿A→D→C→B的路径移动，设P点经过的路径长为x，△BAP的面积是y，则下列能大致反映y与x的函数关系的图象是(　B　)‎ 11‎ ‎ ‎ A　　　　 B ‎ ‎ C　　　　 D 二、填空题(本大题共4小题，每小题5分，满分20分)‎ ‎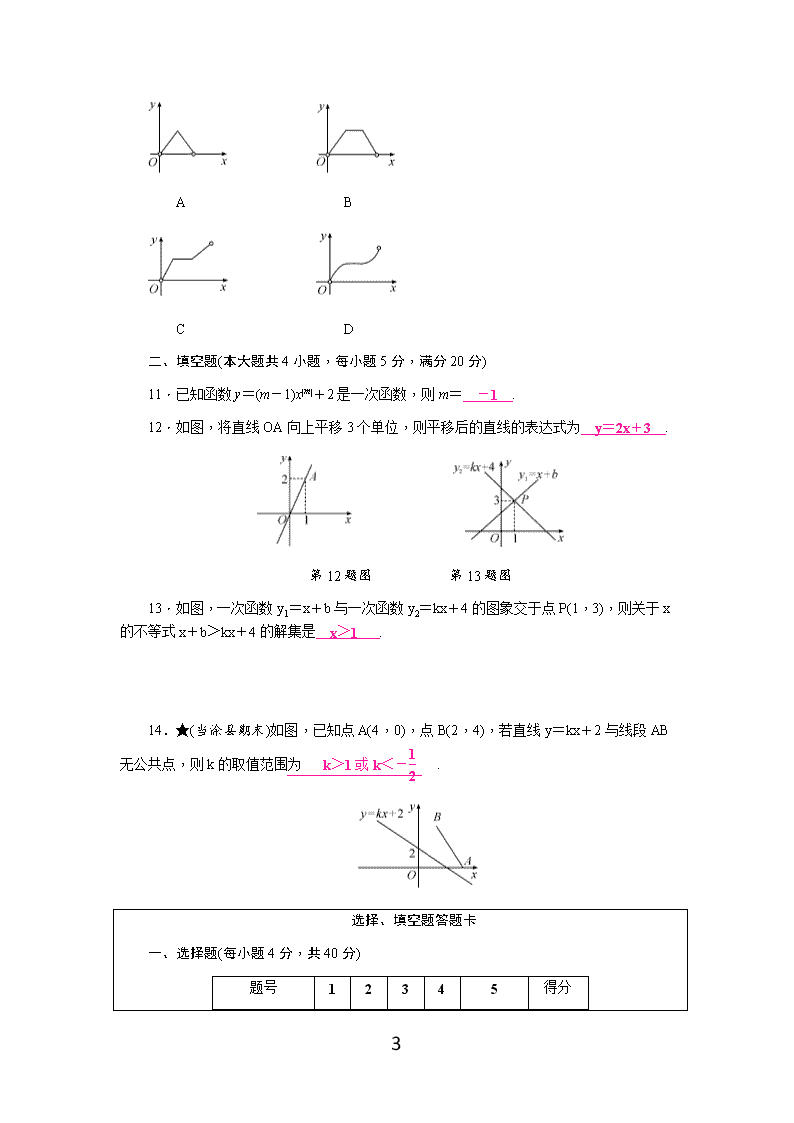11．已知函数y＝(m－1)x|m|＋2是一次函数，则m＝ －1 .‎ ‎12．如图，将直线OA向上平移3个单位，则平移后的直线的表达式为 y＝2x＋3 .‎ ‎ ‎ 第12题图　 第13题图 ‎13．如图，一次函数y1＝x＋b与一次函数y2＝kx＋4的图象交于点P(1，3)，则关于x的不等式x＋b＞kx＋4的解集是 x＞1 .‎ ‎14．★(当涂县期末)如图，已知点A(4，0)，点B(2，4)，若直线y＝kx＋2与线段AB无公共点，则k的取值范围为 k＞1或k＜－ .‎ ‎ ‎ 选择、填空题答题卡 一、选择题(每小题4分，共40分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 得分 11‎ 答案 A A B D C 题号 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 A A C D B 二、填空题(每小题5分，共20分)得分：______‎ ‎11．__－1__　12.__y＝2x＋3__　13.__x＞1__‎ ‎14． k＞1或k＜－ ‎ 三、(本大题共2小题，每小题8分，满分16分)‎ ‎15．(长丰县期末)一次函数图象经过(3，1)，(2，0)两点．‎ ‎(1)求这个一次函数的表达式；‎ ‎(2)求当x＝6时，y的值．‎ 解：(1)设一次函数表达式为y＝kx＋b.‎ 把(3，1)，(2，0)代入得解得 ‎∴一次函数的表达式为y＝x－2.‎ ‎(2)当x＝6时，y＝x－2＝6－2＝4.‎ ‎16．已知一次函数的图象平行于y＝－x，且截距为1.‎ ‎(1)求这个函数的表达式；‎ ‎(2)判断点P是否在这个函数的图象上．‎ 解：(1)设这个函数的表达式为y＝kx＋b.‎ ‎∵一次函数的图象平行于y＝－x，且截距为1，‎ ‎∴k＝－，b＝1，‎ ‎∴这个函数的表达式为y＝－x＋1.‎ ‎(2)当x＝－2时，y＝＋1＝≠，∴点P不在这个函数的图象上．‎ 11‎ 四、(本大题共2小题，每小题8分，满分16分)‎ ‎17．在所给的平面直角坐标系中，画出函数y＝2x＋4的图象，利用图象：‎ ‎(1)求方程2x＋4＝0的解；‎ ‎(2)求不等式2x＋4＜0的解；‎ ‎(3)若－2≤y≤6，求x的取值范围．‎ 解：当x＝0时，y＝4；‎ 当y＝0时，x＝－2，‎ ‎∴A(0，4)，B(－2，0)，‎ 作直线AB，如图所示．‎ ‎(1)由图象得：方程2x＋4＝0的解为x＝－2.‎ ‎(2)由图象得：不等式2x＋4＜0的解为x＜－2.‎ ‎(3)由图象得：－2≤y≤6时，x的取值范围为－3≤x≤1.‎ ‎18．已知，一次函数y＝(1－3k)x＋2k－1，试回答：‎ ‎(1)k为何值时，y是x的正比例函数？‎ ‎(2)当函数图象不经过第一象限时，求k的取值范围．‎ 解：(1)∵y是x的正比例函数，‎ ‎∴2k－1＝0，解得k＝，‎ ‎∴当k＝时，y是x的正比例函数．‎ ‎(2)当函数图象经过第二、四象限时，解得k＝；‎ 11‎ 当函数图象经过第二、三、四象限时，解得＜k＜.‎ ‎∴当函数图象不经过第一象限时，k的取值范围为＜k≤.‎ 五、(本大题共2小题，每小题10分，满分20分)‎ ‎19．已知一次函数y＝kx＋b的自变量的取值范围是－3≤x≤6，相应的函数值的取值范围是－5≤y≤－2，求这个一次函数的表达式．‎ 解：分两种情况：‎ ‎①当k＞0时，把x＝－3，y＝－5；x＝6，y＝－2代入一次函数的表达式y＝kx＋b，‎ 得解得 则这个函数的表达式是y＝x－4(－3≤x≤6)；‎ ‎②当k＜0时，把x＝－3，y＝－2；x＝6，y＝－5代入一次函数的表达式y＝kx＋b，‎ 得解得 则这个函数的表达式是y＝－x－3(－3≤x≤6)．‎ 故这个函数的表达式是y＝x－4(－3≤x≤6)或y＝－x－3(－3≤x≤6)．‎ ‎20．如图，直线y＝kx＋b(k≠0)与两坐标轴分别交于点B，C，点A的坐标为(－2，0)，点D的坐标为(1，0)．‎ ‎(1)求直线BC的函数表达式．‎ ‎(2)若P(x，y)是直线BC在第一象限内的一个动点，试求出△ADP的面积S与x的函数关系式，并写出自变量x的取值范围．‎ 11‎ 解：(1)设直线BC的函数关系式为y＝kx＋b(k≠0)，由图象可知：点C坐标是(0，4)，点B坐标是(6，0)，代入得 解得k＝－，b＝4，‎ 所以直线BC的函数关系式是y＝－x＋4.‎ ‎(2)∵点P(x，y)是直线BC在第一象限内的点，‎ ‎∴y＞0，y＝－x＋4，0＜x＜6，‎ ‎∵点A的坐标为(－2，0)，点D的坐标为(1，0)，‎ ‎∴AD＝3，‎ ‎∴S△ADP＝×3×＝－x＋6，‎ 即S＝－x＋6(0＜x＜6)．‎ ‎(3)在直线BC上是否存在一点P，使得△ADP的面积为3？若存在，请直接写出此时点P的坐标，若不存在，请说明理由．‎ 解：存在．当S＝3时，－x＋6＝3，‎ 解得x＝3，y＝－×3＋4＝2，‎ 即此时点P的坐标是(3，2)，‎ 根据对称性可知当点P在x轴下方时，可得满足条件的点P′(9，－2)．‎ 综上所述，点P的坐标为(3，2)或(9，－2)．‎ 六、(本题满分12分)‎ ‎21．如图①所示，某乘客乘高速列车从甲地经过乙地到丙地，列车匀速行驶，图②为列车离乙地的距离y(千米)与行驶时间x(小时)的函数关系图象．‎ 11‎ ‎(1)填空：甲、丙两地距离________千米；‎ ‎(2)求高速列车离乙地的距离y与行驶时间x之间的函数关系式，并写出x的取值范围．‎ 解：(1)根据函数图形可得，甲、丙两地距离为900＋150＝1 050(千米)，故答案为1 050.‎ ‎(2)当0≤x≤3时，设高速列车离乙地的距离y与行驶时间x之间的函数关系式为y＝kx＋b，‎ 把(0，900)，(3，0)代入得 解得 高速列车的速度为900÷3＝300(千米/时)，‎ ‎150÷300＝0.5(小时)，3＋0.5＝3.5(小时)，‎ 则点A的坐标为(3.5，150)．‎ ‎∴y＝－300x＋900，‎ 当3＜x≤3.5时，设高速列车离乙地的距离y与行驶时间x之间的函数关系式为y＝k1x＋b1，‎ 把(3，0)，(3.5，150)代入得 解得 ‎∴y＝300x－900，‎ ‎∴y＝ 11‎ 七、(本题满分12分)‎ ‎22．某学校计划租用8辆客车送280名师生参加社会实践活动，现有甲、乙两种客车，它们的载客量和租金如表，设租用甲种客车x辆，租车总费用为w元．‎ 甲种客车 乙种客车 载客量(人/辆)‎ ‎30‎ ‎40‎ 租金(元/辆)‎ ‎270‎ ‎320‎ ‎(1)求出w(元)与x(辆)之间的函数关系式，并直接写出自变量x的取值范围；‎ ‎(2)选择怎样的租车方案所需的费用最低？最低费用是多少元？‎ 解：(1)由题意可得，‎ ‎∵租用甲种客车x辆，‎ ‎∴租用乙种客车(8－x)辆，‎ w＝270x＋320(8－x)＝－50x＋2 560，‎ ‎∵30x＋40(8－x)≥280，‎ ‎∴x≤4，‎ 即w(元)与x(辆)之间的函数关系式是 w＝－50x＋2 560(0≤x≤4且x为整数)．‎ ‎(2)∵w＝－50x＋2 560，0≤x≤4且x为整数，‎ ‎∴当x＝4时，w取得最小值，‎ 此时8－x＝4，‎ w＝－50×4＋2 560＝2 360，‎ 答：当租用甲种客车4辆、乙种客车4辆时，总费用最低，最低费用是2 360元．‎ 八、(本题满分14分)‎ ‎23．在购买某场足球赛门票时，设购买门票数为x(张)，总费用为y(元)．现有两种购买方案：‎ 方案一：若单位赞助广告费10 000元，则该单位所购门票的价格为每张60元；(总费用＝广告赞助费＋门票费)‎ 方案二：购买门票方式如图所示．解答下列问题：‎ ‎(1)方案一中，y与x的函数关系式为________；方案二中，当0≤x≤100时，y 11‎ 与x的函数关系式为________；当x＞100时，y与x的函数关系式为________；‎ ‎(2)如果购买本场足球赛超过100张，你将选择哪一种方案，使总费用最省？请说明理由；‎ ‎(3)甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张，花费总费用计58 000元，求甲、乙两单位各购买门票多少张？‎ 解：(1)方案一：y＝60x＋10 000；‎ 方案二：当0≤x≤100时，y＝100x；‎ 当x＞100时，y＝80x＋2 000.‎ 故答案为：y＝60x＋10 000；‎ y＝100x；y＝80x＋2 000.‎ ‎(2)∵x＞100，∴方案二中y与x的函数关系式为 y＝80x＋2 000；‎ ‎∵方案一中y与x的函数关系式为 y＝60x＋10 000，‎ ‎∴当60x＋10 000＞80x＋2 000时，即x＜400时，选方案二进行购买；‎ 当60x＋10 000＝80x＋2 000时，即x＝400时，两种方案都可以；‎ 当60x＋10 000＜80x＋2 000时，即x＞400时，选方案一进行购买．‎ ‎(3)设甲、乙单位购买本次足球赛门票数分别为a张、b张．‎ ‎∵甲、乙单位分别采用方案一和方案二购买本次足球比赛门票，‎ ‎∴乙公司购买本次足球赛门票有两种情况：‎ ‎0＜b≤100或b＞100.‎ 当b≤100时，乙公司购买本次足球赛门票费为100b， 解得不符合题意，舍去；‎ 11‎ 当b＞100时，乙公司购买本次足球赛门票费为 ‎80b＋2 000，‎ 解得符合题意．‎ 答：甲、乙两单位购买本次足球赛门票数分别为500张、200张．‎ 11‎