八年级下册数学同步练习4-4 用待定系数法确定一次函数表达式1 湘教版 5页

‎4.4 用待定系数法确定一次函数表达式 要点感知 通过先设定函数表达式(确定函数模型)，再根据条件确定表达式中的未知系数，从而求出函数的表达式的方法称为__________法.在求一次函数y=kx+b(k，b为常数，k≠0)的表达式时，关键是要确定________、________的值.‎ 预习练习1-1 已知一次函数y=kx+k-3的图象经过点(2，3)，则k的值为__________.‎ ‎1-2 如果正比例函数y=kx的图象经过点(1，-2)，那么k的值等于__________.‎ 知识点1 用待定系数法求一次函数解析式 ‎1.若正比例函数的图象经过点(-1，2)，则这个图象必经过点( )‎ ‎ A.(1，2) B.(-1，-2) C.(2，-1) D.(1，-2)‎ ‎2.若点(3，1)在一次函数y＝kx-2(k≠0)的图象上，则k的值是( )‎ ‎ A.5 B.4 C.3 D.1‎ ‎3.直线y=kx+b经过点A(0，3)，B(-2，0)，则k的值为( )‎ ‎ A.3 B. C. 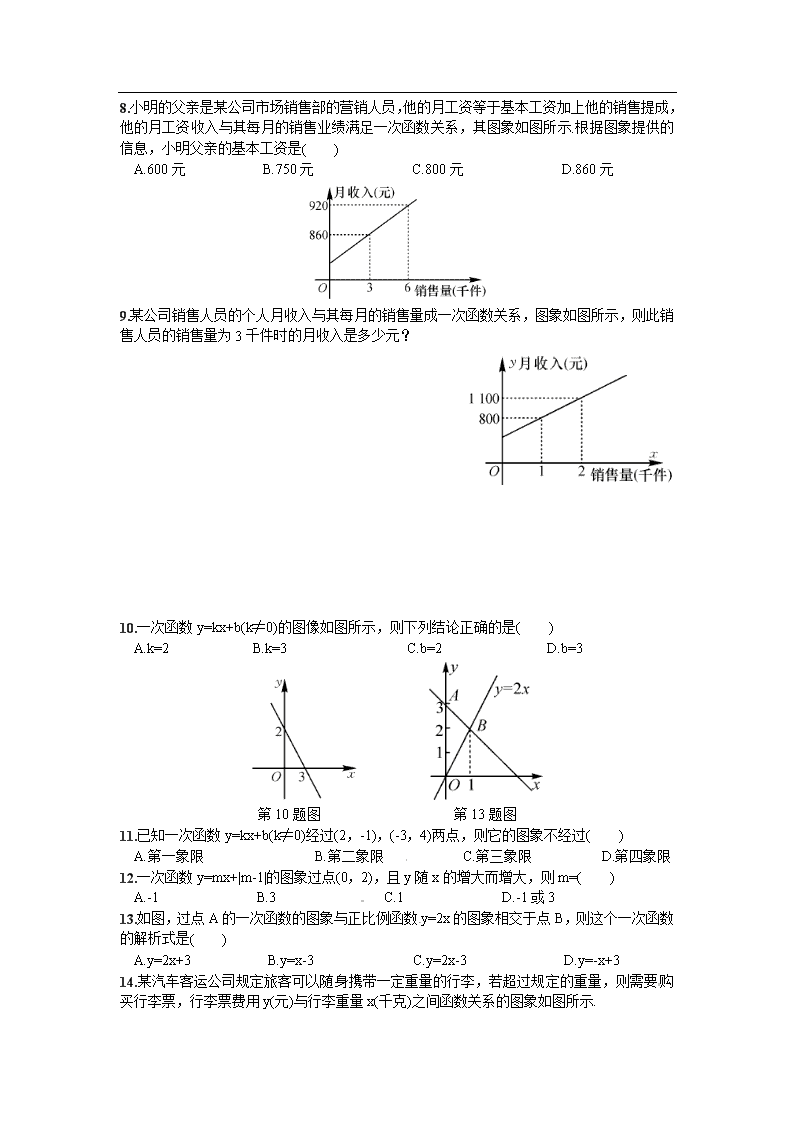D.-‎ ‎4.如图，直线AB对应的函数表达式是( )‎ ‎ A.y=-x+3 B.y=x+3 ‎ ‎ C.y=-x+3 D.y=x+3‎ ‎5.直线l过点M(-2,0)，该直线的解析式可以写为_________________(只写出一个即可).‎ ‎6.一次函数y=3x+b的图象过坐标原点，则b的值为__________.‎ ‎7.设一次函数y=kx+b(k≠0)的图象经过A(1，3)，B(0，-2)两点，试求k，b的值.‎ 知识点2 利用一次函数表达式解决实际问题 ‎8.小明的父亲是某公司市场销售部的营销人员，他的月工资等于基本工资加上他的销售提成，他的月工资收入与其每月的销售业绩满足一次函数关系，其图象如图所示.根据图象提供的信息，小明父亲的基本工资是( )‎ ‎ A.600元 B.750元 C.800元 D.860元 ‎9.某公司销售人员的个人月收入与其每月的销售量成一次函数关系，图象如图所示，则此销售人员的销售量为3千件时的月收入是多少元？‎ ‎[来源:学科网]‎ ‎10.一次函数y=kx+b(k≠0)的图像如图所示，则下列结论正确的是( )‎ ‎ A.k=2 B.k=3 C.b=2 D.b=3‎ ‎ ‎ 第10题图 第13题图[来源:Zxxk.Com]‎ ‎11.已知一次函数y=kx+b(k≠0)经过(2，-1)，(-3，4)两点，则它的图象不经过( )[来源:学科网]‎ ‎ A.第一象限 B.第二象限 C.第三象限 D.第四象限 ‎12.一次函数y=mx+|m-1|的图象过点(0，2)，且y随x的增大而增大，则m=( )‎ ‎ A.-1 B.3 C.1 D.-1或3‎ ‎13.如图，过点A的一次函数的图象与正比例函数y=2x的图象相交于点B，则这个一次函数的解析式是( )‎ ‎ A.y=2x+3 B.y=x-3 C.y=2x-3 D.y=-x+3‎ ‎14.某汽车客运公司规定旅客可以随身携带一定重量的行李，若超过规定的重量，则需要购买行李票，行李票费用y(元)与行李重量x(千克)之间函数关系的图象如图所示.‎ ‎ (1)求y与x之间的函数关系式；‎ ‎ (2)旅客最多可以免费携带多少千克的行李？‎ ‎15.在直角坐标系xOy中，直线l过(1，3)和(3，1)两点，且与x轴、y轴分别交于A，B两点.‎ ‎ (1)求直线l的函数表达式；‎ ‎ (2)求△AOB的面积.‎ ‎16.一次函数y=kx+b，当3≤x≤4时，3≤y≤6，则的值是__________.‎ ‎17.一个有进水管与出水管的容器，从某时刻开始的3分钟内只进水不出水，在随后的9分钟内既进水又出水，每分钟的进水量和出水量都是常数.容器内的水量y(单位：升)与时间x(单位：分)之间的关系如图所示.当容器内的水量大于5升时，求时间x的取值范围.‎ ‎[来源:学科网ZXXK]‎ ‎[来源:Zxxk.Com]‎ 参考答案 要点感知 待定系数 k b 预习练1-1 2‎ ‎1-2 -2‎ ‎1.D 2.D 3.B 4.A 5.答案不唯一，如y=x+2 6.0‎ ‎7.把A(1，3)，B(0，-2)代入y=kx+b得 ‎ 解得 ‎ 故k，b的值分别为5，-2.‎ ‎8.C ‎9.设直线解析式为y=kx+b，因图象过(1，800)，(2，1 100)，‎ ‎ ∴解得 ‎ ∴解析式为y=300x+500，‎ ‎ 当x=3时y=1 400.‎ ‎ 答：此销售人员的销售量为3千件时的月收入是1 400元.‎ ‎10.C 11.C 12.B 13.D ‎14.(1)设一次函数y=kx+b（k≠0），‎ ‎∵当x=60时，y=6，当x=90时，y=10，‎ ‎∴解得 ‎∴所求函数表达式为y=x-2(x≥15).‎ ‎ (2)当y=0时，x-2=0，∴x=15.‎ 故旅客最多可免费携带15千克行李.‎ ‎15.(1)设直线l的函数表达式为y=kx+b(k≠0)，把(3，1)，(1，3)代入，得 解得 ‎∴直线l的函数表达式为y=-x+4.‎ ‎ (2)当x=0时，y=4，‎ ‎∴B(0，4).‎ 当y=0，-x+4=0.解得x=4,‎ ‎∴A(4，0).‎ ‎∴S△AOB=AO·BO=×4×4=8.‎ ‎16.-2或-5‎ ‎17.①0≤x＜3时，‎ 设y=mx，则3m=15，解得m=5.‎ 所以，y=5x；‎ 当y=5时，x=1.‎ ‎ ②3≤x≤12时，‎ 设y=kx+b(k≠0)，‎ ‎∵函数图象经过点(3，15)，(12，0)，‎ ‎∴解得 ‎∴y=-x+20.‎ 当y=5时，x=9.‎ 即当容器内的水量大于5升时，时间x的取值范围是1＜x＜9.‎