八年级下数学课件《用待定系数法确定一次函数表达式和性质》课件1_冀教版 12页

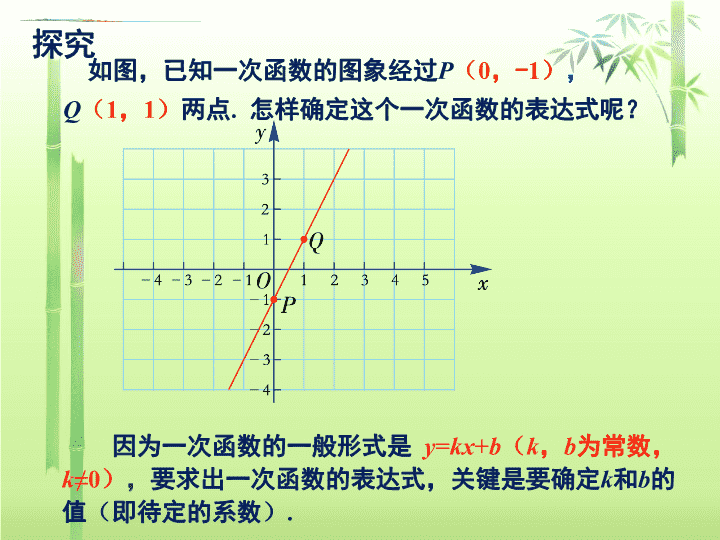
如图，已知一次函数的图象经过P（0，-1）， Q（1，1）两点. 怎样确定这个一次函数的表达式呢？ 探究 因为一次函数的一般形式是 y=kx+b（k，b为常数， k≠0），要求出一次函数的表达式，关键是要确定k和b 的值（即待定的系数）. 因为P（0，-1） 和Q（1，1）都在该函数图象上， 因 此它们的坐标应满足y=kx+b ， 将这两点坐标代入该式中， 得到一个关于k，b的二元一次方程组： k·0 + b = -1， k + b = 1. ｛ ｛解得 k=2， b=-1. 所以，这个一次函数的表达式为y = 2x- 1. 像这样，通过先设定函数表达式（确定函数模型）， 再根据条件确定表达式中的未知系数，从而求出函数 的表达式的方法，称为待定系数法. 例 一辆汽车匀速行驶，当行驶了20km时，油箱剩余 58.4L油；当行驶了50km时，油箱剩余56L油．如果油 箱中剩余油量y（L）与汽车行驶的路程x（km）之间 是一次函数关系，请求出这个一次函数的表达式，并 写出自变量x的取值范围以及常数项的意义． 解：设所求一次函数的表达式为y=kx+b．根据题意， 把已知的两组对应值（20，58.4）和（50，56）代入 y=kx+b，得 解得      .5056 204.58 bk bk ，      .60 08.0 b k ，- 这个一次函数表达式为y=-0.08x+60. 因为剩余油量y≥0，所以-0.08x+60≥0.解得x≤750. 因为路程x≥0，所以0≤x≤750. 因为当x=0时，y=60，所以这辆汽车行驶前油箱存油 60L. 如果知道一个一次函数，当自变量x=4时函数 值y=5；当x=5时，y=2.写出函数表达式并画出 它的图象. 解 因为y是x的一次函数，设其表达式为y=kx+b 由题可得： 4k+b=5 5k+b=2 解方程组，得：k=-3，b=17，所以函数 表达式为：y=-3x+17 函数图像如下图： 用待定系数法确定一次函数表达式的一般步骤 函数解 析 y=kx+b 满足条 件的两 定点(x1， y1)与(x2， y2) 一次 函数 的图 象 选取 解出 画出 选取 归 纳 1、设——设函数表达式为y=kx+b 2、代——将点的坐标代入y=kx+b中， 列出关于k、b的方程（或方程组） 3、求——解方程（或方程组），求k、b 4、写——把求出的k、b的值代回到表达 式中即可. 练习：已知一次函数的图象经过点(3，5)与 （－4，－9）.求这个一次函数的表达式． 解：设这个一次函数的表达式为y=kx+b. ∵y=kx+b的图象过点（3，5）与（-4，-9）. ∴ 3k+b=5 -4k+b=-9 解得 k=2 b=-1 ∴这个一次函数的表达式为y=2x-1 变式训练：已知一次函数y=kx+b，当x=1 时，y=1；当x=2时，y=3.求这个一次函数 的表达式． 解： ∴ k+b=1 2k+b=3 解得 k=2 b=-1 ∴这个一次函数的表达式为y=2x-1 ∵当x=1时，y=1；当x=2时，y=3. 训练：小明根据某个一次函数关系式填写 了下表: x -1 0 1 y 2 4 其中有一格不慎被墨汁遮住了，想想看， 该空格里原来填的数是多少？解释你的理 由. ∴ b=2 k+b=4 ∴y=2x+2∴x=-1时y=0 ∵当x=0时，y=1，当x=1时，y=0. ∴ k=2 b=2 解：设这个一次函数的解析式为y=kx+b. 某车油箱现有汽油50升，行驶时，油箱中的余油量y（升） 是行驶路程x（km）的一次函数，其图象如图所示求y与x 的函数关系式，并写出自变量x的取值范围. 60 50 30 ０ x/km y/升 解：设函数解析式为y = kx＋b，且图象过点（60，30） 和点（0，50），所以 k60  b 30 0  b 50 ① ② 解得 3 1k 50b 的函数关系式为与xy 503 1  xy  1500  x