2020八年级数学上册第1章三角形的初步知识1 4页

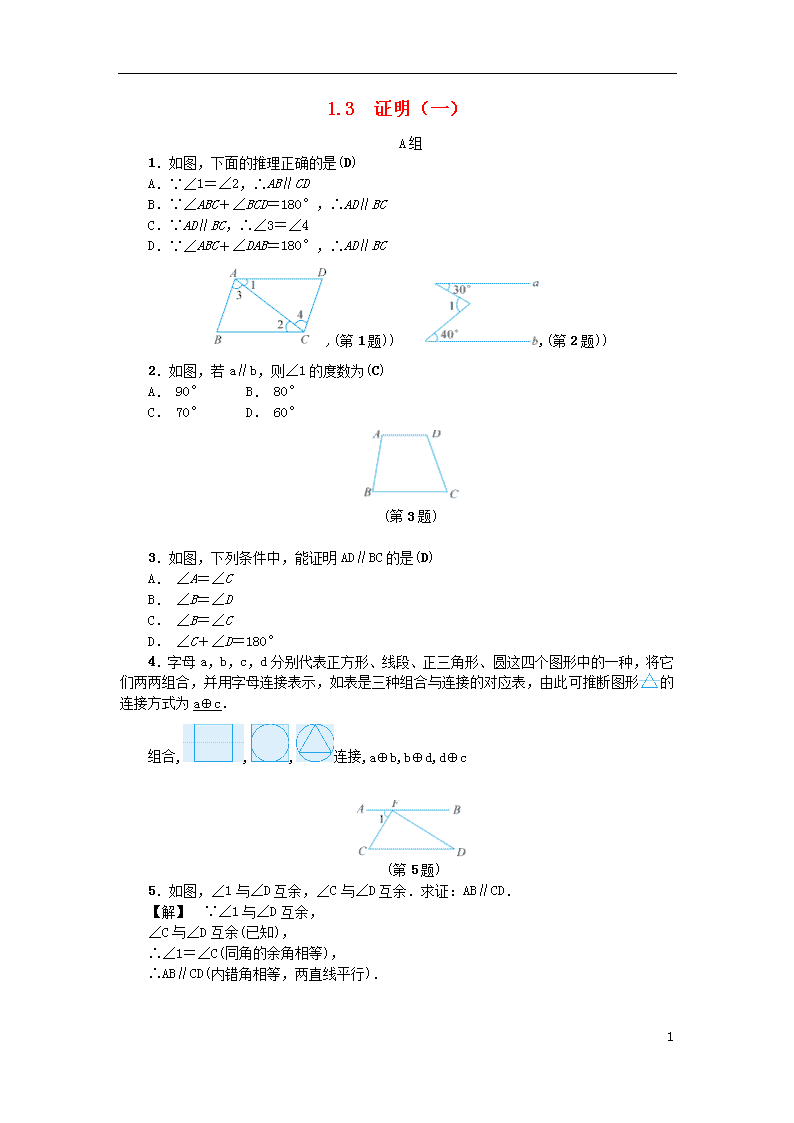
‎1.3 证明（一）‎ A组 ‎1．如图，下面的推理正确的是(D)‎ A．∵∠1＝∠2，∴AB∥CD B．∵∠ABC＋∠BCD＝180°，∴AD∥BC C．∵AD∥BC，∴∠3＝∠4‎ D．∵∠ABC＋∠DAB＝180°，∴AD∥BC ‎,(第1题))　　,(第2题))‎ ‎2．如图，若a∥b，则∠1的度数为(C)‎ A． 90°　　 B． 80°　　‎ C． 70°　　 D． 60°‎ ‎(第3题)‎ ‎3．如图，下列条件中，能证明AD∥BC的是(D)‎ A． ∠A＝∠C B． ∠B＝∠D C． ∠B＝∠C D． ∠C＋∠D＝180°‎ ‎4．字母a，b，c，d分别代表正方形、线段、正三角形、圆这四个图形中的一种，将它们两两组合，并用字母连接表示，如表是三种组合与连接的对应表，由此可推断图形的连接方式为a⊕c．‎ 组合,,,连接,a⊕b,b⊕d,d⊕c ‎ (第5题)‎ ‎5．如图，∠1与∠D互余，∠C与∠D互余．求证：AB∥CD．‎ ‎【解】　∵∠1与∠D互余，‎ ‎∠C与∠D互余(已知)，‎ ‎∴∠1＝∠C(同角的余角相等)，‎ ‎∴AB∥CD(内错角相等，两直线平行)．‎ 4‎ ‎(第6题)‎ ‎6．如图，直线a∥b，三角形纸板的直角顶点A落在直线a上，两条直线分别交直线b于B，C两点．若∠1＝42°，求∠2的度数．‎ ‎【解】　∵直线a∥b，∠1＝42°(已知)，‎ ‎∴∠ACB＝42°(两直线平行，内错角相等)．‎ 又∵∠BAC＝90°(已知)，‎ ‎∴∠ABC＝180°－∠BAC－∠ACB＝48°(三角形的内角和为180°)，‎ ‎∴∠2＝∠ABC＝48°(对顶角相等)．‎ ‎(第7题)‎ ‎7．如图，∠1＝∠2，∠D＝50°，求∠B的度数．‎ ‎【解】　∵∠1＝∠AGF(对顶角相等)，‎ ‎∠1＝∠2(已知)，‎ ‎∴∠2＝∠AGF(等量代换)，‎ ‎∴AB∥CD(同位角相等，两直线平行)，‎ ‎∴∠B＋∠D＝180°(两直线平行，同旁内角互补)，‎ ‎∴∠B＝180°－∠D＝180°－50°＝130°．‎ B组 ‎(第8题)‎ ‎8．如图，已知直线a∥b，直角三角形ABC的顶点B在直线a上，∠C＝90°，∠β＝55°，则∠α的度数为__35°__．‎ ‎【解】　过点C作CE∥a．‎ ‎∵a∥b，∴CE∥a∥b，‎ ‎∴∠BCE＝∠α，∠ACE＝∠β＝55°．‎ ‎∵∠ACB＝90°，‎ ‎∴∠α＝∠BCE＝∠ACB－∠ACE＝35°．‎ 4‎ ‎(第9题)‎ ‎9．如图，已知AB∥CD，EF与AB，CD分别相交于点E，F，EP⊥EF，与∠EFD的平分线FP相交于点P，且∠BEP＝50°，则∠EPF的度数为__70°__．‎ ‎【解】　∵EP⊥EF，∴∠PEF＝90°．‎ 又∵∠BEP＝50°，‎ ‎∴∠BEF＝∠BEP＋∠PEF＝140°．‎ ‎∵AB∥CD，∴∠BEF＋∠EFD＝180°，‎ ‎∴∠EFD＝40°．‎ ‎∵FP平分∠EFD，‎ ‎∴∠EFP＝∠EFD＝20°．‎ ‎∵∠PEF＋∠EFP＋∠EPF＝180°，‎ ‎∴∠EPF＝70°．‎ ‎10．如图，在△ABC中，∠ACB＝90°，CD⊥AB，BE平分∠ABC，分别交AC，CD于点E，F．求证：∠CEF＝∠CFE．‎ ‎(第10题)‎ ‎【解】　∵BE平分∠ABC，‎ ‎∴∠ABE＝∠CBE．‎ ‎∵∠ACB＝90°，CD⊥AB，‎ ‎∴∠CEF＋∠CBE＝90°，∠DFB＋∠ABE＝90°，‎ ‎∴∠CEF＝∠DFB．‎ 又∵∠CFE＝∠DFB，‎ ‎∴∠CEF＝∠CFE．‎ ‎11．阅读：如图①，∵CE∥AB，∴∠1＝∠A，∠2＝∠B，∴∠ACD＝∠1＋∠2＝∠A＋∠B．这是一个有用的事实，请用这个事实，在图②中的四边形ABCD内引一条和边平行的直线，求出∠A＋∠B＋∠C＋∠D的度数．‎ ‎ (第11题)‎ 4‎ ‎ (第11题解)‎ ‎【解】　如解图，过点D作DE∥AB交BC于点E，则∠A＋∠ADE＝180°，∠B＋∠BED＝180°．‎ 由题意，得∠BED＝∠C＋∠CDE，‎ ‎∴∠A＋∠B＋∠C＋∠CDA＝(∠A＋∠ADE)＋(∠CDE＋∠C)＋∠B＝180°＋∠BED＋∠B＝180°＋180°＝360°．‎ 数学乐园 ‎12．如图，∠EOF＝90°，点A，B分别在射线OE，OF上移动，连结AB并延长至点D，∠DBO的平分线与∠OAB的平分线交于点C，试问：∠ACB的度数是否随点A，B的移动而发生变化？如果保持不变，请说明理由；如果随点A，B的移动而发生变化，请给出变化的范围．‎ ‎(第12题)‎ ‎【解】　∠ACB的度数不随点A，B的移动发生变化．理由如下：‎ ‎∵BC，AC分别平分∠DBO，∠BAO，‎ ‎∴∠DBC＝∠DBO，‎ ‎∠BAC＝∠BAO．‎ ‎∵∠DBO＋∠OBA＝180°，∠OBA＋∠BAO＋∠AOB＝180°，‎ ‎∴∠DBO＝∠BAO＋∠AOB，‎ ‎∴∠DBO－∠BAO＝∠AOB＝90°．‎ ‎∵∠DBC＋∠ABC＝180°，∠ABC＋∠ACB＋∠BAC＝180°，‎ ‎∴∠DBC＝∠BAC＋∠ACB，‎ ‎∴∠DBO＝∠BAO＋∠ACB，‎ ‎∴∠ACB＝(∠DBO－∠BAO)＝∠AOB＝45°．‎ 4‎