2020八年级数学上册 第14章 整式的乘法与因式分解 14 8页

1 完全平方公式 【学习目标】 1．完全平方公式的推导及其应用；完全平方公式的几何解释． 2．经历探索完全平方公式的过程，进一步发展符号感和推理能力． 【学习重点】完全平方公式的推导过程、结构特点、几何解释，灵活应用． 【学习难点】 理解完全平方公式的结构特征并能灵活应用公式进行计算． 【学习过程】 一、知识链接： 1、叙述平方差公式的内容及用字母表示： , . 2、用简便方法计算： （1）103 （2）998 3、请同学们自编一个符合平方差公式结构的计算题，并算出结果。 二、自主学习：阅读 P109—110 1、计算下列各式，你能发现什么规律？ （1）（p+1）2=（p+1）（p+1）= ； （2）（m+2）2=___ ； 97× 1002× 2 （3）（p-1）2=（p-1）（p-1）= ； （4）（m-2）2= ； （5）（a+b）2= ； （6）（a -b）2= ． 把你发现的规律用文字叙述为： . 符号叙述： . 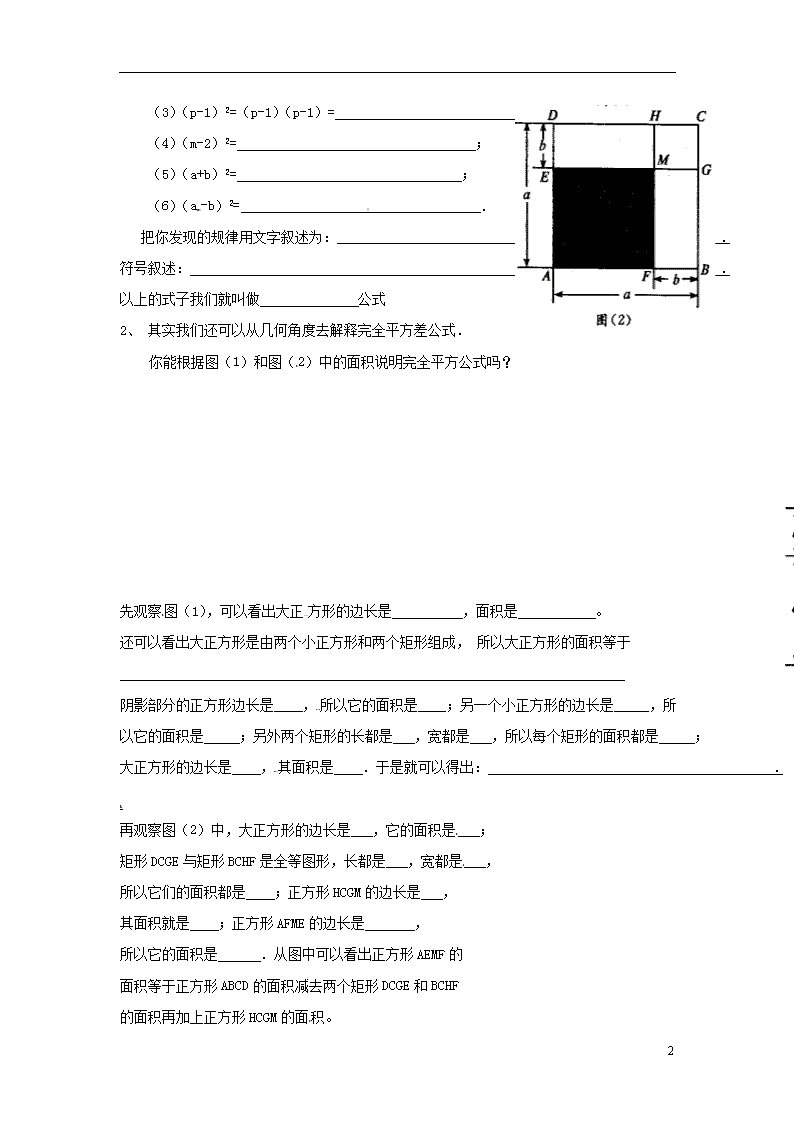以上的式子我们就叫做 公式 2、 其实我们还可以从几何角度去解释完全平方差公式． 你能根据图（1）和图（ 2）中的面积说明完全平方公式吗？ 先观察 图（1），可以看出大正方形的边长是 ，面积是 。 还可以看出大正方形是由两个小正方形和两个矩形组成，所以大正方形的面积等于 阴影部分的正方形边长是 ， 所以它的面积是 ；另一个小正方形的边长是 ，所 以它的面积是 ；另外两个矩形的长都是 ，宽都是 ，所以每个矩形的面积都是 ； 大正方形的边长是 ， 其面积是 ．于是就可以得出： . 再观察图（2）中，大正方形的边长是 ，它的面积是 ； 矩形 DCGE 与矩形 BCHF 是全等图形，长都是 ，宽都是 ， 所以它们的面积都是 ；正方形 HCGM 的边长是 ， 其面积就是 ；正方形 AFME 的边长是 ， 所以它的面积是 ．从图中可以看出正方形 AEMF 的 面积等于正方形 ABCD 的面积减去两个矩形 DCGE 和 BCHF 的面积再加上正方形 HCGM 的面 积。 3 也就是： ．这也正好符合完全平方公式． 三、学以致用 1、应用完全平方公式计算： （1）（4m+n）2 （2）（y- ）2 （3）（-a-b）2 （4）（b-a）2 2、运用完全平方公式计算： （1）1022 （2）992 四、课堂巩固： 1、运用完全平方公式计算： （1） （2） （3） （4） 1 2 ( )6 2+x ( )5 2−y ( )52 2+− x    − yx 3 2 4 3 2 4 2、下面各式的计算错在哪里？应当怎样改正？ （1） （2） 五、课堂小结：完全平方公式符号叙述为： . 文字叙述为： . 六、课后反思： , . （实际用 课时） 八年级（上）数 学 讲学稿 课题： 14.2.1 完全平方公式 （2） 课型：新课 计划课时： 1 【学习目标】 1、掌握添括号法则的推导，会综合运用添括号法则、平方差公式、完全平方公式解决问题。 2、经历添括号法则的探究，学习逆向思维，经历合作交流，学习根据数学式子的结构特点， 适当恒等变形和灵活运用公式 【学习重点】 添括号法则的推导，知识的综合运用 【学习难点】 添括号在具体问题中的灵活应用 【学习过程】 一、知识链接： 1、填空：（1）平方差公式（a+b）(a-b)= . ( ) baba 222 +=+ ( ) baba 222 −=− 5 (2)完全平方公式 = . (3)去括号法则： , . 2、运用平方差公式计算： （1） （2） （3） 3、运用完全平方公式计算： （1） （2） （3） 二、探究添括号法则：阅读 P111—112. 有一些多项式乘多项式，例如： 和 ，没有办法直接运 用公式，这时候，我们需要把一个多项式看作一个整体，把另外一个多项式看作另外一个整 体，这就需要在式子里添加括号。那么如何加括号呢？它有什么法则呢？ 1、去括号： ( ) =+ba 2 ( )ba− 2      +     − yxyx 3 2 3 2 ( )( )11 −+ xyxy ( )( )5252 −−− bb ( )32 2−−yx ( )( )11 −+++ yxyx ( )( )[ ]22 2−+ xx ))(( cbacba +−++ 2)( cba ++ 6 = . = . 2、添括号： ( ) ( ) ( ) ( ) 3、归纳添括号法则： 添括号时，如果括号前面是 ，括到括号里的各项 ； 如 果 括 号 前 面 是 ， 括 到 括 号 里 的 各 项 . 4、试一试 判断下列 运算是否正确，不正确的请改正。 （ 1 ） （ 2 ） （3） （4） 三、例题应用 例 1.运用乘法公式计算： （1） （2）  （3） （4） )( cba ++ =−+ )( cba =+− )( cba )( cba −− +=++ acba +=−+ acba −=−− acba −=+− acba )2(222 cbacba −−=−− )23(23 banmbanm −++=−+− )232(232 −+−=+− yyyy )54()2(542 +−−=+−− cbacba )32)(32( +−−+ yxyx ))(( cbacba +−++ 2)( cba ++ )2)(2( cbacba −+−− 7  四、课堂检测 1、运用乘法公式计算： （1） （2）  （3） （4） 2、计算：（1） （2）  五、能力提高: 1、计算： 2、如果 ，求 的值。 2)12( −+ ba )2)(2( zyxzyx −−++ )1)(1( −+++ yxyx 2)32( −− yx 22 )72()53( +−− xx [ ]2)2)(2( −+ xx )2()( 222 bababa +−+ 422 =− yx 22 )()( yxyx +− 8 3、如图，一块直径为 a+b 的圆形钢板，从中挖去直径为 a 与 b 的两个圆，求剩下的钢板的 面积。 五、课后 反思： ,