八年级数学上册第二章实数小结与复习教学课件新版北师大版 19页

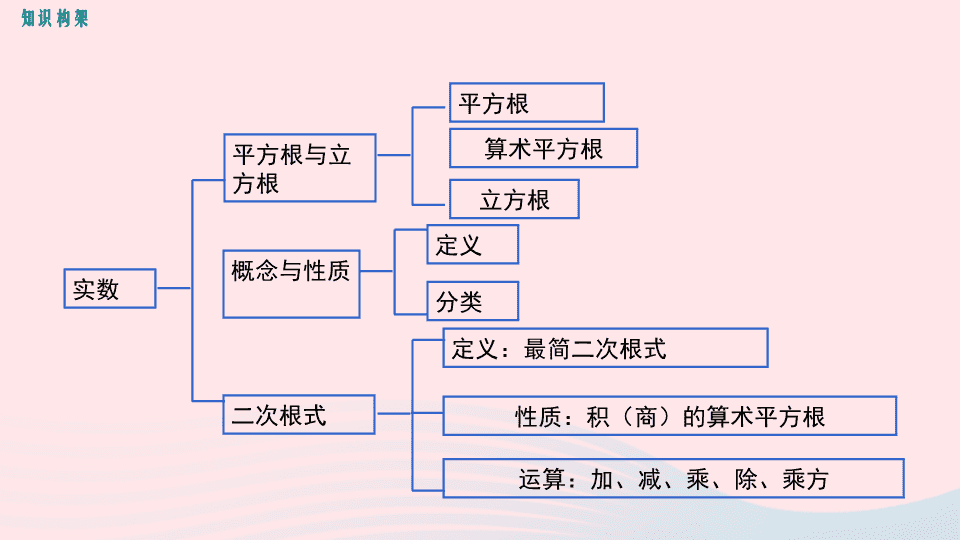
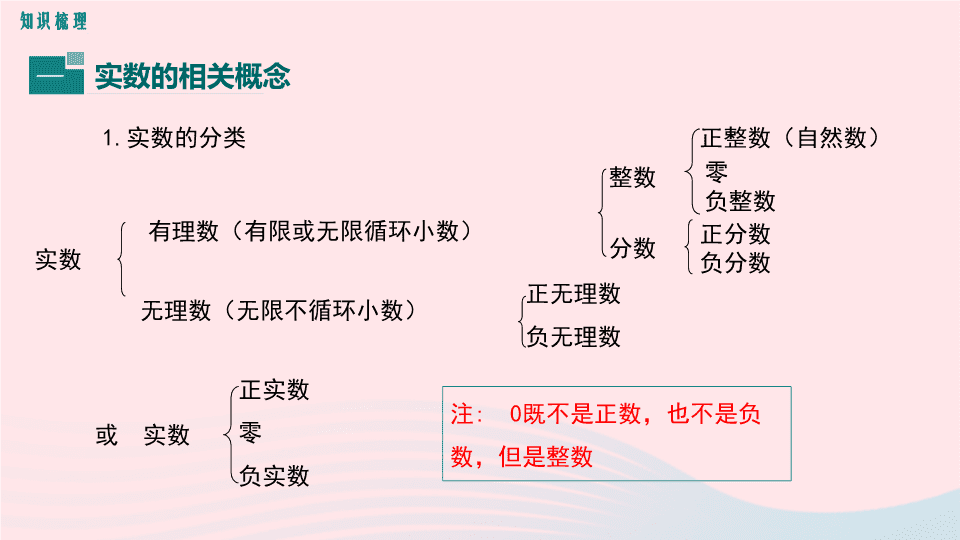
小结 与 复习 第二章 实数 八年级数学 · 北师版 平方根与立方根 二次根式 实数 平方根 算术平方根 定义：最简二次根式 性质：积（商）的算术平方根 运算：加、减、乘、除、乘方 立方根 概念与性质 定义 分类 知识构架 实数的相关概念 一 实数 有理数（有限或无限循环小数） 整数 分数 正整数（自然数） 零 负整数 正分数 负分数 无理数（无限不循环小数） 正无理数 负无理数 或 实数 正实数 零 负实数 注 : 0 既不是正数，也不是负数，但是整数 1. 实数的分类 知识梳理 2. 数轴 ①三要素 : 原点、单位长度、正方向 ②与实数一一对应 3. 相反数、倒数 a 与 - a 相反数的两数和为 0 （ a 与 b 互为相反数 a + b =0 ） b 与 倒数的两数积为 1 （ a 与 b 互为倒数 ab =1 ） 4. 绝对值（到原点的距离） ① | a |= a （ a >0) 0 （ a =0 ） - a （ a <0 ） | a | 为非负数，即 | a |≥0 ②非负数形式有 ： | a | ； a 2 ； ； 5. 实数的大小比较 ①利用数轴（右边的数总比左边大） ②作差与 0 比 ③作商与 1 比 平方根与立方根 二 算术平方根的意义： （ a ≥0 ） 算术平方根具有 双重非负性 非负数 ≥ 0 正数 a 的正的平方根，叫做这个正数的 算术平方根 0 的算术平方根是 0 ，即 平方根的定义： 若 ，则 x 叫 a 的平方根 , 即 类比 当 ，则 x 叫做什么呢？ x 叫 a 的立方根 即： 开平方的定义 类比 开立方的定义 平方根的性质 立方根的性质 求一个数 a 的立方根的运算，叫做开立方，其中 a 叫做被开方数 如：求 8 的立方根 一个正数有两个平方根； 0 只有一个平方根，它是 0 本身； 负数没有平方根 . 正数的立方根是正数； 负数的立方根是负数； 0 的立方根是 0. 求一个数 a 的平方根的运算，叫做开平方，其中 a 叫做被开方数 如：求 9 的平方根 二次根式 三 1 、定义： 形如 　　　　　 的式子叫做二次根式， 2 、性质： ⑴积的算术平方根： 等于算术平方根的积； ⑵商的算术平方根： 等于算术平方根的商； 其中 a 叫做被开方数 . 3 、最简二次根式 ： 满足以下 三个 条件的二次根式叫 最简 二次根式 ： ⑴被开方数不能含有开得尽方的因数或因式； ⑵被开方数不能含有分母； ⑶分母不能含有根号 . 注意： 二次根式的化简与运算，最后结果应化成最简二次根式 . 4 、二次根式的运算 ： ⑴二次根式的加减： 类似合并同类项 ； ⑵二次根式的乘法 ： ⑶二次根式的除法 ： (4) 二次根式的乘方 ： 注意 : 平方差公式与完全平方公式的运用！ 中无理数的个数是（ ） A. 2 B. 3 C. 4 D. 5 A 1. 下列各数 2. 一个长方形的长与宽分别是 6 、 3 ，它的对角线的长可 能是（ ） A. 整数 D. 无理数 C. 有理数 B. 分数 D 当堂练习 3. 下列语句中正确的是（ ） A. -9 的平方根是 -3 B. 9 的平方根是 3 C. 9 的算术平方根是 D. 9 的算术平方根是 3 D 4. 下列运算中，正确的是（ ） A 5. 的平方根是（ ） A. C. 5 B. -5 D. 6. 下列运算正确的是 ( ) D D 7. 已知一个正方形的边长为 面积为 , 则 ( ) C 8.9 的算术平方根是 ; 9.(-5) 3 的立方根是 ; 10.10 -2 的平方根是 ; 3 -5 ±0.1 11. 比较大小： 与 解：∵ (-2+ )-(-2+ )=-2+ +2- = - ＞ 0, ∴ -2+ ＞ -2+ 另解：直接由正负决定 -2+ ＞ -2+ 12. 实数 a,b,c,d 在数轴上的对应点如图所示，则 它们从小到大的顺序是 . c d 0 b a 其中： c