2020年四川省遂宁市中考数学试卷【含答案】 11页

1 / 11 2020 年四川省遂宁市中考数学试卷 一、选择题（本大题共 10 个小题，每小题 4 分，共 40 分，在每个小题给出的四个选 项中，只有一个符合题目要求．） 1.−5的相反数是() A.5 B.−5 C.1 5 D.− 1 5 2.已知某新型感冒病毒直径约为0.000000823米，将0.000000823用科学记数法表示() A.8.23 × 10−6 B.8.23 × 10−7 C.8.23 × 106 D.8.23 × 107 3.下列计算正确的是（） A.7푎푏 − 5푎＝2푏 B.(푎 + 1 푎)2＝푎2 + 1 푎2 C.(−3푎2푏)2＝6푎4푏2 D.3푎2푏 ÷ 푏＝3푎2 4.下列图形中，既是轴对称图形，又是中心对称图形的是（） A.等边三角形 B.平行四边形 C.矩形 D.正五边形 5.函数푦 = √푥+2 푥−1 中，自变量푥的取值范围是（） A.푥 > −2 B.푥 ≥ −2 C.푥 > −2且푥 ≠ 1 D.푥 ≥ −2且푥 ≠ 1 6.关于푥的分式方程 푚 푥−2 − 3 2−푥 = 1有增根，则푚的值（） A.푚＝2 B.푚＝1 C.푚＝3 D.푚＝−3 7.如图，在平行四边形퐴퐵퐶퐷中，∠퐴퐵퐶的平分线交퐴퐶于点퐸，交퐴퐷于点퐹，交퐶퐷的 延长线于点퐺，若퐴퐹＝2퐹퐷，则퐵퐸 퐸퐺 的值为（） A.1 2 B.1 3 C.2 3 D.3 4 8.二次函数푦＝푎푥2 + 푏푥 + 푐(푎 ≠ 0)的图象如图所示，对称轴为直线푥＝−1，下列结论 不正确的是（） A.푏2 > 4푎푐 B.푎푏푐 > 0 C.푎 − 푐 < 0 D.푎푚2 + 푏푚 ≥ 푎 − 푏（푚为任意实数） 9.如图，在푅푡 △ 퐴퐵퐶中，∠퐶＝90∘，퐴퐶＝퐵퐶，点푂在퐴퐵上，经过点퐴的⊙ 푂与퐵퐶相 切于点퐷，交퐴퐵于点퐸，若퐶퐷 = √2，则图中阴影部分面积为（） A.4 − 휋 2 B.2 − 휋 2 C.2 − 휋 D.1 − 휋 4 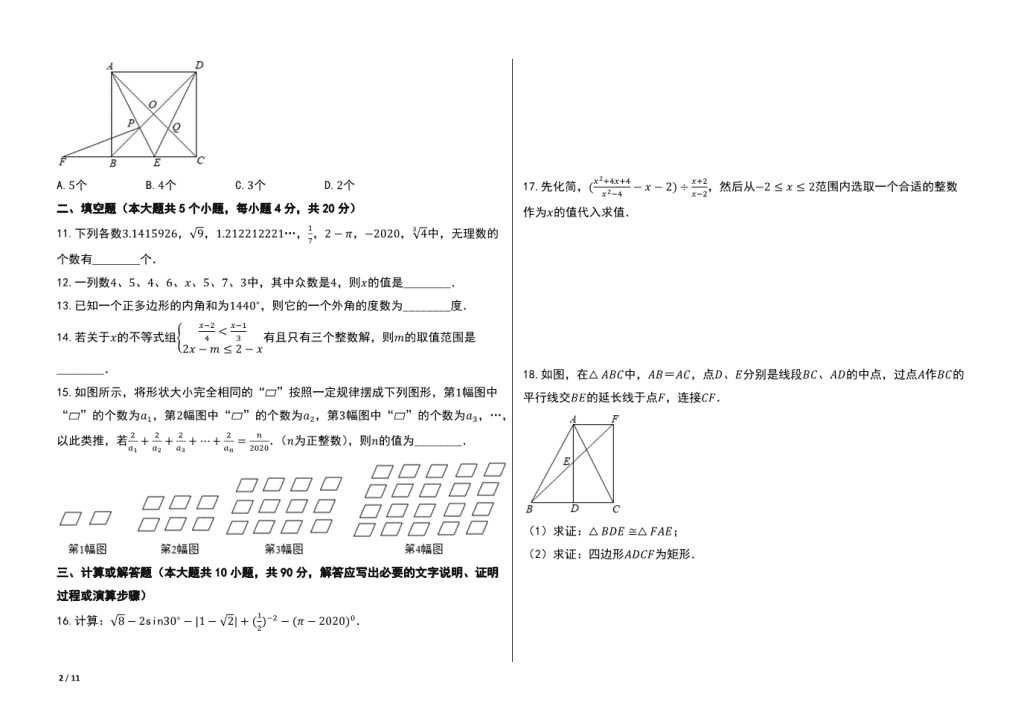10.如图，在正方形퐴퐵퐶퐷中，点퐸是边퐵퐶的中点，连接퐴퐸、퐷퐸，分别交퐵퐷、퐴퐶于点 푃、푄，过点푃作푃퐹 ⊥ 퐴퐸交퐶퐵的延长线于퐹，下列结论： ①∠퐴퐸퐷 + ∠퐸퐴퐶 + ∠퐸퐷퐵＝90∘， ②퐴푃＝퐹푃， ③퐴퐸 = √10 2 퐴푂， ④若四边形푂푃퐸푄的面积为4，则该正方形퐴퐵퐶퐷的面积为36， ⑤퐶퐸 ⋅ 퐸퐹＝퐸푄 ⋅ 퐷퐸． 其中正确的结论有（） 2 / 11 A.5个 B.4个 C.3个 D.2个 二、填空题（本大题共 5 个小题，每小题 4 分，共 20 分） 11.下列各数3.1415926，√9，1.212212221…，1 7 ，2 − 휋，−2020，√43 中，无理数的 个数有________个． 12.一列数4、5、4、6、푥、5、7、3中，其中众数是4，则푥的值是________． 13.已知一个正多边形的内角和为1440∘，则它的一个外角的度数为________度． 14.若关于푥的不等式组{ 푥−2 4 < 푥−1 3 2푥 − 푚 ≤ 2 − 푥 有且只有三个整数解，则푚的取值范围是 ________． 15.如图所示，将形状大小完全相同的“▱”按照一定规律摆成下列图形，第1幅图中 “▱”的个数为푎1，第2幅图中“▱”的个数为푎2，第3幅图中“▱”的个数为푎3，…， 以此类推，若 2 푎1 + 2 푎2 + 2 푎3 + ⋯ + 2 푎푛 = 푛 2020 ．（ 푛为正整数），则푛的值为________． 三、计算或解答题（本大题共 10 小题，共 90 分，解答应写出必要的文字说明、证明 过程或演算步骤） 16.计算：√8 − 2sin30∘ − |1 − √2| + (1 2)−2 − (휋 − 2020)0． 17.先化简，(푥2+4푥+4 푥2−4 − 푥 − 2) ÷ 푥+2 푥−2 ，然后从−2 ≤ 푥 ≤ 2范围内选取一个合适的整数 作为푥的值代入求值． 18.如图，在△ 퐴퐵퐶中，퐴퐵＝퐴퐶，点퐷、퐸分别是线段퐵퐶、퐴퐷的中点，过点퐴作퐵퐶的 平行线交퐵퐸的延长线于点퐹，连接퐶퐹． （1）求证：△ 퐵퐷퐸 ≅△ 퐹퐴퐸； （2）求证：四边形퐴퐷퐶퐹为矩形． 3 / 11 19.在数学实践与综合课上，某兴趣小组同学用航拍无人机对某居民小区的1、2号楼 进行测高实践，如图为实践时绘制的截面图．无人机从地面点퐵垂直起飞到达点퐴处， 测得1号楼顶部퐸的俯角为67∘，测得2号楼顶部퐹的俯角为40∘，此时航拍无人机的高度 为60米，已知1号楼的高度为20米，且퐸퐶和퐹퐷分别垂直地面于点퐶和퐷，点퐵为퐶퐷的 中点，求2号楼的高度．（结果精确到0.1） （参考数据sin40∘ ≈ 0.64，cos40∘ ≈ 0.77，tan40∘ ≈ 0.84，sin67∘ ≈ 0.92， cos67∘ ≈ 0.39，tan67∘ ≈ 2.36） 20.新学期开始时，某校九年级一班的同学为了增添教室绿色文化，打造温馨舒适的 学习环境，准备到一家植物种植基地购买퐴、퐵两种花苗．据了解，购买퐴种花苗3盆， 퐵种花苗5盆，则需210元；购买퐴种花苗4盆，퐵种花苗10盆，则需380元． （1）求퐴、퐵两种花苗的单价分别是多少元？ （2）经九年级一班班委会商定，决定购买퐴、퐵两种花苗共12盆进行搭配装扮教 室．种植基地销售人员为了支持本次活动，为该班同学提供以下优惠：购买几盆퐵种 花苗，퐵种花苗每盆就降价几元，请你为九年级一班的同学预算一下，本次购买至少 准备多少钱？最多准备多少钱？ 21.阅读以下材料，并解决相应问题： 小明在课外学习时遇到这样一个问题： 定义：如果二次函数푦＝푎1푥2 + 푏1푥 + 푐1（푎1 ≠ 0，푎1、푏1、푐1是常数）与푦＝푎2푥2 + 푏2푥 + 푐2（푎2 ≠ 0，푎2、푏2、푐2是常数）满足푎1 + 푎2＝0，푏1＝푏2，푐1 + 푐2＝0，则这 两个函数互为“旋转函数”．求函数푦＝2푥2 − 3푥 + 1的旋转函数，小明是这样思考的， 由函数푦＝2푥2 − 3푥 + 1可知，푎1＝2，푏1＝−3，푐1＝1，根据푎1 + 푎2＝0，푏1＝푏2， 푐1 + 푐2＝0，求出푎2，푏2，푐2就能确定这个函数的旋转函数． 请思考小明的方法解决下面问题： （1）写出函数푦＝푥2 − 4푥 + 3的旋转函数． 4 / 11 （2）若函数푦＝5푥2 + (푚 − 1)푥 + 푛与푦＝−5푥2 − 푛푥 − 3互为旋转函数，求(푚 + 푛)2020的值． （3）已知函数푦＝2(푥 − 1)(푥 + 3)的图象与푥轴交于퐴、퐵两点，与푦轴交于点퐶，点퐴、 퐵、퐶关于原点的对称点分别是퐴1、퐵1、퐶1，试求证：经过点퐴1、퐵1、퐶1的二次函数 与푦＝2(푥 − 1)(푥 + 3)互为“旋转函数”． 22.端午节是中国的传统节日．今年端午节前夕，遂宁市某食品厂抽样调查了河东某 居民区市民对퐴、퐵、퐶、퐷四种不同口味粽子样品的喜爱情况，并将调查情况绘制成 如图两幅不完整统计图： （1）本次参加抽样调查的居民有________人． （2）喜欢퐶种口味粽子的人数所占圆心角为________度．根据题中信息补全条形统计 图． （3）若该居民小区有6000人，请你估计爱吃퐷种粽子的有________人． （4）若有外型完全相同的퐴、퐵、퐶、퐷棕子各一个，煮熟后，小李吃了两个，请用列 表或画树状图的方法求他第二个吃的粽子恰好是퐴种粽子的概率． 5 / 11 23.如图，在平面直角坐标系中，已知点퐴的坐标为(0,  2)，点퐵的坐标为(1,  0)，连结 퐴퐵，以퐴퐵为边在第一象限内作正方形퐴퐵퐶퐷，直线퐵퐷交双曲线푦 = 푘 푥 (푘 ≠ 0)于퐷、퐸 两点，连结퐶퐸，交푥轴于点퐹． （1）求双曲线푦 = 푘 푥 (푘 ≠ 0)和直线퐷퐸的解析式． （2）求△ 퐷퐸퐶的面积． 24.如图，在푅푡 △ 퐴퐵퐶中，∠퐴퐶퐵＝90∘，퐷为퐴퐵边上的一点，以퐴퐷为直径的⊙ 푂交 퐵퐶于点퐸，交퐴퐶于点퐹，过点퐶作퐶퐺 ⊥ 퐴퐵交퐴퐵于点퐺，交퐴퐸于点퐻，过点퐸的弦퐸푃交 퐴퐵于点푄（퐸푃不是直径），点푄为弦퐸푃的中点，连结퐵푃，퐵푃恰好为⊙ 푂的切线． （1）求证：퐵퐶是⊙ 푂的切线． （2）求证：퐸퐹̂ = 퐸퐷̂ ． （3）若sin∠퐴퐵퐶 = 3 5 ，퐴퐶＝15，求四边形퐶퐻푄퐸的面积． 6 / 11 25.如图，抛物线푦＝푎푥2 + 푏푥 + 푐(푎 ≠ 0)的图象经过퐴(1,  0)，퐵(3,  0)，퐶(0,  6)三点． （1）求抛物线的解析式． （2）抛物线的顶点푀与对称轴푙上的点푁关于푥轴对称，直线퐴푁交抛物线于点퐷，直线 퐵퐸交퐴퐷于点퐸，若直线퐵퐸将△ 퐴퐵퐷的面积分为1: 2两部分，求点퐸的坐标． （3）푃为抛物线上的一动点，푄为对称轴上动点，抛物线上是否存在一点푃，使퐴、퐷、 푃、푄为顶点的四边形为平行四边形？若存在，求出点푃的坐标；若不存在，请说明理 由． 7 / 11 参考答案与试题解析 2020 年四川省遂宁市中考数学试卷 一、选择题（本大题共 10 个小题，每小题 4 分，共 40 分，在每个小题给出的四个选 项中，只有一个符合题目要求．） 1.A 2.B 3.D 4.C 5.D 6.D 7.C 8.C 9.B 10.B 二、填空题（本大题共 5 个小题，每小题 4 分，共 20 分） 11.3 12.4 13.36 14.1 < 푚 ≤ 4 15.4039 三、计算或解答题（本大题共 10 小题，共 90 分，解答应写出必要的文字说明、证明 过程或演算步骤） 16.原式＝2√2 − 2 × 1 2 − (√2 − 1) + 4 − 1 ＝2√2 − 1 − √2 + 1 + 4 − 1 = √2 + 3． 17.原式＝[ (푥+2)2 (푥+2)(푥−2) − (푥 + 2)]•푥−2 푥+2 ＝(푥+2 푥−2 − 푥2−4 푥−2 ) ⋅ 푥−2 푥+2 = −푥2 + 푥 + 6 푥 − 2 ⋅ 푥 − 2 푥 + 2 = − (푥 + 2)(푥 − 3) 푥 − 2 ⋅ 푥 − 2 푥 + 2 ＝−(푥 − 3) ＝−푥 + 3， ∵푥 ≠ ±2， ∴可取푥＝1， 则原式＝−1 + 3＝2． 18.∵퐴퐹 // 퐵퐶， ∴∠퐴퐹퐸＝∠퐷퐵퐸， ∵퐸是线段퐴퐷的中点， ∴퐴퐸＝퐷퐸， ∵∠퐴퐸퐹＝∠퐷퐸퐵， ∴△ 퐵퐷퐸 ≅△ 퐹퐴퐸(퐴퐴푆)； ∵△ 퐵퐷퐸 ≅△ 퐹퐴퐸， ∴퐴퐹＝퐵퐷， ∵퐷是线段퐵퐶的中点， ∴퐵퐷＝퐶퐷， ∴퐴퐹＝퐶퐷， ∵퐴퐹 // 퐶퐷， ∴四边形퐴퐷퐶퐹是平行四边形， ∵퐴퐵＝퐴퐶， ∴퐴퐷 ⊥ 퐵퐶， ∴∠퐴퐷퐶＝90∘， ∴四边形퐴퐷퐶퐹为矩形． 19.2号楼的高度约为45.8米． 20.设퐴、퐵两种花苗的单价分别是푥元和푦元，则{ 3푥 + 5푦 = 210 4푥 + 10푦 = 380，解得{푥 = 20 푦 = 30， 8 / 11 答：퐴、퐵两种花苗的单价分别是20元和30元； 设购买퐵花苗푥盆，则购买퐴花苗为(12 − 푥)盆，设总费用为푤元， 由题意得：푤＝20(12 − 푥) + (30 − 푥)푥＝−푥2 + 10푥 + 240(0 ≤ 푥 ≤ 12)， ∵1 < 0．故푤有最大值，当푥＝5时，푤的最小值为290，当푥＝0时，푤的最小值为240， 故本次购买至少准备240元，最多准备290元． 21.由푦＝푥2 − 4푥 + 3函数可知，푎1＝1，푏1＝−4，푐1＝3， ∵푎1 + 푎2＝0，푏1＝푏2，푐1 + 푐2＝0， ∴푎2＝−1，푏2＝−4，푐2＝−3， ∴函数푦＝푥2 − 4푥 + 3的“旋转函数”为푦＝−푥2 − 4푥 − 3； ∵푦＝5푥2 + (푚 − 1)푥 + 푛与푦＝−5푥2 − 푛푥 − 3互为“旋转函数”， ∴{푚 − 1 = −푛 푛 − 3 = 0 ， 解得：{푚 = −2 푛 = 3 ， ∴(푚 + 푛)2020＝(−2 + 3)2020＝1． 证明：当푥＝0时，푦＝2(푥 − 1)(푥 + 3)）＝−6， ∴点퐶的坐标为(0, −6)． 当푦＝0时，2(푥 − 1)(푥 + 3)＝0， 解得：푥1＝1，푥2＝−3， ∴点퐴的坐标为(1,  0)，点퐵的坐标为(−3,  0)． ∵点퐴，퐵，퐶关于原点的对称点分别是퐴1，퐵1，퐶1， ∴퐴1(−1,  0)，퐵1(3,  0)，퐶1(0,  6)． 设过点퐴1，퐵1，퐶1的二次函数解析式为푦＝푎(푥 + 1)(푥 − 3)， 将퐶1(0,  6)代入푦＝푎(푥 + 1)(푥 − 3)，得：6＝−3푎， 解得：푎＝−2， 过点퐴1，퐵1，퐶1的二次函数解析式为푦＝−2(푥 + 1)(푥 − 3)，即푦＝−2푥2 + 4푥 + 6． ∵푦＝2(푥 − 1)(푥 + 3)＝2푥2 + 4푥 − 6， ∴푎1＝2，푏1＝4，푐1＝−6，푎2＝−2，푏2＝4，푐2＝6， ∴푎1 + 푎2＝2 + (−2)＝0，푏1＝푏2＝4，푐1 + 푐2＝6 + (−6)＝0， ∴经过点퐴1，퐵1，퐶1的二次函数与函数푦＝2(푥 − 1)(푥 + 3)互为“旋转函数”． 22.600 72 2400 画树状图为： 共有12种等可能的结果数，其中他第二个吃的粽子恰好是퐴种粽子的结果数为3， 所以他第二个吃的粽子恰好是퐴种粽子的概率= 3 12 = 1 4 ． 23.，点퐵的坐标为(1,  0)， ∴푂퐴＝2，푂퐵＝1， 作퐷푀 ⊥ 푦轴于푀， ∵四边形퐴퐵퐶퐷是正方形， ∴∠퐵퐴퐷＝90∘，퐴퐵＝퐴퐷， ∴∠푂퐴퐵 + ∠퐷퐴푀＝90∘， ∵∠푂퐴퐵 + ∠퐴퐵푂＝90∘， ∴∠퐷퐴푀＝∠퐴퐵푂， 在△ 퐴푂퐵和△ 퐷푀퐴中 { ∠퐴퐵푂 = ∠퐷퐴푀 ∠퐴푂퐵 = ∠퐷푀퐴 = 90 퐴퐵 = 퐷퐴 ， ∴△ 퐴푂퐵 ≅△ 퐷푀퐴(퐴퐴푆)， ∴퐴푀＝푂퐵＝1，퐷푀＝푂퐴＝2， 9 / 11 ∴퐷(2， ， ∵双曲线푦 = 푘 푥 (푘 ≠ 0)经过퐷点， ∴푘＝2 × 3＝6， ∴双曲线为푦 = 6 푥 ， 设直线퐷퐸的解析式为푦＝푚푥 + 푛， 把퐵(1,  0)，퐷(2,（1）代入得{ 푚 + 푛 = 0 2푚 + 푛 = 3，解得{ 푚 = 3 푛 = −3， ∴直线퐷퐸的解析式为푦＝3푥 − 3； ((2)连接퐴퐶，交퐵퐷于푁， ∵四边形퐴퐵퐶퐷是正方形， ∴퐵퐷垂直平分퐴퐶，퐴퐶＝퐵퐷， 解{ 푦 = 3푥 − 3 푦 = 6 푥 得{푥 = 2 푦 = 3或{푥 = −1 푦 = −6， ∴퐸(−1, −(3)， ∵퐵(1,  0)，퐷(2,（4）， ∴퐷퐸 = √(2 + 1)2 + (3 + 6)2 = 3√10，퐷퐵 = √(2 − 1)2 + 32 = √10， ∴퐶푁 = 1 2 퐵퐷 = √10 2 ， ∴푆△퐷퐸퐶 = 1 2 퐷퐸 ⋅ 퐶푁 = 1 2 × 3√10 × √10 2 = 15 2 ． 24.证明：连接푂퐸，푂푃， ∵푃퐸 ⊥ 퐴퐵，点푄为弦퐸푃的中点， ∴퐴퐵垂直平分퐸푃， ∴푃퐵＝퐵퐸， ∵푂퐸＝푂푃，푂퐵＝푂퐵， ∴△ 퐵퐸푂 ≅△ 퐵푃푂(푆푆푆)， ∴∠퐵퐸푂＝∠퐵푃푂， ∵퐵푃为⊙ 푂的切线， ∴∠퐵푃푂＝90∘， ∴∠퐵퐸푂＝90∘， ∴푂퐸 ⊥ 퐵퐶， ∴퐵퐶是⊙ 푂的切线． ∵∠퐵퐸푂＝∠퐴퐶퐵＝90∘， ∴퐴퐶 // 푂퐸， ∴∠퐶퐴퐸＝∠푂퐸퐴， ∵푂퐴＝푂퐸， ∴∠퐸퐴푂＝∠퐴퐸푂， ∴∠퐶퐴퐸＝∠퐸퐴푂， ∴퐸퐹̂ = 퐸퐷̂ ． ∵퐴퐷为的⊙ 푂直径，点푄为弦퐸푃的中点， ∴퐸푃 ⊥ 퐴퐵， ∵퐶퐺 ⊥ 퐴퐵， ∴퐶퐺 // 퐸푃， ∵∠퐴퐶퐵＝∠퐵퐸푂＝90∘， ∴퐴퐶 // 푂퐸， ∴∠퐶퐴퐸＝∠퐴퐸푂， 10 / 11 ∵푂퐴＝푂퐸， ∴∠퐸퐴푄＝∠퐴퐸푂， ∴∠퐶퐴퐸＝∠퐸퐴푂， ∵∠퐴퐶퐸＝∠퐴푄퐸＝90∘，퐴퐸＝퐴퐸， ∴△ 퐴퐶퐸 ≅△ 퐴푄퐸(퐴퐴푆)， ∴퐶퐸＝푄퐸， ∵∠퐴퐸퐶 + ∠퐶퐴퐸＝∠퐸퐴푄 + ∠퐴퐻퐺＝90∘， ∴∠퐶퐸퐻＝∠퐴퐻퐺， ∵∠퐴퐻퐺＝∠퐶퐻퐸， ∴∠퐶퐻퐸＝∠퐶퐸퐻， ∴퐶퐻＝퐶퐸， ∴퐶퐻＝퐸푄， ∴四边形퐶퐻푄퐸是平行四边形， ∵퐶퐻＝퐶퐸， ∴四边形퐶퐻푄퐸是菱形， ∵sin∠퐴퐵퐶 = sin∠퐴퐶퐺 = 퐴퐺 퐴퐶 = 3 5 ， ∵퐴퐶＝15， ∴퐴퐺＝9， ∴퐶퐺 = √퐴퐶2 − 퐴퐺2 = 12， ∵△ 퐴퐶퐸 ≅△ 퐴푄퐸， ∴퐴푄＝퐴퐶＝15， ∴푄퐺＝6， ∵퐻푄2＝퐻퐺2 + 푄퐺2， ∴퐻푄2＝(12 − 퐻푄)2 + 62， 解得：퐻푄 = 15 2 ， ∴퐶퐻＝퐻푄 = 15 2 ， ∴四边形퐶퐻푄퐸的面积＝퐶퐻 ⋅ 퐺푄 = 15 2 × 6＝45． 25.∵抛物线푦＝푎푥2 + 푏푥 + 푐(푎 ≠ 0)的图象经过퐴(1,  0)，퐵(3,  0)， ∴设抛物线解析式为：푦＝푎(푥 − 1)(푥 − 3)， ∵抛物线푦＝푎(푥 − 1)(푥 − 3)(푎 ≠ 0)的图象经过点퐶(0,  6)， ∴6＝푎(0 − 1)(0 − 3)， ∴푎＝2， ∴抛物线解析式为：푦＝2(푥 − 1)(푥 − 3)＝2푥2 − 8푥 + 6； ∵푦＝2푥2 − 8푥 + 6＝2(푥 − 2)2 − 2， ∴顶点푀的坐标为(2, −2)， ∵抛物线的顶点푀与对称轴푙上的点푁关于푥轴对称， ∴点푁(2,  2)， 设直线퐴푁解析式为：푦＝푘푥 + 푏， 由题意可得：{ 0 = 푘 + 푏 2 = 2푘 + 푏， 解得：{ 푘 = 2 푏 = −2， ∴直线퐴푁解析式为：푦＝2푥 − 2， 联立方程组得：{ 푦 = 2푥 − 2 푦 = 2푥2 − 8푥 + 6， 11 / 11 解得：{푥1 = 1 푦1 = 0，{푥2 = 4 푦2 = 6， ∴点퐷(4,  6)， ∴푆△퐴퐵퐷 = 1 2 × 2 × 6＝6， 设点퐸(푚,  2푚 − 2)， ∵直线퐵퐸将△ 퐴퐵퐷的面积分为1: 2两部分， ∴푆△퐴퐵퐸 = 1 3 푆△퐴퐵퐷＝2或푆△퐴퐵퐸 = 2 3 푆△퐴퐵퐷＝4， ∴1 2 × 2 × (2푚 − 2)＝2或1 2 × 2 × (2푚 − 2)＝4， ∴푚＝2或3， ∴点퐸(2,  2)或(3,  4)； 若퐴퐷为平行四边形的边， ∵以퐴、퐷、푃、푄为顶点的四边形为平行四边形， ∴퐴퐷＝푃푄， ∴푥퐷 − 푥퐴＝푥푃 − 푥푄或푥퐷 − 푥퐴＝푥푄 − 푥푃， ∴푥푃＝4 − 1 + 2＝5或푥푃＝2 − 4 + 1＝−1， ∴点푃坐标为(5,  16)或(−1,  16)； 若퐴퐷为平行四边形的对角线， ∵以퐴、퐷、푃、푄为顶点的四边形为平行四边形， ∴퐴퐷与푃푄互相平分， ∴푥퐴+푥퐷 2 = 푥푃+푥푄 2 ， ∴푥푃＝3， ∴点푃坐标为(3,  0)， 综上所述：当点푃坐标为(5,  16)或(−1,  16)或(3,  0)时，使퐴、퐷、푃、푄为顶点的四边 形为平行四边形．