2020年山东省济南市历下区中考数学一模试卷 14页

第 1页 共 28页 ◎ 第 2页 共 28页 2020 年山东省济南市历下区中考数学一模试卷 一、选择题（本大题共 12 个小题，每小题 4 题，共 48 分．在每小题给出的四个选项中，只有一项是符合题 目要求的．） 1. 2020 的相反数是( ) A.2020 B.− 2020 C. 1 2020 D.− 1 2020 2. 下列立体图形中，俯视图与主视图不同的是（ ） A. B. C. D. 3. 2020 年 2 月 20 日下午，山东省第十二批援助湖北医疗队从济南遥墙机场集结，乘坐包机启程出征．千 余勇士赴荆楚，万难不辞战疫，山东已累计派出十二批医疗队 1797 人援助湖北，数字 1797 用科学记数法表 示为（ ） A.1.797 × 103 B.0.1797 × 104 C.1.797 × 104 D.17.97 × 102 4. 如图，已知 AB // DC，∠BED＝60∘ ，BC 平分∠ABE，则∠C 的度数是（ ） A.75∘ B.60∘ C.45∘ D.30∘ 5. 有理数 a，b 在数轴上表示如图所示，则下列各式中正确的是（ ） A.ab > 0 B.a + b < 0 C.b < a D.|b| > |a| 6. 下面在线学习平台的图标中，是轴对称图形的是（ ） A. B. C. D. 7. 下列运算正确的是（ ） A.x2 + x＝x3 B.( − 2x2)3＝8x6 C.(x − y)(x + y)＝x2 − y2 D.(x + 1)(x − 2)＝x2 − 2x − 2 8. 以下是某校九年级 10 名同学参加学校演讲比赛的统计表．则这组数据的众数和中位数分别为（ ） 成 绩 / 分 80 85 90 95 人 数 / 人 1 3 4 2 A.85，87.5 B.85，85 C.85，90 D.90，90 9. 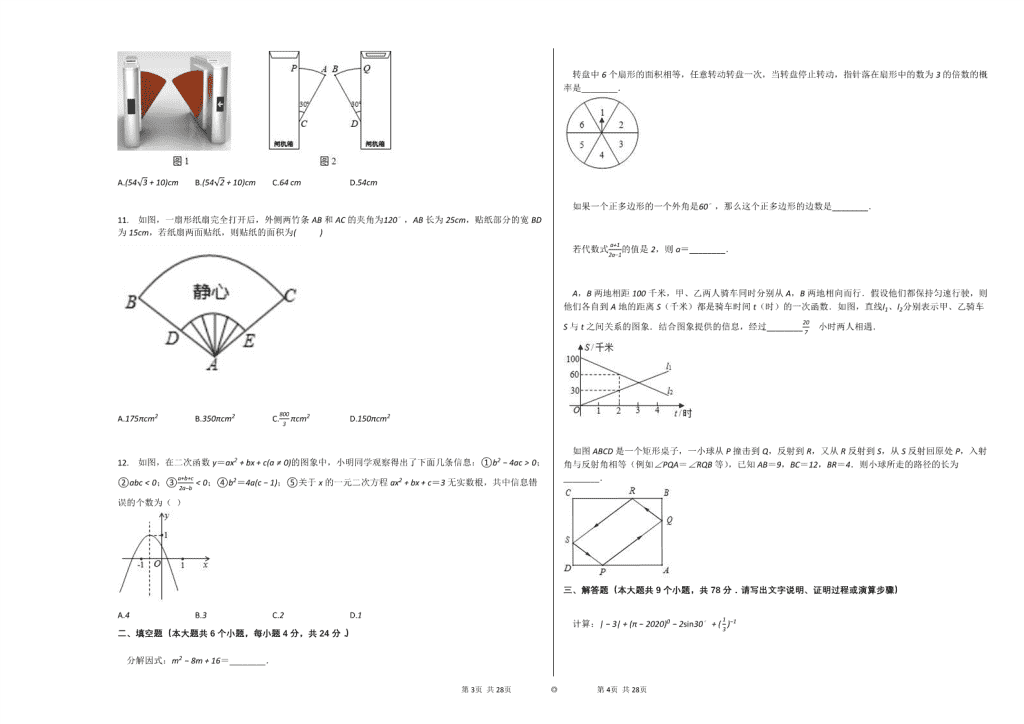已知反比例函数 y = k x 图象如图所示，下列说法正确的是( ) A.k > 0 B.y 随 x 的增大而减小 C.若矩形 OABC 面积为 2，则 k =− 2 D.若图象上两个点的坐标分别是 M ( − 2, y1 )，N( − 1, y2 )，则 y1 > y2 10. 图 1 是一个地铁站入口的双翼闸机．如图 2，它的双翼展开时，双翼边缘的端点 A 与 B 之间的距离为 10cm，双翼的边缘 AC＝BD＝54cm，且与闸机侧立面夹角∠PCA＝∠BDQ＝30∘ ．当双翼收起时，可以通过闸 机的物体的最大宽度为（ ） 第 3页 共 28页 ◎ 第 4页 共 28页 A.(54 3 + 10)cm B.(54 2 + 10)cm C.64 cm D.54cm 11. 如图，一扇形纸扇完全打开后，外侧两竹条 AB 和 AC 的夹角为120∘ ，AB 长为 25cm，贴纸部分的宽 BD 为 15cm，若纸扇两面贴纸，则贴纸的面积为( ) A.175πcm2 B.350πcm2 C.800 3 πcm2 D.150πcm2 12. 如图，在二次函数 y＝ax2 + bx + c(a ≠ 0)的图象中，小明同学观察得出了下面几条信息：①b2 − 4ac > 0； ②abc < 0；③a+b+c 2a−b < 0；④b2＝4a(c − 1)；⑤关于 x 的一元二次方程 ax2 + bx + c＝3 无实数根，共中信息错 误的个数为（ ） A.4 B.3 C.2 D.1 二、填空题（本大题共 6 个小题，每小题 4 分，共 24 分．） 分解因式：m2 − 8m + 16＝________． 转盘中 6 个扇形的面积相等，任意转动转盘一次，当转盘停止转动，指针落在扇形中的数为 3 的倍数的概 率是________． 如果一个正多边形的一个外角是60∘ ，那么这个正多边形的边数是________． 若代数式 a+1 2a−1 的值是 2，则 a＝________． A，B 两地相距 100 千米，甲、乙两人骑车同时分别从 A，B 两地相向而行．假设他们都保持匀速行驶，则 他们各自到 A 地的距离 S（千米）都是骑车时间 t（时）的一次函数．如图，直线l1、l2分别表示甲、乙骑车 S 与 t 之间关系的图象．结合图象提供的信息，经过________20 7 小时两人相遇． 如图 ABCD 是一个矩形桌子，一小球从 P 撞击到 Q，反射到 R，又从 R 反射到 S，从 S 反射回原处 P，入射 角与反射角相等（例如∠PQA＝∠RQB 等），已知 AB＝9，BC＝12，BR＝4．则小球所走的路径的长为 ________． 三、解答题（本大题共 9 个小题，共 78 分．请写出文字说明、证明过程或演算步骤） 计算：| − 3| + (π − 2020)0 − 2sin30∘ + ( 1 3 )−1 第 5页 共 28页 ◎ 第 6页 共 28页 解不等式组： 3x − 2 < x + 2 x−1 2 ≥− 1  ，并写出它的所有整数解． 如图，在平行四边形 ABCD 中，E，F 分别是对角线 BD 上的两点，且 BE＝DF．求证：AE＝CF． 为推进垃圾分类，推动绿色发展，某工厂购进甲、乙两种型号的机器人用来进行垃圾分类，甲型机器人比 乙型机器人每小时多分 20kg，甲型机器人分类 800kg 垃圾所用的时间与乙型机器人分类 600kg 垃圾所用的时 间相等． （1）两种机器人每小时分别分类多少垃圾？ （2）现在两种机器人共同分类 700kg 垃圾，工作 2 小时后甲型机器人因机器维修退出，求甲型机器人退出 后乙型机器人还需工作多长时间才能完成？ 如图，已知 AB 是⊙ O 的直径，DC 与⊙ O 相切于点 C，交 AB 的延长线于点 D． （1）求证：∠BAC＝∠BCD； （2）若 BD＝4，DC＝6，求⊙ O 的半径． 钟南山院士谈到防护新型冠状病毒肺炎时说：“我们需要重视防护，但也不必恐慌，尽量少去人员密集的场 所，出门戴口罩，在室内注意通风，勤洗手，多运动，少熬夜．”某社区为了加强社区居民对新型冠状病毒 肺炎防护知识的了解，通过微信群宣传新型冠状病毒肺炎的防护知识，并鼓励社区居民在线参与作答《2020 年新型冠状病毒防治全国统一考试（全国卷）》试卷（满分 10，社区管理员随机从有 400 人的某小区抽取 40 名人员的答卷成绩，并对他们的成绩（单位：分）统计如下： 85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75 80 60 80 95 85 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90 根据数据绘制了如下的表格和统计图： 等级 成绩(x) 频数 频率 A 90 < x ≤ 100 10 0.25 B 80 < x ≤ 90 a 0.35 C 70 < x ≤ 80 12 0.3 D 60 ≤ x ≤ 70 4 b 合计 40 1 根据上面提供的信息，回答下列问题： （1）统计表中的 a＝________，b＝________； （2）请补全条形统计图； （3）根据抽样调查结果，请估计该小区答题成绩为“C 级”的有多少人？ （4）该社区有 2 名男管理员和 2 名女管理员，现从中随机挑选 2 名管理员参加“社区防控”宣传活动，请用树 状图法或列表法求出恰好选中“1 男 1 女”的概率． 如图，已知反比例函数 y = m x (x > 0)的图象经过点 A(4, 2)，过 A 作 AC ⊥ y 轴于点 C．点 B 为反比例函数图象 上的一动点，过点 B 作 BD ⊥ x 轴于点 D，连接 AD．直线 BC 与 x 轴的负半轴交于点 E． 第 7页 共 28页 ◎ 第 8页 共 28页 （1）求反比例函数的表达式； （2）若 BD＝3OC，求△ BDE 的面积； （3）是否存在点 B，使得四边形 ACED 为平行四边形？若存在，请求出点 B 的坐标；若不存在，请说明理由． 如图①，在△ ABC 中，AB＝AC，∠BAC＝60∘ ，D 为 BC 边上一点（不与点 B，C 重合），将线段 AD 绕点 A 逆时针旋转60∘ 得到 AE，连接 EC，则： （1）①∠ACE 的度数是________； ②线段 AC，CD，CE 之间的数量关系是________． （2）如图②，在△ ABC 中，AB＝AC，∠BAC＝90∘ ，D 为 BC 边上一点（不与点 B，C 重合），将线段 AD 绕 点 A 逆时针旋转90∘ 得到 AE，连接 EC，请判断线段 AC，CD，CE 之间的数量关系，并说明理由； （3）如图②，AC 与 DE 交于点 F，在（2）条件下，若 AC＝8，求 AF 的最小值． 图①，抛物线 y＝− 2x2 + bx + c 过 A( − 1, 0)、B(3, 0)两点，交 y 轴于点 C，连接 BC． （1）求该抛物线的表达式和对称轴； （2）点 D 是抛物线对称轴上一动点，当△ BCD 是以 BC 为直角边的直角三角形时，求所有符合条件的点 D 的坐标； （3）如图 2，将抛物线在 BC 上方的图象沿 BC 折叠后与 y 轴交与点 E，求点 E 的坐 标． 第 9页 共 28页 ◎ 第 10页 共 28页 参考答案与试题解析 2020 年山东省济南市历下区中考数学一模试卷 一、选择题（本大题共 12 个小题，每小题 4 题，共 48 分．在每小题给出的四个选项中，只有一项是符合题 目要求的．） 1. 【答案】 B 【考点】 相反数 【解析】 直接利用相反数的定义得出答案． 【解答】 解：根据相反数的定义可知，2020 的相反数是：− 2020． 故选 B. 2. 【答案】 B 【考点】 简单几何体的三视图 【解析】 从正面看所得到的图形是主视图，从左面看到的图形是左视图，从上面看到的图象是俯视图． 【解答】 B．俯视图是圆，主视图是长方形，故选项 B 合题意（1）C．俯视图与主视图都是圆，故选项 C 不合题意（2） D．俯视图和主视图是长方形；故选项 D 不符合题意（3）故选：B． 3. 【答案】 A 【考点】 科学记数法--表示较大的数 【解析】 科学记数法的表示形式为 a × 10n的形式，其中 1 ≤ |a| < 10，n 为整数．确定 n 的值时，要看把原数变成 a 时， 小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值≥ 10 时，n 是正数；当原数的绝 对值< 1 时，n 是负数． 【解答】 1797＝1.797 × 103． 4. 【答案】 D 【考点】 平行线的性质 【解析】 根据平行线的性质得出∠ABE，根据角平分线定义求出∠ABC，根据平行线的性质得出∠C＝∠ABC，代入求 出即可． 【解答】 ∵ AB // DC，∠BED＝60∘ ， ∴ ∠ABE＝60∘ ， ∵ BC 平分∠ABE， ∴ ∠ABC = 1 2 ∠ABE＝30∘ ， ∵ AB // CD， ∴ ∠C＝∠ABC＝30∘ ， 5. 【答案】 B 【考点】 数轴 有理数的加法 绝对值 有理数的乘法 【解析】 根据数轴上点的位置确定出 a 与 b 的正负，以及绝对值的大小，再利用加法、乘法运算法则判断即可． 【解答】 由数轴上的位置得：a < 0 < b，且|a| > |b|， ∴ ab < 0，a + b < 0， 6. 【答案】 D 【考点】 轴对称图形 【解析】 根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对 称图形，这条直线叫做对称轴可得答案． 【解答】 A、不是轴对称图形，故此选项不合题意； B、不是轴对称图形，故此选项不合题意； C、不是轴对称图形，故此选项不合题意； D、是轴对称图形，故此选项符合题意； 7. 【答案】 C 【考点】 多项式乘多项式 幂的乘方与积的乘方 平方差公式 合并同类项 第 11页 共 28页 ◎ 第 12页 共 28页 【解析】 根据多项式乘多项式，合并同类项，幂的乘方与积的乘方，平方差公式等知识解答即可． 【解答】 A、x2与 x 不是同类项，不能合并，故此选项不符合题意； B、( − 2x2)3＝− 8x6，故此选项不符合题意； C、(x − y)(x + y)＝x2 − y2，故此选项符合题意； D、原式＝x2 − x − 2，故此选项不符合题意， 8. 【答案】 D 【考点】 众数 中位数 【解析】 先将数据从大到小从新排列，然后根据众数及中位数的定义求解即可． 【解答】 在这一组数据中 90 是出现次数最多的，故众数是 90． 而将这组数据从小到大的顺序排列后，处于中间位置的那个数是 90、90， 那么由中位数的定义可知，这组数据的中位数是 90． 9. 【答案】 C 【考点】 反比例函数系数 k 的几何意义 反比例函数的性质 【解析】 根据反比例函数的性质对 A、B、D 进行判断；根据反比例函数系数 k 的几何意义对 C 进行判断． 【解答】 解：A，反比例函数图象分布在第二、四象限，则 k < 0，所以 A 选项错误； B，在每一象限，y 随 x 的增大而增大，所以 B 选项错误； C，矩形 OABC 面积为 2，则|k| = 2，而 k < 0，所以 k =− 2，所以 C 选项正确； D，图象上两个点的坐标分别是 M ( − 2, y1 )，N( − 1, y2 )，则 y1 < y2，所以 D 选项错误． 故选 C. 10. 【答案】 C 【考点】 解直角三角形的应用-其他问题 【解析】 过 A 作 AE ⊥ CP 于 E，过 B 作 BF ⊥ DQ 于 F，则可得 AE 和 BF 的长，依据端点 A 与 B 之间的距离为 10cm， 即可得到可以通过闸机的物体的最大宽度． 【解答】 如图所示，过 A 作 AE ⊥ CP 于 E，过 B 作 BF ⊥ DQ 于 F，则 Rt △ ACE 中，AE = 1 2 AC = 1 2 × 54＝27(cm)， 同理可得，BF＝27cm， 又∵ 点 A 与 B 之间的距离为 10cm， ∴ 通过闸机的物体的最大宽度为 27 + 10 + 27＝64(cm)， 11. 【答案】 B 【考点】 扇形面积的计算 【解析】 贴纸部分的面积等于扇形 ABC 减去小扇形的面积，已知圆心角的度数为120∘ ，扇形的半径为 25cm 和 10cm， 可根据扇形的面积公式求出贴纸部分的面积． 【解答】 解：∵ AB = 25，BD = 15， ∴ AD = 10， ∴ S贴纸 = 120⋅ π×252 360 − 120⋅ π×102 360 = 175πcm2， ∵扇子双面贴纸， 故贴纸的面积为 175πcm2 × 2 = 350πcm2， 故选 B． 12. 【答案】 C 【考点】 抛物线与 x 轴的交点 二次函数图象与系数的关系 【解析】 根据二次函数的图象与性质即可求出答案． 【解答】 ①根据图象可知：△> 0， ∴ b2 − 4ac > 0，故①正确； ②由图象可知：a < 0，c > 0， 由对称轴可知：− b 2a < 0， ∴ b < 0， ∴ abc > 0，故②错误； ③由图象可知：− 1 <− b 2a < 0， ∴ 2a − b < 0， 当 x＝1 时，y < 0， ∴ a + b + c < 0， ∴ a+b+c 2a−b > 0，故③错误； ④由图象可知：当 x =− b 2a 时，y＝1， 第 13页 共 28页 ◎ 第 14页 共 28页 ∴ 4ac−b2 4a = 1， ∴ 4ac − b2＝4a， ∴ b2＝4a(c − 1)，故④正确； ⑤由于二次函数 y＝ax2 + bx + c(a ≠ 0)的最大值为 1， ∴ 关于 x 的一元二次方程 ax2 + bx + c＝3 无实数根，故⑤正确； 二、填空题（本大题共 6 个小题，每小题 4 分，共 24 分．） 【答案】 (m − 4)2 【考点】 因式分解-运用公式法 【解析】 直接利用完全平方公式进而分解因式得出答案． 【解答】 m2 − 8m + 16＝(m − 4)2． 【答案】 1 3 【考点】 概率公式 【解析】 直接利用概率公式计算可得答案． 【解答】 在这 6 个数字中，为 3 的倍数的有 3 和 6，共 2 个， ∴ 任意转动转盘一次，当转盘停止转动，指针落在扇形中的数为 3 的倍数的概率是2 6 = 1 3 ， 【答案】 6 【考点】 多边形内角与外角 【解析】 根据正多边形的每一个外角都相等，多边形的边数＝360∘ ÷ 60∘ ，计算即可求解． 【解答】 这个正多边形的边数：360∘ ÷ 60∘ ＝6． 【答案】 1 【考点】 解分式方程 【解析】 根据题意列出方程，求出方程的解即可得到 a 的值． 【解答】 根据题意得： a+1 2a−1 = 2， 去分母得：a + 1＝4a − 2， 移项合并得：3a＝3， 解得：a＝1， 经检验 a＝1 是分式方程的解， 【答案】 20 7 【考点】 一次函数的应用 【解析】 利用待定系数法求出直线l1、l2的解析式，利用两函数相等进而求出相遇的时间． 【解答】 设l1的关系式为：s1＝kt，则 30＝k × 2，解得：k＝15，故s1＝15t； 设s2＝at + b，将(0, 100)，(2, 60)， 则 b = 100 2a + b = 60  ， 解得： a =− 20 b = 100  ， 故l2的关系式为s2＝− 20t + 100； 15t＝− 20t + 100， t = 20 7 ． 即他们经过20 7 小时两人相遇． 【答案】 30 【考点】 生活中的轴对称现象 矩形的性质 【解析】 证明四边形 SPQR 是平行四边形，推出 SR＝PQ，PS＝QR，证三角形全等得出 SR＝PQ，RQ＝PS，根据相似求 出 DS，根据勾股定理求出即 RS，RQ，PQ，SP 即可． 【解答】 ∵ 入射角与反射角相等， ∴ ∠BQR＝∠AQP，∠APQ＝∠SPD，∠CSR＝∠DSP，∠CRS＝∠BRQ， ∵ 四边形 ABCD 是矩形， ∴ ∠A＝∠B＝∠C＝∠D＝90∘ ， ∴ ∠DPS + ∠DSP＝90∘ ，∠AQP + ∠APQ＝90∘ ， ∴ ∠DSP＝∠AQP＝∠CSR＝∠BQR， ∴ ∠RSP＝∠RQP， 同理∠SRQ＝∠SPQ， ∴ 四边形 SPQR 是平行四边形， ∴ SR＝PQ，PS＝QR， 在△ DSP 和△ BQR 中 ∠BQR = ∠DSP ∠D = ∠B PS = RQ  ， ∴ △ DSP ≅ △ BQR(AAS)， ∴ BR＝DP＝4，BQ＝DS， 第 15页 共 28页 ◎ 第 16页 共 28页 ∵ 四边形 ABCD 是矩形， ∴ AB＝CD＝9，BC＝AD＝112， ∴ AQ＝9 − DS，AP＝12 − 4＝8， ∵ ∠SPD＝∠APQ， ∴ △ SDP ∽△ QAP， ∴ DP DS = AP AQ ， ∴ 4 DS = 8 9−DS ， DS＝3， 在 Rt △ DSP 中，由勾股定理得：PS＝QR = DS2 + DP2 = 32 + 42 = 5， 同理 PQ＝RS＝10， ∴ QP + PS + SR + QR＝2 × 5 + 2 × 10＝30， 三、解答题（本大题共 9 个小题，共 78 分．请写出文字说明、证明过程或演算步骤） 【答案】 | − 3| + (π − 2020)0 − 2sin30∘ + ( 1 3 )−1 ＝3 + 1 − 2 × 1 2 + 3 ＝6 【考点】 实数的运算 零指数幂、负整数指数幂 零指数幂 特殊角的三角函数值 【解析】 首先计算乘方，然后计算乘法、除法，最后从左向右依次计算，求出算式的值是多少即可． 【解答】 | − 3| + (π − 2020)0 − 2sin30∘ + ( 1 3 )−1 ＝3 + 1 − 2 × 1 2 + 3 ＝6 【答案】 3x − 2 < x + 2 x−1 2 ≥− 1  ， 解①得 x < 2， 解②得 x ≥− 1． 不等式组的解集是− 1 ≤ x < 2． 则整数解是− 1，0，1． 【考点】 解一元一次不等式组 一元一次不等式组的整数解 【解析】 首先解每个不等式，把解集在数轴上表示出来即可得到不等式组的解集，然后确定解集中的整数即可． 【解答】 3x − 2 < x + 2 x−1 2 ≥− 1  ， 解①得 x < 2， 解②得 x ≥− 1． 不等式组的解集是− 1 ≤ x < 2． 则整数解是− 1，0，1． 【答案】 证明：∵ 四边形 ABCD 是平行四边形， ∴ AB＝CD，AB // CD． ∴ ∠ABE＝∠CDF． 在△ ABE 和△ DCF 中， AB = CD ∠ABE = ∠CDF BE = DF  ， ∴ △ ABE ≅ △ DCF(SAS)． ∴ AE＝CF． 【考点】 全等三角形的性质与判定 平行四边形的性质 【解析】 根据已知条件利用 SAS 来判定△ ABE ≅ △ DCF，从而得出 AE＝CF． 【解答】 证明：∵ 四边形 ABCD 是平行四边形， ∴ AB＝CD，AB // CD． ∴ ∠ABE＝∠CDF． 在△ ABE 和△ DCF 中， AB = CD ∠ABE = ∠CDF BE = DF  ， ∴ △ ABE ≅ △ DCF(SAS)． ∴ AE＝CF． 【答案】 甲型机器人每小时分类 80kg 垃圾．则乙型机器人每小时分类 60kg 垃圾， 甲型机器人退出后乙型机器人还需要工作 7 小时 【考点】 分式方程的应用 【解析】 （1）设甲型机器人每小时分类 xkg 垃圾．则乙型机器人每小时分类(x − 20)kg 垃圾，根据列出方程即可求出 第 17页 共 28页 ◎ 第 18页 共 28页 答案． （2）根据条件列出算式即可求出答案． 【解答】 设甲型机器人每小时分类 xkg 垃圾．则乙型机器人每小时分类(x − 20)kg 垃圾， 由题意得：800 x = 600 x−20 ， 解得：x＝80， 检验：当 x＝80 时，x(x − 20) ≠ 0， 所以，原分式方程的解为 x＝80， x − 20＝80 − 20 − 60， 答：甲型机器人每小时分类 80kg 垃圾．则乙型机器人每小时分类 60kg 垃圾， [700 − (80 + 60) × 2] ÷ 60＝7 小时， 答：甲型机器人退出后乙型机器人还需要工作 7 小时． 【答案】 如图，连接 OC． 证明：∵ DC 与⊙ O 相切， ∠OCD＝∠OCB + ∠BCD＝90∘ ， ∵ AB 是⊙ O 的直径， ∴ ∠ACB＝∠OCB + ∠ACO＝90∘ ， ∴ ∠ACO＝∠BCD ∵ OA＝OC， ∴ ∠ACO＝∠BAC， ∴ ∠BAC＝∠BCD； 由（1）可得，∠BAC＝∠BCD； ∵ ∠CDB＝∠ADC， ∴ △ CDB ∽△ ADC， ∴ BD DC = DC AD ，即4 6 = 6 AD ， ∴ DA＝9 ∴ AB＝DA − BD＝9 − 4＝5， ∴ ⊙ O 的半径为5 2 ． 【考点】 切线的性质 圆周角定理 【解析】 （1）根据直径所对的圆周角为直角以及圆的切线垂直于经过切点的半径，可得∠OCD＝∠OCB + BCD＝90∘ ， ∠ACB＝∠OCB + ACO＝90∘ ，于是∠ACO＝∠BCD，又 OA＝OC，所以∠ACO＝∠BAC，因此∠BAC＝∠BCD； （2）易证∴ △ CDB ∽△ ADC，由 BD＝4，DC＝6 通过相似比求出 DA 的长，然后求出 AB，从而求出⊙ O 的半径． 【解答】 如图，连接 OC． 证明：∵ DC 与⊙ O 相切， ∠OCD＝∠OCB + ∠BCD＝90∘ ， ∵ AB 是⊙ O 的直径， ∴ ∠ACB＝∠OCB + ∠ACO＝90∘ ， ∴ ∠ACO＝∠BCD ∵ OA＝OC， ∴ ∠ACO＝∠BAC， ∴ ∠BAC＝∠BCD； 由（1）可得，∠BAC＝∠BCD； ∵ ∠CDB＝∠ADC， ∴ △ CDB ∽△ ADC， ∴ BD DC = DC AD ，即4 6 = 6 AD ， ∴ DA＝9 ∴ AB＝DA − BD＝9 − 4＝5， ∴ ⊙ O 的半径为5 2 ． 【答案】 14,0.1 如图即为补全的条形统计图； 0.3 × 400＝120（名） 答：估计该小区答题成绩为“C 级”的有 120 人； 第 19页 共 28页 ◎ 第 20页 共 28页 如图， 根据树状图可知： 所有可能的结果共有 12 种， 恰好选中“1 男 1 女”的有 8 种， ∴ 恰好选中“1 男 1 女”的概率为 8 12 = 2 3 ． 【考点】 频数（率）分布表 列表法与树状图法 条形统计图 用样本估计总体 【解析】 （1）根据题中数据即可求得 a、b 的值； （2）根据（1）中表格数据即可补全条形统计图； （3）根据（1）结果，即可用样本估总体，可得该小区答题成绩为“C 级”人数； （4）根据树状图法求即可求出恰好选中“1 男 1 女”的概率． 【解答】 由题意可知： B 等级的频数 a＝14， ∴ B 等级的频率为：14 ÷ 40＝0.35， D 等级的频数为 4， b＝1 − 0.25 − 0.35 − 0.3＝0.1． 故答案为：14、0.1、4、0.35； 如图即为补全的条形统计图； 0.3 × 400＝120（名） 答：估计该小区答题成绩为“C 级”的有 120 人； 如图， 根据树状图可知： 所有可能的结果共有 12 种， 恰好选中“1 男 1 女”的有 8 种， ∴ 恰好选中“1 男 1 女”的概率为 8 12 = 2 3 ． 【答案】 ∵ 反比例函数 y = m x (x > 0)的图象经过点 A(4, 2)， ∴ m＝8， ∴ 反比例函数 y = 8 x (x > 0)． ∵ AC ⊥ y 轴，A(4, 2)， ∴ OC＝2， ∵ BD＝3OC， ∴ BD＝6， ∵ BD ⊥ x 轴， ∴ B( 4 3 , 6)， ∵ C(0, 2)， 设直线 BC 的解析式为 y＝kx + b，则有 b = 2 4 3 k + b = 6  ， 解得 k = 3 b = 2  ， ∴ 直线 BC 的解析式为 y＝3x + 2， ∴ E( − 2 3 , 0)， ∴ DE = 2 3 + 4 3 = 2， ∴ S△BED = 1 2 × DE × BD＝6． 存在．如图，设 BD 交 AC 于 F．设 B(a,  8 a )， ∵ A(4, 2) ∴ AC＝4， ∵ 四边形 ACED 是平行四边形， ∴ DE＝AC＝4，且 CF // DE， ∴ △ BCF ∽△ BED， ∴ CF DE = BF BD ，即a 4 = 8 a−2 8 a ，解得 a＝2， 第 21页 共 28页 ◎ 第 22页 共 28页 ∴ B(2, 4)． 【考点】 反比例函数综合题 【解析】 （1）利用待定系数法即可解决问题． （2）求出直线 BC 的解析式，可得 E 点坐标，求出 DE，BD 即可解决问题． （3）设 B(a,  8 a )，由平行四边形的性质可得△ BCF ∽△ BED，利用相似三角形的性质可求得 a 的值，则可求 得 B 点坐标． 【解答】 ∵ 反比例函数 y = m x (x > 0)的图象经过点 A(4, 2)， ∴ m＝8， ∴ 反比例函数 y = 8 x (x > 0)． ∵ AC ⊥ y 轴，A(4, 2)， ∴ OC＝2， ∵ BD＝3OC， ∴ BD＝6， ∵ BD ⊥ x 轴， ∴ B( 4 3 , 6)， ∵ C(0, 2)， 设直线 BC 的解析式为 y＝kx + b，则有 b = 2 4 3 k + b = 6  ， 解得 k = 3 b = 2  ， ∴ 直线 BC 的解析式为 y＝3x + 2， ∴ E( − 2 3 , 0)， ∴ DE = 2 3 + 4 3 = 2， ∴ S△BED = 1 2 × DE × BD＝6． 存在．如图，设 BD 交 AC 于 F．设 B(a,  8 a )， ∵ A(4, 2) ∴ AC＝4， ∵ 四边形 ACED 是平行四边形， ∴ DE＝AC＝4，且 CF // DE， ∴ △ BCF ∽△ BED， ∴ CF DE = BF BD ，即a 4 = 8 a−2 8 a ，解得 a＝2， ∴ B(2, 4)． 【答案】 60∘ ,AC＝CD + CE 在△ ABC 中，AB＝AC，∠BAC＝90∘ ， ∴ BC = 2AC， 由旋转知，AD＝AE，∠DAE＝90∘ ＝∠BAC， ∴ ∠BAD＝∠CAE， ∴ △ ABD ≅ △ ACE(SAS)， ∴ BD＝CE， ∴ BC＝BD + CD＝CE + CD， ∴ 2AC＝CE + CD； 由（2）知，△ ABD ≅ △ ACE， ∴ ACE＝∠ABD， 在△ ABC 中，AB＝AC，∠BAC＝90∘ ， ∴ ∠ABD＝∠ACB＝45∘ ， ∴ ∠ACE＝45∘ ， ∴ ∠BCE＝∠ACB + ∠ACE＝90∘ ， ∵ ∠DAE＝90∘ ， ∴ ∠BCE + ∠DAE＝180∘ ， ∴ 点 A，D，C，E 在以 DE 为直径的圆上， ∵ AC 与 DE 交于点 F， ∴ AF 是直径 DE 上的一点到点 A 的距离， 即：当 AF ⊥ DE 时，AF 最小， ∴ ∠CFD＝90∘ ， ∴ ∠CDF＝90∘ − ∠ACB＝45∘ ， ∵ ∠ADE＝45∘ ， ∴ ∠ADC＝90∘ ， ∴ 四边形 ADCE 是矩形， ∴ AF 最小= 1 2 AC＝4． 第 23页 共 28页 ◎ 第 24页 共 28页 【考点】 几何变换综合题 【解析】 （1）①先判断出∠BAD＝∠CAE，即可判断出△ ABD ≅ △ ACE，即可得出结论； ②由①得，△ ABD ≅ △ ACE，得出 BD＝CE，即可得出结论； （2）先判断出 BC = 2AC，再同（1）的方法判断出△ ABD ≅ △ ACE，即可得出结论； （3）先判断出点 A，D，C，E 四点共圆，再由 AF 最小判断出四边形 ADCE 是矩形，即可得出结论． 【解答】 ①∵ △ ABC 是等边三角形， ∴ AB＝AC，∠B＝∠BAC＝60∘ ， 由旋转知，AD＝AE，∠DAE＝60∘ ＝∠BAC， ∴ ∠BAD＝∠CAE， ∴ △ ABD ≅ △ ACE(SAS)， ∴ ∠ACE＝∠B＝60∘ ， 故答案为60∘ ； ②由（1）知，△ ABD ≅ △ ACE， ∴ BD＝CE， ∴ BC＝BD + CD＝CE + CD， ∵ △ ABC 是等边三角形， ∴ AC＝BC， ∴ AC＝CE + CD， 故答案为 AC＝CE + CD； 在△ ABC 中，AB＝AC，∠BAC＝90∘ ， ∴ BC = 2AC， 由旋转知，AD＝AE，∠DAE＝90∘ ＝∠BAC， ∴ ∠BAD＝∠CAE， ∴ △ ABD ≅ △ ACE(SAS)， ∴ BD＝CE， ∴ BC＝BD + CD＝CE + CD， ∴ 2AC＝CE + CD； 由（2）知，△ ABD ≅ △ ACE， ∴ ACE＝∠ABD， 在△ ABC 中，AB＝AC，∠BAC＝90∘ ， ∴ ∠ABD＝∠ACB＝45∘ ， ∴ ∠ACE＝45∘ ， ∴ ∠BCE＝∠ACB + ∠ACE＝90∘ ， ∵ ∠DAE＝90∘ ， ∴ ∠BCE + ∠DAE＝180∘ ， ∴ 点 A，D，C，E 在以 DE 为直径的圆上， ∵ AC 与 DE 交于点 F， ∴ AF 是直径 DE 上的一点到点 A 的距离， 即：当 AF ⊥ DE 时，AF 最小， ∴ ∠CFD＝90∘ ， ∴ ∠CDF＝90∘ − ∠ACB＝45∘ ， ∵ ∠ADE＝45∘ ， ∴ ∠ADC＝90∘ ， ∴ 四边形 ADCE 是矩形， ∴ AF 最小= 1 2 AC＝4． 【答案】 ∵ 抛物线 y＝− 2x2 + bx + c 过 A( − 1, 0)、B(3, 0)两点， ∴ − 2 × ( − 1)2 − b + c = 0 − 2 × 32 + 3b + c = 0  ，得 b = 4 c = 6  ， ∴ y＝− 2x2 + 4x + 6＝− 2(x − 1)2 + 8， ∴ 抛物线的对称轴是直线 x＝1， 即该抛物线的解析式为 y＝− 2x2 + 4x + 6，对称轴是直线 x＝1； 分两种情况： 设点 D 的坐标为(1, y) 第一种情况是：∠BCD＝90∘ 时， 则 CD2 + BC2＝BD2， ∵ 点 B 的坐标为(3, 0)，抛物线 y＝− 2x2 + 4x + 6 交 y 轴于点 C， ∴ 点 C 的坐标为(0, 6)， ∴ [12 + (y − 6)2] + (32 + 62)＝(3 − 1)2 + y2， 解得，y＝6.5， ∴ 点 D 的坐标为(1, 6.5)； 第二种情况：当∠DBC＝90∘ 时， BD2 + BC2＝CD2， 即[(3 − 1)2 + y2] + (32 + 62)＝12 + (6 − y)2， 解得，y＝− 1， ∴ 点 D 的坐标为(1,  − 1)， 综上所述，符合条件的点 D 的坐标为(1, 6.5)，(1,  − 1)； 因为点 C 的坐标为(0, 6)，点 B 的坐标为(3, 0)， 设直线 BC 的解析式为 y＝kx + 6， 则 3k + 6＝0，得 k＝− 2， 即直线 BC 的解析式为 y＝− 2x + 6， 如右图所示，作点 E 关于直线 BC 的对称点 E′交 BC 于点 F，过点 F 作 FN ⊥ y 轴于点 N， 设 E(0, m)，E′(x, y)， 则 EE′ ⊥ BC， ∴ ∠CFE＝∠COB＝90∘ ， ∴ BC = 32 + 62 = 3 5， ∵ ∠ECF＝∠BCO， ∴ △ ECF ∽△ BCO， ∴ CE CB = CF CO ， 即6−m 3 5 = CF 6 ， 解得，CF = 2 5(6−m) 5 ， 又∵ ∠CNF＝∠COB，∠NCF＝∠OCB， ∴ △ NCF ∽△ OCB， ∴ FN BO = CF CB ， 第 25页 共 28页 ◎ 第 26页 共 28页 即FN 3 = 2 5(6−m) 5 3 5 ， 解得，FN = 2(6−m) 5 ， ∴ 点 F 的横坐标为2(6−m) 5 ， 把 x = 2(6−m) 5 代入直线 BC 的解析式，得 y = 4m+6 5 ， ∴ 点 F 的坐标为( 2(6−m) 5 ,  4m+6 5 )， ∵ EE′关于直线 BC 对称， ∴ 点 F 为 EE′的中点， ∴ x 2 = 2(6−m) 5 m+y 2 = 4m+6 5  ， 解得 x = 4(6−m) 5 y = 12+3m 5  ， ∴ E′( 4(6−m) 5 ,  12+3m 5 )， ∵ 点 E′在抛物线 y＝− 2x2 + 4x + 6 上， ∴ 12+3m 5 =− 2 × [ 4(6−m) 5 ]2 + 4 × 4(6−m) 5 + 6， 解得，m1＝6，m2 = 97 32 ， ∵ 点 C(0, 6)，点 E 在点 C 下方， ∴ 点 E 的坐标为(0,  97 32 )． 【考点】 二次函数综合题 【解析】 （1）根据抛物线 y＝− 2x2 + bx + c 过 A( − 1, 0)、B(3, 0)两点，可以求得该抛物线的解析式，然后将解析式化为 顶点式即可得到该抛物线的对称轴； （2）根据题意，可知分两种情况，然后利用勾股定理可求得点 D 的坐标； （3）根据题意和折叠的性质，作出点 E 关于 BC 的对称点 E′，再根据二次函数的解析式，可以求得 E′的坐标， 再根据直线 BC 和 E、E′的关系可以求得点 E 的坐标． 【解答】 ∵ 抛物线 y＝− 2x2 + bx + c 过 A( − 1, 0)、B(3, 0)两点， ∴ − 2 × ( − 1)2 − b + c = 0 − 2 × 32 + 3b + c = 0  ，得 b = 4 c = 6  ， ∴ y＝− 2x2 + 4x + 6＝− 2(x − 1)2 + 8， ∴ 抛物线的对称轴是直线 x＝1， 即该抛物线的解析式为 y＝− 2x2 + 4x + 6，对称轴是直线 x＝1； 分两种情况： 设点 D 的坐标为(1, y) 第一种情况是：∠BCD＝90∘ 时， 则 CD2 + BC2＝BD2， ∵ 点 B 的坐标为(3, 0)，抛物线 y＝− 2x2 + 4x + 6 交 y 轴于点 C， ∴ 点 C 的坐标为(0, 6)， ∴ [12 + (y − 6)2] + (32 + 62)＝(3 − 1)2 + y2， 解得，y＝6.5， ∴ 点 D 的坐标为(1, 6.5)； 第二种情况：当∠DBC＝90∘ 时， BD2 + BC2＝CD2， 即[(3 − 1)2 + y2] + (32 + 62)＝12 + (6 − y)2， 解得，y＝− 1， ∴ 点 D 的坐标为(1,  − 1)， 综上所述，符合条件的点 D 的坐标为(1, 6.5)，(1,  − 1)； 因为点 C 的坐标为(0, 6)，点 B 的坐标为(3, 0)， 设直线 BC 的解析式为 y＝kx + 6， 则 3k + 6＝0，得 k＝− 2， 即直线 BC 的解析式为 y＝− 2x + 6， 如右图所示，作点 E 关于直线 BC 的对称点 E′交 BC 于点 F，过点 F 作 FN ⊥ y 轴于点 N， 设 E(0, m)，E′(x, y)， 则 EE′ ⊥ BC， ∴ ∠CFE＝∠COB＝90∘ ， ∴ BC = 32 + 62 = 3 5， ∵ ∠ECF＝∠BCO， ∴ △ ECF ∽△ BCO， ∴ CE CB = CF CO ， 即6−m 3 5 = CF 6 ， 解得，CF = 2 5(6−m) 5 ， 又∵ ∠CNF＝∠COB，∠NCF＝∠OCB， ∴ △ NCF ∽△ OCB， 第 27页 共 28页 ◎ 第 28页 共 28页 ∴ FN BO = CF CB ， 即FN 3 = 2 5(6−m) 5 3 5 ， 解得，FN = 2(6−m) 5 ， ∴ 点 F 的横坐标为2(6−m) 5 ， 把 x = 2(6−m) 5 代入直线 BC 的解析式，得 y = 4m+6 5 ， ∴ 点 F 的坐标为( 2(6−m) 5 ,  4m+6 5 )， ∵ EE′关于直线 BC 对称， ∴ 点 F 为 EE′的中点， ∴ x 2 = 2(6−m) 5 m+y 2 = 4m+6 5  ， 解得 x = 4(6−m) 5 y = 12+3m 5  ， ∴ E′( 4(6−m) 5 ,  12+3m 5 )， ∵ 点 E′在抛物线 y＝− 2x2 + 4x + 6 上， ∴ 12+3m 5 =− 2 × [ 4(6−m) 5 ]2 + 4 × 4(6−m) 5 + 6， 解得，m1＝6，m2 = 97 32 ， ∵ 点 C(0, 6)，点 E 在点 C 下方， ∴ 点 E 的坐标为(0,  97 32 )．