中考数学专题复习练习：角的平分线 10页

例01．已知：如图，BD是的平分线，，P在BD上，，. ‎ 求证：. ‎ 分析：要证，可以证明点P在的平分线上. ‎ 证明：因为BD是的平分线，‎ 所以. ‎ 在和中，‎ 所以，‎ 所以（全等三角形的对应角相等）‎ 因为，‎ 所以（角平分线上的点到角的两边距离相等）‎ 说明 本题也可以在证明了后再证明. 但利用角平分线的性质定理来证明更简洁. ‎ 今后证明一定要注意灵活运用所学知识. ‎ 例02．已知：如图，PA、PC分别是外角和的角平分线，它们交于P. ‎ 求证：PB为的角平分线. ‎ 分析：要证BP为的角平分线，只须证点P到BM、BN距离相等，而PA、PC为外角平分线，故可过P作，，. ‎ 证明：过点P作，，于F. 因为PA、PC分别是和的平分线，且，，‎ ‎∴，（角平分线上的点到角两边距离相等）. ‎ ‎∴. ‎ 又∵，‎ ‎∴点P在的角平分线上（到角两边距离相等的点在这个角的平分线上）‎ ‎∴BP为的角平分线. ‎ 说明 当有角平分线这个条件时，常常经过角平分线上的点向角的两边作垂线，利用“角平分线上的点到角两边距离相等”来证题. 同样，要证明某射线是角平分线时，只要经过射线上一点向角的两边作垂线，再证垂线段相等. ‎ 本题不能只想到应用三角形全等来解决总是，防止形成思维误区. ‎ 例03．如图，已知：AD是的角平分线，DE、DF分别是和的高.‎ ‎ 求证：. ‎ 分析：因为AD为的角平分线，DE、DF是点D到AB、AC边上的距离，∴有. 再利用直角三角形全等可证明. ‎ 证明：AD是的角平分线，DE、DF分别是和的高. ‎ ‎∴ （角平分线上的一点到这个角的两边的距离相等）‎ 在和中，‎ ‎∴ ‎ ‎∴ （全等三角形的对应边相等）‎ 说明：本题也可以用AAS来证明三角形全等，但直接使用角平分线的性质更简单. 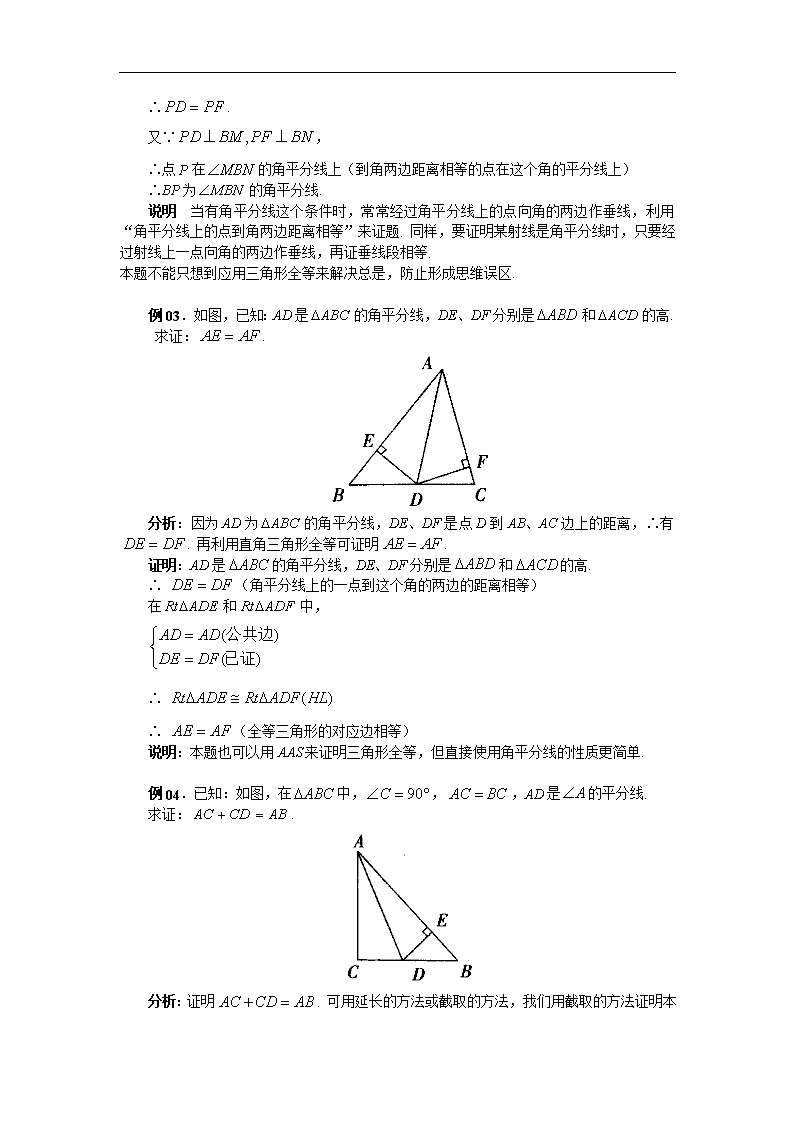‎ 例04．已知：如图，在中，，，AD是的平分线. ‎ 求证：. ‎ 分析：证明. 可用延长的方法或截取的方法，我们用截取的方法证明本 题. 在AB上取一点E，使，则易证，由此 得到，，又由，得. 可证明本命题，那么利用角平分线的性质，作辅助线的时候，也可作于E，可直接得到. ‎ 证明：过D点作垂足为E. 则 ‎∵AD为角平分线，‎ ‎∴（角平分线上的一点到这个角的两边的距离相等）‎ 在和中，‎ ‎，‎ ‎∴ （全等三角形的对应边相等）‎ ‎∵ （已知），（已知）‎ ‎∴ ‎ 在中，，，‎ ‎∴. ‎ ‎∴‎ ‎∵， ‎ ‎∴. ‎ 例05．已知：如图，在中，AD平分，于E，于F. ‎ 求证：. ‎ 分析：欲证：，就要证 所以考虑证 由题中条件可知、已有一边（公共边）一角对应相等，只要证即可，所以先证明 证明：∵AD是的平分线. ，‎ ‎∴ （角平分线上的点到这个两边距离相等）‎ 在和中 ‎∴‎ ‎∴（全等三角形的对应边相等）‎ 在和中 ‎∴‎ ‎∴ （全等三角形对应角相等）‎ ‎∴ ‎ ‎∴ （垂直定义）‎ 例06．已知：如图，在中，BE、CF分别平分、，且交于点O，‎ 求证：点O在的平分线上. ‎ 分析：要证点O在的平分线上，只需证明点O到的两边的距离相等，即证. ‎ 证明：过点O分别作三边的垂线OD、OG、OH，‎ ‎∵，BO平分（已知）‎ ‎∴（角平分线上的点到这个角两边的距离相等）‎ 同理，‎ ‎∴‎ ‎∴点O在的平分线上（到角两边距离相等的点在这个角的平分线上）‎ 例07．写出下列命题的逆命题，并判断真假. ‎ ‎（1）同位角相等，两直线平行. ‎ ‎（2）如果，那么 ‎（3）如果是直角三角形，那么当每个内角取一个对应外角时，三角形的三个外角只有两个钝角. ‎ ‎（4）如果，那么，，. ‎ 分析：准确理解原命题、逆命题、真命题、假命题等概念，分清题设和结论，是写出逆命题的关键，对于假命题，可以举一个反例，全面地考虑问题. ‎ 解答：（1）逆命题是：两直线平行，同位角相等，它是一个真命题. ‎ ‎（2）逆命题是：如果，那它是一个假命题 ‎∵，∴或 ‎（3）逆命题是：如果的三个外角中只有两个钝角，那么是直角三角形. 它是一个假命题，因为还可能是钝角三角形. ‎ ‎（4）逆命题是：如果和中，，，，那么，这是一个假命题，因为有两边及其一边的对角对应相等的两个三角形不一定是全等三角形. ‎ 角的平分线 A B C M N P 图1‎ 例1、已知：如图1，△ABC的角平分线BM、CN相交于点P.‎ 求证：点P到三边AB、BC、CA的距离相等.‎ 分析：这是证明线段相等问题，由已知利用定理不难证明.‎ 证明：（略）‎ 说明：已知、求证中都没有具体说明哪些线段是距离，证明它们相等必须标出它们，这一段话要在证明中写出，同辅助线一样处理。‎ E A B C P H G 图2‎ 例2、已知：如图2，PB、PC分别是△ABC的外角平分线，相交于点P.‎ 求证：P在∠A的平分线上 分析：要证结论成立，需要证明P到∠A两边的距离相等，‎ 所以作PE⊥AB于E、PG⊥AC于G，‎ 为证PE＝PG，考虑利用已知的两个角平分线，‎ 自然应再作PH⊥BC于H，此时易于发现PE＝PH，PH＝PG.‎ 证明：（略）‎ 说明：解题关键是标出距离，运用角平分线性质定理的逆定理求证。‎ 例3、写出下列命题的逆命题，并判断它们是真命题还是假命题 （1） 全等三角形的对应角相等；‎ （2） 对顶角相等 （3） 如果那么 （4） 直角三角形的两个锐角互余 分析：写出一个命题的逆命题的关键是分清它的题设和结论。然后将其“换位”；判断一个命题为真要证明，为假要举反例。‎ 解：它们的逆命题分别是：‎ （1） 三个角对应相等的两个三角形全等 （2） 如果两个角相等，那么这两个角是对顶角 （3） 如果，那么 （4） 有两个锐角互为余角的三角形是直角三角形 其中（1）、（2）、（3）为假命题，而（4）为真命题，证明略。‎ 说明：“如果”、“那么”这是标明条件和结论的关键词，若题目没有需转化成这样的句式。‎ 例4、已知：如图3，PB⊥AB，PC⊥AC，PB＝PC，D是AP上一点 求证：∠BDP＝∠CDP 分析：要证结论成立，只需证△BDP与△CDP全等，‎ 这可由条件不难证得。‎ 证明：‎ D A B C P 图3‎ 说明：本题的证法说明证明角平分线，不一定都要用其判定定理。‎ 选择题 ‎（1）下列命题中的假命题是（ ）‎ ‎（A）等腰直角三角形是直角三角形 ‎（B）等边三角形是等腰三角形 ‎（C）等腰三角形是锐角三角形 ‎（D）等边三角形是锐角三角形 ‎（2）下列说法正确的是（ ）‎ ‎（A）每个命题都有逆命题 （B）每个定理都有逆定理 ‎（C）真命题的逆命题是真命题 （D）假命题的逆命题是假命题 ‎（3）命题“若是偶数，则是偶数”的逆命题是（ ）‎ ‎（A）若是偶数，则是偶数 （B）若是偶数，则是奇数 ‎（C）若是奇数，则是偶数 （D）若是奇数，则是奇数 ‎（4）下列命题正确的是（ ）‎ ‎ （A）三角形的一个外角等于两个内角的和 ‎ （B）三角形的一个外角大于任何一个内角 ‎ （C）有两边和一角对应相等的两个三角报全等 ‎ （D）有两边对应相等的两个直角三角形全等 ‎（5）以下命题的逆命题为真命题的是（ ）‎ ‎（A）三个角相等的三角形是等边三角形 ‎ （B）同角的余角相等 ‎ （C）在三角形中，钝角所对的边最长 ‎ （D）对顶角相等 ‎（6）下列定理中，有逆定理的是（ ）‎ ‎（A）同旁内角互补，两直线平行 （B）直角三角形中没有钝角 ‎（C）互为相反数的数绝对值相等 （D）若，则 参考答案：‎ ‎（1）C （2）A （3）A （4）D （5）A （6）A 填空题 ‎（1）原命题成立，它的逆命题_____成立.‎ ‎（2）一个角的平分线可以看作是________的点的集合.‎ ‎（3）“两条平行线被第三条直线所截，内错角相等”的逆命题是______.‎ ‎（4）“对顶角相等”的逆命题是______，它是_______命题.‎ ‎（5）“有两角和其中一边对应相等的两个三角形全等”的逆命题是________.‎ ‎（6）如图，已知：，，‎ ‎①若，那么N在的_______上.‎ ‎②若M在的角平分线上，那么_______＝_______.‎ 参考答案：‎ ‎（1）不一定 （2）到角的两边的距离相等的所有 （3）如果两条直线被第三条直线所截，内错角相等，那么这两条直线平行 （4）如果两上角相等，那么它们是对顶角；假 （5）两个三角形全等，那么有两角和其中一边对应相等 （6）①角平分线 ②AM；BM 解答题 ‎1．如图，是等腰直角三角形，，BD是的平分线，于E，，求的周长.‎ ‎2．证明题 ‎（1）如图，已知，AD平分，于B，于C，E是AD上一点，‎ 求证：.‎ ‎（2）如图，已知：在中，外角和的平分线BF，CF相交于点F.‎ 求证：点F在的平分线上.‎ ‎（3）如图，已知：BD是的平分线，，点P在BD上，，垂足分别是M、N，‎ 求证：.‎ ‎（4）如图，已知：在中AD是的平分线，于E，于F.‎ 求证：.‎ ‎（5）如图，已知，OM平分，E是OM上一点，过E分别作OP，OQ的垂线，垂足是C，D，且分别交OP，OQ于A，B.‎ 求证：.‎ ‎（6）如图，已知：，于F，于E.‎ 求证：D在的平分线上.‎ 参考答案：‎ ‎1．∵BD是的平分线，∴ ∴.易证， ∴ ∴周长 ‎2． （1）∵AD平分， ∴，可证，∴，而，，∴，∴‎ ‎（2）过点F作，，，垂足为G、H、I.易知，，∴，∴F在的角平分线上.‎ ‎（3）可证，∴，∴.‎ ‎（4）AD是的平分线，∴.∴可证，∴，而∴，，∴，∴，∴.‎ ‎（5）可证，，∴‎ ‎（6）可证，‎ ‎∴‎ ‎∴D在的平分线上.‎ ‎3.9 角的平分线 ‎（一）习题精选 ‎1、判断题 （1） 角的平分线上的点到角的两边的距离相等；‎ （2） 三角形两个内角的平分线交点到三边距离相等；‎ （3） 三角形两个内角的平分线的交点到三个顶点的距离相等；‎ （4） 点E、F分别在∠AOB的两边上，P点到E、F两点距离相等，所以P点在∠AOB的平分线上；‎ （5） 若OC是∠AOB的平分线，过OC上的点P作OC的垂线，交OB于D，交OA于E，则线段PD、PE的长分别是P点到角两边的距离 ‎2、下面说法正确的是（　　）‎ A、每个命题都有逆命题；‎ B、每个定理都有逆定理；‎ C、真命题的逆命题是真命题；‎ D、假命题的逆命题是假命题 ‎3、写出下列定理的逆命题，并判断真假 （1） 同位角相等，两直线平行 （2） 如果，那么 （3） 如果△ABC是直角三角形，那么当△ABC的三个外角中有两个钝角 逆命题是：如果△ABC的三个外角中只有两个是钝角，那么△ABC是直角三角形 （4） 全等的两个三角形的面积相等 提示：任何命题都有逆命题，但定理不一定有逆定理　。‎ ‎4、在△ABC中，∠C＝，BC＝16cm，∠A的平分线AD交BC于D，‎ 且CD：DB＝3：5，则D到AB的距离等于＿＿＿＿‎ 提示：根据题意画出图形，作出表示D到AB距离的线段DE，则有DE＝CD C B 图1‎ A D E ‎5、已知：如图1，BD是∠ABC的平分线，DE⊥AB于E，‎ AB＝18cm,BC＝12cm,求DE的长 提示：由题目条件及图形知 于是要求△BCD中BC边上的高DF，‎ 利用角平分线的性质知道DE＝DF A B C D M 图2‎ ‎6、已知：如图2， ∠B＝∠C＝，M是BC中点，DM平分∠ADC 求证：AM平分∠DAB 提示：要证AM平分∠DAB，‎ 只需证点M在∠DAB的平分线上 因此可考虑运用角平分线的判定定理。‎ A B C E 图3‎ ‎6、已知：如图3，在△ABC中，∠B＝，△ABC的角平分线AD、CE线相交于点O O D 求证：AE+CD＝AC 提示：在AC上截取AF＝AE 由条件不难证得CF＝CD。‎ ‎7、如图，，点E在线段AB上，，‎ 求证：。‎ 分析：结论是，可考虑在AB上截取 AF=AC，只要再证BF=BD即可，这就转化为证明两线 段相等的问题，从而达到简化问题的目的。‎