九年级数学下册第一章直角三角形的边角关系3三角函数的有关计算第2课时课件北师大版 21页

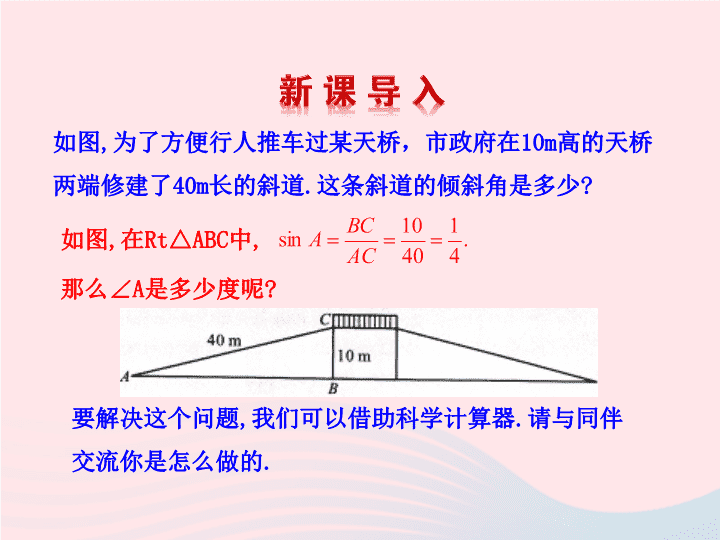
3 三角函数的有关计算 第 2 课时 1 ．经历用计算器由三角函数值求相应锐角的过程，进一步体会三角函数的意义． 2 ．能够利用计算器进行有关三角函数值的计算． 3 ．能够运用计算器辅助解决含三角函数值计算的实际问题． 如图 , 为了方便行人推车过某天桥，市政府在 10m 高的天桥两端修建了 40m 长的斜道 . 这条斜道的倾斜角是多少 ? 那么∠ A 是多少度呢 ? 要解决这个问题 , 我们可以借助科学计算器 . 请与同伴交流你是怎么做的 . 如图 , 在 Rt△ABC 中 , 已知三角函数值求角度,要用到 键 的第二功能 和 键 . 例如 由于计算器的型号与功能不同 , 请按照相应的说明书使用 . sin cos tan 按键顺序 sinA =0.9816 cos A=0.8607 tan A=0.1890 tan A=56.78 2ndf sin 0 . 2ndf cos 0 . 2ndf tan 0 . 2ndf 5 6 . 7 8 9 8 1 sin -1 cos -1 tan -1 2ndf 8 1 6 6 0 7 = 8 9 0 = = = tan 根据下列条件求∠ θ 的大小 : (1)tanθ=2.988 8; (2)sinθ=0.395 7; (3)cosθ=0.785 0; (4)tanθ=0.897 2. 温馨提示:上表的显示结果是以度为单位的,再按 键即可显示以“度 . 分 . 秒”为单位的结果. 2ndf D . M . S 【 跟踪训练 】 （ 2 ） θ ≈23°18′35″ （ 1 ） θ ≈71°30′2″ （ 3 ） θ ≈38°16′46″ （ 4 ） θ ≈41°53′55″ 答案： 例 1. 如图 , 工件上有一 V 形槽 , 测得它的上口宽 20 mm, 深 19.2mm. 求 V 形角 (∠ACB) 的大小 ( 结果精确到 1° ). ∴∠ACD≈27.5° . ∴∠ACB=2∠ACD≈2×27.5° =55°. ∴V 形角约为 55°. 【 例题 】 一辆汽车沿着一山坡行驶了 1000m, 其铅直高度上升了 50m. 求山坡与水平面所成的锐角的大小 . C B A 【 解析 】 在 Rt△ABC 中， 【 跟踪训练 】 例 2. 如图 , 一名患者体内某重要器官后面有一肿瘤 . 在接受放射性治疗时 , 为了最大限度地保证疗效 , 并且防止伤害器官 , 射线必须从侧面照射肿瘤 . 已知肿瘤在皮下 6.3cm 的 A 处 , 射线从肿瘤右侧 9.8cm 的 B 处进入身体 , 求 射线 与皮肤的夹角 . 【 解析 】 如图 , 在 Rt△ABC 中 ,AC=6.3cm,BC=9.8cm, ∴∠B≈32°44′7″. 因此 , 射线与皮肤的夹角约为 32°44′7″. 【 例题 】 1 . 已知sinθ=0.829 04,求锐角θ的大小. 【 解析 】 θ ≈56°0′1″ 【 跟踪训练 】 2 . 一梯子斜靠在一面墙上,已知梯子长4m,梯子位于地面上的一端离墙壁2.5m,求梯子与地面所成的锐角. C B A 【 解析 】 在 Rt△ABC 中， 1.( 广东 · 中考 ) 如图，已知 Rt△ABC 中，斜边 BC 上的高 AD=4 ， cosB= ，则 AC=____________ 。 【 解析 】 因为∠ BAC=90 ° ， AD 是斜边 BC 上的高，所以 ∠ B=∠CAD; 因为 cosB= ，所以在 Rt△ADC 中， cos∠CAD =cosB= , 又因为 AD=4 ，所以 AC=5. 答案： 5 2 ．（重庆 · 中考）已知，如图，在 Rt△ABC 中 ∠ C=90° ， ．点 D 为 BC 边上一点且 BD=2AD ， ∠ ADC=60° 求△ ABC 的周长 . （结果保留根号） 在 Rt△ADC 中 , ∵ ，∴ ∴ 在 Rt △ABC 中 ∴ 的周长为 ∵ ∴ 【 解析 】 , , , , . . . 3 ．（泰州 · 中考）庞亮和李强相约周六去登山，庞亮 从北坡山脚 C 处出发，以 24 米 / 分钟的速度攀登，同时，李 强从南坡山脚 B 处出发．如图，已知小山北坡的坡度 山坡长为 240 米，南坡的坡角是 45° ．问李强以什么速度攀 登才能和庞亮同时到达山顶 A ？（将山路 AB ， AC 看成线段， 结果保留根号） 【 解析 】 过点 A 作 AD⊥BC 于点 D ， 在 Rt△ADC 中，由 得 tanC= ∴∠C=30°∴AD= AC = ×240=120( 米 ). 答：李强以 12 米 / 分钟的速度攀登才能和庞亮同时 到达山顶 A ． 在 Rt△ABD 中，∠ B=45°, 4 ．（嘉兴 · 中考）设计建造一条道路，路基的横断面为梯形 ABCD ，如图（单位：米）．设路基高为 h ，两侧的坡角分别为 α 和 β, 已知 h=2 ， α=45° ， CD=10 ， （ 1 ）求路基底部 AB 的宽 . （ 2 ）修筑这样的路基 1 000 米，需要多少土石方？ 在 Rt△ADE 中，∵ ，∴ 在 Rt△CFB 中，∵ ∴ 在梯形 ABCD 中，又∵ EF ＝ CD ＝ 10 ， ∴ AB ＝ AE ＋ EF ＋ FB ＝ 16 （米）． （ 2 ）在梯形 ABCD 中，∵ AB ＝ 16 ， ∴ 修筑 1 000 米路基，需要土石方： 于点 F ， 于点 E ，则 【 解析 】 （ 1 ）作 ∴ 面积为 （平方米）， 【 规律方法 】 根据题意画出几何图形，构造直角三角形，灵活运用三角函数的定义结合勾股定理的有关知识是进行解题的关键 . 由锐角的三角函数值反求锐角 填表:已知一个角的三角函数值,求这个角的度数(逆向思维) ∠A= ∠A= ∠A= ∠A= ∠A= ∠A= ∠A= ∠A= ∠A= 智慧表现在下一次该怎么做，美德则表现在行为本身 . —— 约尔旦