呼和浩特专版2020中考数学复习方案第三单元函数及其图象第10课时一次函数的图象与性质课件 49页

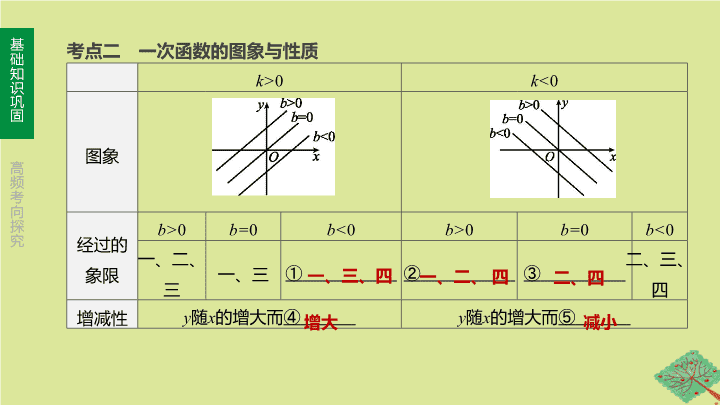
第 10 课时 一次函数的图象与性质 第三单元　函数及其图象 考点一　一次函数的概念 考点聚焦 1 . 一般地 , 形如 y=kx ( k 是常数 , k ≠0) 的函数 , 叫做正比例函数 , 其中 k 叫做比例系数 . 2 . 一般地 , 形如 y=kx + b ( k , b 是常数 , k ≠0) 的函数 , 叫做一次函数 . 当 b= 0 时 , y=kx + b 即 y=kx , 所以说正比例函数是一种特殊的一次函数 . 考点二　一次函数的图象与性质 k> 0 k< 0 图象 经过 的 象限 b> 0 b= 0 b< 0 b> 0 b= 0 b< 0 一、二、 三 一、三 ①   ②   ③   二、三、 四 增减性 y 随 x 的增大 而 ④ 　　　   y 随 x 的增大 而 ⑤ 　　　   一、三、四 一、二、 四 二、四 增大 减小 （续表） b 1 . 方法 : 待定系数法 2 . 步骤 : (1) 设 : 设一般式 y=kx + b ( k ≠0); (2) 列 : 找出直线上两点的坐标 , 分别代入 y=kx + b , 得到关于 k , b 的方程组 ; (3) 解 : 解方程组 , 求得 k , b 的值 ; (4) 依据 k , b 的值 , 写出一次函数的解析式 . 考点三　一次函数的解析式的确定 简记为 “ 左加右减 , 上加下减 ”( 左右平移只给 x 加减 , 上下平移等号右边整体加减 ) 考点四　一次函数图象的平移 考点五　一次函数与一次方程 ( 组 ) 、一元一次不等式的关系 图 10-1 x 0 2 . 一次函数与不等式的关系 (1) 不等式 kx + b> 0( kx + b< 0) 的解集 ⇔ 函数 y=kx + b ( k ≠0) 的图象在 x 轴上方 ( 下方 ) 的部分对应的 x 的取值范围 ⇔ 函数 y=kx + b ( k ≠0) 中 , y ⑩ 　　　　 0 ( y ⑪ 　　　　 0) 时 x 的取值 ;  (2) 如图 10-1, 不等式 k 1 x + b 1 >k 2 x + b 2 的解集是 x>m ; 不等式 k 1 x + b 1 ≤ k 2 x + b 2 的解集是 ⑫ 　　　 .  > < x ≤ m 图 10-1 题组一　必会题 对点演练 1 . 如图 10-2, 直线 l : y= - x -3 与直线 y=a ( a 为常数 ) 的交点在第四象限 , 则 a 的取值范围可能是 ( 　　 ) A . 1 y 2 . 【 方法点析 】 在一次函数 y=kx + b ( k , b 为常数 , k ≠0) 中 , k 和 b 的符号的作用 : ① k 的符号决定增减性 , 当 k> 0 时 , y 随 x 的增大而增大 , 当 k< 0 时 , y 随 x 的增大而减小 ; ② b 的符号决定与 y 轴的交点在 x 轴的上方还是下方 ( 上正、下负 ), 特别地 , 当 b= 0 时 , 函数图象过原点 . | 考向精练 | 1 . 两条直线 y 1 =ax + b 与 y 2 =bx + a 在同一坐标系中的图象可能是下图中的 ( 　　 ) 图 10-4 [ 答案 ]A 　 [ 解析 ] 分四种情况讨论 . 若 a> 0, b> 0, 则直线 y 1 与直线 y 2 均过第一、二、三象限 ; 若 a> 0, b< 0, 则直线 y 1 过第一、三、四象限 , 直线 y 2 过第一、二、四象限 ; 若 a< 0, b> 0, 则直线 y 1 过第一、二、四象限 , 直线 y 2 过第一、三、四象限 ; 若 a< 0, b< 0, 则直线 y 1 与直线 y 2 均过第二、三、四象限 . 故选 A . 2 . [2017· 呼和浩特 6 题 ] 一次函数 y=kx + b 满足 kb> 0, 且 y 随 x 的增大而减小 , 则此函数的图象不经过 ( 　　 ) A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限 [ 答案 ]A 　 [ 解析 ] 由 “ y 随 x 的增大而减小 ” 可知 k< 0, 又由 “ kb> 0” 得 b< 0, 所以图象经过第二、三、四象限 . A 3 . [2016· 呼和浩特 7 题 ] 已知一次函数 y=kx + b - x 的图象与 x 轴的正半轴相交 , 且函数值 y 随自变量 x 的增大而增大 , 则 k , b 的取值情况为 ( 　　 ) A .k> 1, b< 0 B .k> 1, b> 0 C .k> 0, b> 0 D .k> 0, b< 0 考向二　一次函数解析式的确定 解 :(1) ∵图象平行于直线 y= 2 x -1, ∴ k= 2 . 设函数解析式为 y= 2 x + b , 将 (1,3) 代入 , 得 3 = 2×1+ b , ∴ b= 1, ∴ y= 2 x +1 . | 考向精练 | 1 . [2019· 绍兴 ] 若三点 (1,4),(2,7),( a ,10) 在同一直线上 , 则 a 的值等于 ( 　　 ) A . -1 B . 0 C . 3 D . 4 [ 答案 ]C 图 10-5 3 . [2017· 通辽 ] 如图 10-6, 将八个边长为 1 的小正方形摆放在平面直角坐标系中 , 若过原点的直线 l 将图形分成面积相等的两部分 , 则将直线 l 向右平移 3 个单位长度后所得直线 l' 的函数解析式为 　　　　　　 .  图 10-6 考向三　一次函数与方程、不等式组的关系 图 10-7 x= 3 x> 3 x< 3 | 考向精练 | B 2 . [2012· 呼和浩特 7 题 ] 下面四条直线 , 其中直线上每个点的坐标都是二元一次方程 x -2 y= 2 的解的是 ( 　　 ) 图 10-8 C 图 10-9 D 考向四　一次函数与几何综合题 | 考向精练 | 图 10-10 [ 答案 ]A 图 10-11 [ 答案 ] y=x +1 3 . [2018· 呼和浩特一模 ] 矩形 ABCD 中 , AB= 6, BC= 8, 点 P 从点 A 出发沿 A → B → C → D 的路线移动 , 到 D 点停止运动 . 设点 P 移动的路线长为 x ,△ PAD 与矩形 ABCD 不重叠的部分的面积为 y. (1) 写出 y 与 x 之间的函数关系式 . (2) 当 x 取何值时 , y= 28? 并说明此时点 P 在矩形的哪条边上 . 3 . [2018· 呼和浩特一模 ] 矩形 ABCD 中 , AB= 6, BC= 8, 点 P 从点 A 出发沿 A → B → C → D 的路线移动 , 到 D 点停止运动 . 设点 P 移动的路线长为 x ,△ PAD 与矩形 ABCD 不重叠的部分的面积为 y. (2) 当 x 取何值时 , y= 28? 并说明此时点 P 在矩形的哪条边上 . 图 10-12 图 10-12 图 10-12