2010中考数学中山考试试题 8页

‎2010年广东省中山市初中毕业生学业考试 数 学 试 题 说明：1．全卷共6页，考试用时100分钟，满分为120分。‎ ‎2．答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、试室号、座位号。用2B铅笔把对应该号码的标号涂黑。‎ ‎3．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试题上。‎ ‎4．非选择题必须用黑色字迹钢笔或签字笔作答、答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。不按以上要求作答的答案无效。‎ ‎5．考生务必保持答题卡的整洁。考试结束时，将试卷和答题卡一并交回。‎ 一、选择题（本大题5小题，每小题3分，共15分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑。‎ 第2题图 B C E D A ‎1‎ ‎1．－3的相反数是（　　）‎ A．3 　 B．　 C．－3　 D．‎ ‎2．如图，已知∠1 = 70º，如果CD∥BE，那么∠B的度数为（　　）‎ A．70º　 B．100º 　C．110º D．120º ‎ ‎3．某学习小组7位同学，为玉树地震灾区捐款，捐款金额分别为5元，10元，6元，6元，7元，‎ ‎8元，9元，则这组数据的中位数与众数分别为（　　）‎ A．6，6　 B．7，6 　C．7，8 D．6，8‎ ‎4．左下图为主视方向的几何体，它的俯视图是（　　）‎ A．‎ B．‎ D．‎ C．‎ 主视方向 第4题图 ‎5．下列式子运算正确的是（　　）‎ A． B．　 C．　 D．‎ 二、填空题（本大题5小题，每小题4分，共20分）‎ 请将下列各题的正确答案填写在答题卡相应的位置上。‎ ‎6． 据中新网上海6月1日电：世博会开园一个月来，客流平稳，累计至当晚19时，参观者已超过8000000‎ 人次。试用科学记数法表示8000000=_______________________。‎ ‎7．化简：=_______________________。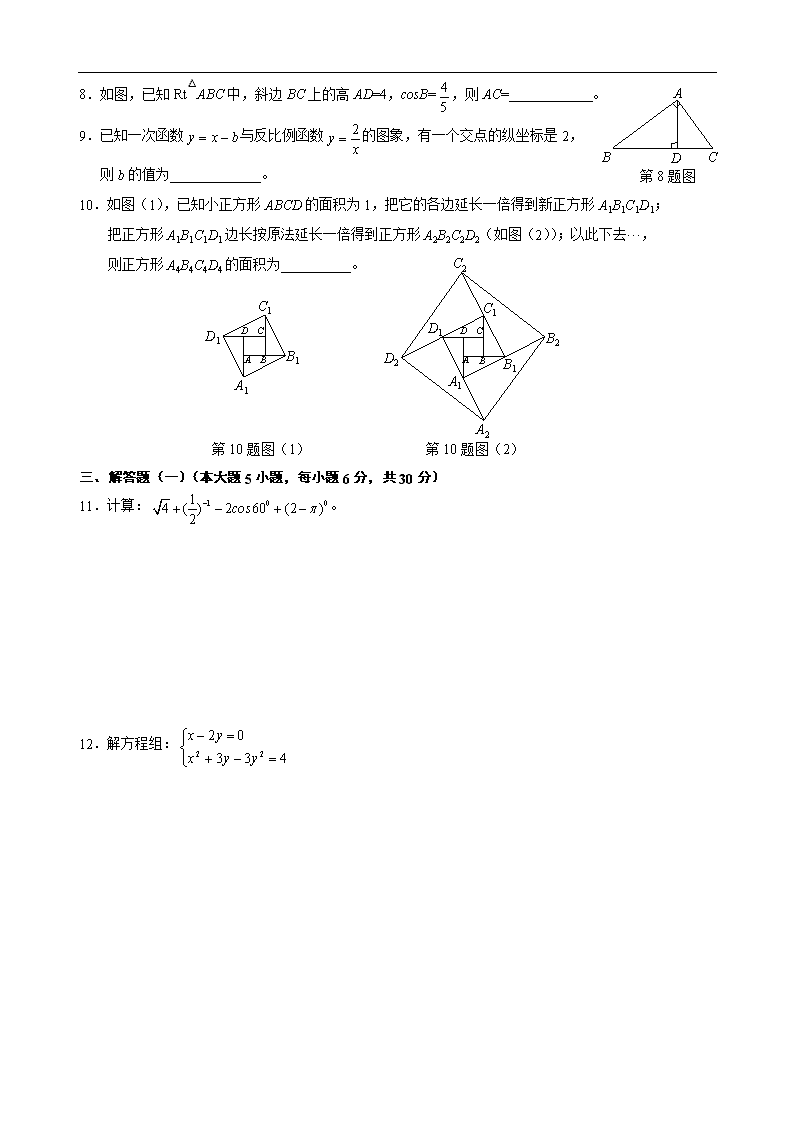‎ 第8题图 A B C D ‎8．如图，已知Rt△ABC中，斜边BC上的高AD=4，cosB=，则AC=____________。‎ ‎9．已知一次函数与反比例函数的图象，有一个交点的纵坐标是2，‎ 则b的值为_____________。‎ ‎10．如图（1），已知小正方形ABCD的面积为1，把它的各边延长一倍得到新正方形A1B1C1D1；‎ 把正方形A1B‎1C1D1边长按原法延长一倍得到正方形A2B‎2C2D2（如图（2））；以此下去···，‎ 第10题图（1）‎ A1‎ B1‎ C1‎ D1‎ A B C D D2‎ A2‎ B2‎ C2‎ D1‎ C1‎ B1‎ A1‎ A B C D 第10题图（2）‎ 则正方形A4B‎4C4D4的面积为__________。‎ 三、解答题（一）（本大题5小题，每小题6分，共30分）‎ ‎11．计算：。‎ ‎12．解方程组：‎ ‎13．如图，方格纸中的每个小方格都是边长为1个单位的正方形，Rt△ABC的顶点均在格点上，在建立平面直角坐标系后，点A的坐标为（－6，1），点B的坐标为（－3，1），点C的坐标为（－3，3）。‎ ‎（1）将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1，试在图上画出的图形Rt△A1B1C1的图形，‎ 并写出点A1的坐标；‎ ‎（2）将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A2B2C2，试在图上画出Rt△A2B2C2的图形。‎ 第13题图 A x y B C ‎1‎ ‎1‎ ‎-1‎ O ‎14．如图，PA与⊙O相切于A点，弦AB⊥OP，垂足为C，OP与⊙O相交于D点，已知OA=2，OP=4。‎ ‎（1）求∠POA的度数；‎ 第14题图 C B P D A O ‎（2）计算弦AB的长。‎ ‎15．已知一元二次方程。‎ ‎（1）若方程有两个实数根，求m的范围；‎ ‎（2）若方程的两个实数根为x1，x2，且，求m的值。‎ 四、解答题（二）（本大题4小题，每小题7分，共28分）‎ ‎16．分别把带有指针的圆形转盘A、B分成4等份、3等份的扇形区域，并在每一小区域内标上数字（如图所示）。欢欢、乐乐两人玩转盘游戏，游戏规则是：同时转动两个转盘，当转盘停止时，若指针所指两区域的数字之积为奇数，则欢欢胜；若指针所指两区域的数字之积为偶数，则乐乐胜；若有指针落在分割线上，则无效，需重新转动转盘。‎ 第16题图 ‎1‎ ‎2‎ ‎1‎ ‎2‎ ‎3‎ ‎3‎ ‎5‎ 转盘A 转盘B ‎（1）试用列表或画树状图的方法，求欢欢获胜的概率；‎ ‎（2）请问这个游戏规则对欢欢、乐乐双方公平吗？试说明理由。‎ 第17题图 O ‎3‎ ‎－1‎ x y ‎17．已知二次函数的图象如图所示，它与x轴的一个交点坐标为（－1，0），‎ 与y轴的交点坐标为（0，3）。‎ ‎（1）求出b，c的值，并写出此二次函数的解析式；‎ ‎（2）根据图象，写出函数值y为正数时，自变量x的取值范围。‎ A B C D E F 第18题图 ‎18．如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE。已知∠BAC=30º，‎ EF⊥AB，垂足为F，连结DF。‎ ‎（1）试说明AC=EF；‎ ‎（2）求证：四边形ADFE是平行四边形。‎ ‎19．某学校组织340名师生进行长途考察活动，带有行李170件，计划租用甲、乙两种型号的汽车 ‎10辆。经了解，甲车每辆最多能载40人和16件行李，乙车每辆最多能载30人和20件行李。‎ ‎（1）请你帮助学校设计所有可行的租车方案；‎ ‎（2）如果甲车的租金为每辆2000元，乙车的租金为每辆1800元，问哪种可行方案使租车费用最省？‎ 五、解答题（三）（本大题3小题，每小题9分，共27分）‎ ‎20．已知两个全等的直角三角形纸片ABC、DEF，如图（1）放置，点B、D重合，点F在BC上，AB与EF交于点G。∠C=∠EFB=90º，∠E=∠ABC=30º，AB=DE=4。‎ ‎（1）求证：△EGB是等腰三角形；‎ 第20题图（1）‎ A B C E F F B（D）‎ G G A C E D 第20题图（2）‎ ‎（2）若纸片DEF不动，问△ABC绕点F逆时针旋转最小_____度时，四边形ACDE成为以ED为底的梯形（如图（2）），求此梯形的高。‎ ‎21．阅读下列材料：‎ ‎1×2 = ×(1×2×3－0×1×2)，‎ ‎2×3 = ×(2×3×4－1×2×3)，‎ ‎3×4 = ×(3×4×5－2×3×4)，‎ 由以上三个等式相加，可得 ‎1×2＋2×3＋3×4 = ×3×4×5 = 20。‎ 读完以上材料，请你计算下列各题：‎ (1) ‎1×2＋2×3＋3×4＋···＋10×11（写出过程）；‎ (2) ‎1×2＋2×3＋3×4＋···＋n×(n＋1) = _________；‎ (3) ‎1×2×3＋2×3×4＋3×4×5＋···＋7×8×9 = _________。‎ ‎22．如图（1），（2）所示，矩形ABCD的边长AB=6，BC=4，点F在DC上，DF=2。动点M、N分别 从点D、B同时出发，沿射线DA、线段BA向点A的方向运动（点M可运动到DA的延长线上），‎ 当动点N运动到点A时，M、N两点同时停止运动。连接FM、FN，当F、N、M不在同一直线时，‎ 可得△FMN，过△FMN三边的中点作△PQW。设动点M、N的速度都是1个单位/秒，M、N运动的 时间为x秒。试解答下列问题：‎ ‎（1）说明△FMN∽△QWP；‎ ‎（2）设0≤x≤4（即M从D到A运动的时间段）。试问x为何值时，△PQW为直角三角形？‎ 当x在何范围时，△PQW不为直角三角形？‎ 第22题图（2）‎ A B C D F M N W P Q ‎（3）问当x为何值时，线段MN最短？求此时MN的值。‎ 第22题图（1）‎ A B M C F D N W P Q ‎2010年广东省中山市初中毕业生学业考试 数 学 试 题 参 考 答 案 ‎1、A 2、C 3、B 4、D 5、D ‎ ‎6、 7、 8、5 9、 10、625 ‎ 第13题（1）答案 A x y B C ‎1‎ ‎1‎ ‎-1‎ O A1‎ B1‎ C1‎ ‎11、解：原式。‎ ‎…………… ①‎ ‎…… ②‎ ‎12、解： ‎ ‎ 由①得： ………… ③ ‎ 将③代入②，化简整理，得：‎ ‎ ‎ 第13题（2）答案 A x y B C ‎1‎ ‎1‎ ‎-1‎ O A2‎ B2‎ C2‎ 解得：‎ ‎ ‎ ‎ 将代入①，得：‎ ‎ 或 ‎13、（1）如右图，A1（-1，1）； （2）如右图。‎ ‎14、（1）60° （2）‎ ‎15、（1）m≤1 （2）‎ ‎16、（1） （2）不公平。因为欢欢获胜的概率是；乐乐获胜的概率是。‎ ‎17、（1） （2）‎ ‎18、（1）提示： ‎ ‎（2）提示：，AD∥EF且AD=EF ‎19、（1）四种方案，分别为： ‎ ‎（2） 最便宜，费用为18800元。‎ ‎20、（1）提示： （2）30（度）‎ ‎21、（1）原式 （2） （3）1260‎ ‎22、（1）提示：∵PQ∥FN，PW∥MN ∴∠QPW =∠PWF，∠PWF =∠MNF ∴∠QPW =∠MNF ‎ 同理可得：∠PQW =∠NFM或∠PWQ =∠NFM ∴△FMN∽△QWP ‎ ‎（2）当时，△PQW为直角三角形；‎ 当0≤x<，