人教版九年级数学下册第二十六章《反比例函数》 单元同步检测试题（含答案） 9页

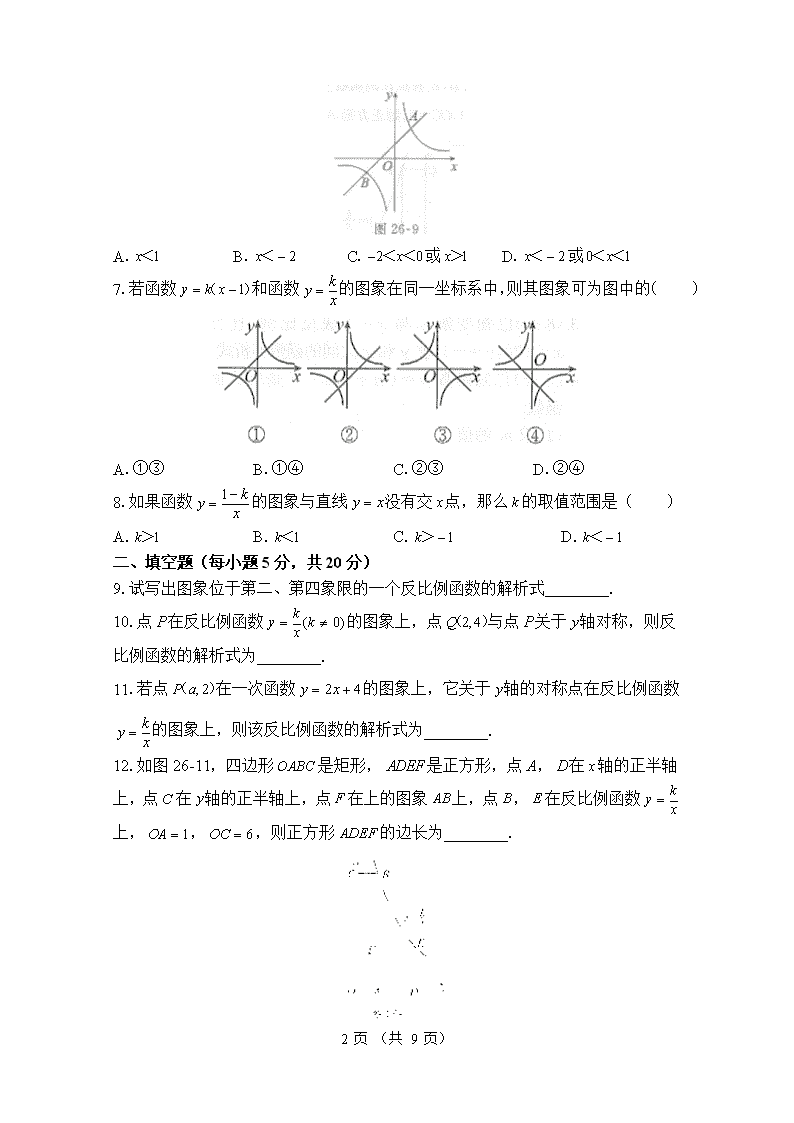
第二十六章《反比例函数》单元检测题题号一二三总分2122232425262728分数一、选择题（每小题4分，共32分）1.下列函数是反比例函数的是（）A.B.C.D.2.当时，函数的图x象在（）A.第四象限B.第三象限C.第二象限D.第一象限3.反比例函数的图象经过点，则的值为（）A.6B.C.D.4.已知反比例函数，下列结论不正确的是（）A.图象经过点B.图象在第一、第三象限C.当时，D.当时，随的增大而增大5.在一个可以改变体积的密闭容器内装有一定质量的二氧化碳，当改变容器的体积时，二氧化碳的密度也会随之改变，密度（单位：）是体积（单位：）的反比例函数，它的图象如图26-8所示，当时，二氧化碳的密度是（）A.B.C.D.6.如图26-9，一次函数的图象和反比例函数的图象交于，两点，若，则的取值范围是（）9页（共9页） A.B.C.或D.或7.若函数和函数的图象在同一坐标系中，则其图象可为图中的（）A.①③B.①④C.②③D.②④8.如果函数的图象与直线没有交点，那么的取值范围是（）A.B.C.D.二、填空题（每小题5分，共20分）9.试写出图象位于第二、第四象限的一个反比例函数的解析式________.10.点在反比例函数的图象上，点与点关于轴对称，则反比例函数的解析式为________.11.若点在一次函数的图象上，它关于轴的对称点在反比例函数的图象上，则该反比例函数的解析式为________.12.如图26-11，四边形是矩形，是正方形，点，在轴的正半轴上，点在轴的正半轴上，点在上的图象上，点，在反比例函数上，，，则正方形的边长为________.9页（共9页） 三、解答题（共48分）13.（8分）已知变量与成反比例，且当时，，求和之间的函数解析式。14.（8分）已知函数是反比例函数.（1）求的值；（2）此反比例函数随的增大如何变化？15.（10分）图26-12是某一蓄水池每小时的排水量（单位：）与排完水池中的水所用的时间（单位：）之间的函数关系图象。（1）请你根据图象提供的信息求出此函数的解析式；（2）如果要6h排完水池中的水，那么每小时的排水量应该是多少？16.（10分）如图26-13，在平面直角坐标系中，反比例函数的图象和矩形在第一象限，平行于轴，且，，点的坐标为.9页（共9页） （1）直接写出，，三点的坐标；（2）若将矩形向下平移，矩形的两个顶点恰好同时落在反比例函数的图象上，猜想这是哪两个点，并求矩形的平移距离和反比例函数的解析式.17.（12分）如图26-14，一次函数（为常数，且）的图象与反比例函数的图象交于，两点.（1）求一次函数的解析式；（2）若将直线向下平移个单位长度后与反比例函数的图象有且只有一个公共点，求的值.9页（共9页） 第二十六章综合测试答案解析一、1.【答案】B【解析】根据反比例函数的定义，可化为形如的函数即为反比例函数.2.【答案】A【解析】因为函数中，所以其图象位于第二、第四象限，当时，其图象位于第四象限.3.【答案】C【解析】把点代入反比例函数中，得，解得.4.【答案】D【解析】当时，随的增大而减小.5.【答案】D【解析】根据题意，密度与体积成反比例函数，且过点，故.故当时，二氧化碳的密度.6.【答案】D【解析】因为当一次函数图象位于反比例函数图象的下方时，所以或.7.【答案】C【解析】因为只能取正数或负数，所以可分和讨论求解。当时，一次函数的图象经过第一、三、四象限，反比例函数的图象在第一、三象限，故选②；当时，一次函数的图象经过第一、二、四象限，反比例函数的图象在第二、四象限，故选③.8.【答案】A【解析】函数的图象与直线没有交点，则函数的图象一定在第二、第四象限，此时，解得.二、9页（共9页） 9.【答案】（答案不唯一）【解析】位于第二、第四象限的反比例函数的比例系数.10.【答案】【解析】因为点和点关于轴对称，所以点的坐标为.将代入解析式，得，故反比例函数的解析式为.11.【答案】【解析】因为点在一次函数的图象上，所以，解得，所以点的坐标为.所以点关于轴对称的点的坐标为.故过点的反比例函数的解析式为.12.【答案】2【解析】由题意，得，即，解得（负值舍去）三、13.【答案】解：设反比例函数的解析式为.因为当时，，所以，解得.故.【解析】设出反比例函数的解析式，利用待定系数法求解。14.【答案】解：（1）因为函数为反比例函数，所以，解得.9页（共9页） （2）由（1），得反比例函数的解析式为因为，所以反比例函数在每个象限内随的增大而减小.【解析】（1）根据反比例函数的系数不为0和次数为，求；（2）根据比例系数的符号判断性质.15.【答案】解：（1）由题中图象可知，与成反比例函数关系，设，代入点可得，则与之间的函数解析式为.（2）当时，，即如果要排完水池中的水，那么每小时的排水量应该是.【解析】（1）设，依据题中图象上点的坐标，可以求得与之间的函数解析式；（2）求当时，的值.16.【答案】解：（1），，.（2）这两个点是，，如答图26-1所示，矩形平移后得到矩形.设平移距离为，则，，因为点，在的图象上，所以，解得，所以点，所以矩形的平移距离为3，反比例函数的解析式为【解析】（1）与点、点与点的横坐标相等，点与点、点与点的纵坐标相等，再根据，的长即可求出，，三点的坐标。（2）根据矩形的位置及反比例函数图象的特点，可猜得这两个点为，，可设平移的距离为，再根据反比例函数图象上的点的横、纵坐标的积相等，列出方程，求出的值，得到反比例函数的解析式。9页（共9页） 17.【答案】解：（1）由题意，得，解得，所以一次函数的解析式为.（2）直线向下平移个单位长度后，解析式为，整理，得.所以，解得或.9页（共9页） 9页（共9页）