中考数学复习冲刺专项训练精讲：勾股定理与解直角三角形的简单应用教学课件 11页

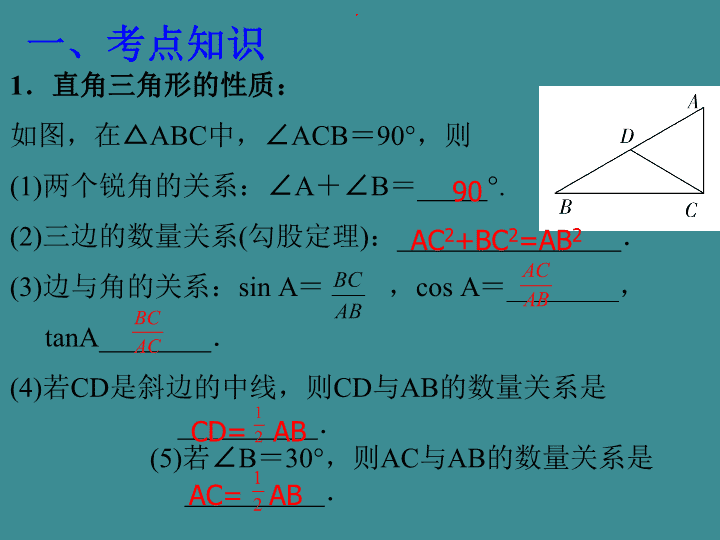
第四章三角形勾股定理与解直角三角形的简单应用中考数学复习冲刺专项训练精讲 1．直角三角形的性质：如图，在△ABC中，∠ACB＝90°，则(1)两个锐角的关系：∠A＋∠B＝_____°.(2)三边的数量关系(勾股定理)：________________．(3)边与角的关系：sinA＝，cosA＝________，tanA________．(4)若CD是斜边的中线，则CD与AB的数量关系是__________．(5)若∠B＝30°，则AC与AB的数量关系是__________．一、考点知识，90CD=ABAC2+BC2=AB2AC=AB 3．在Rt△ABC中，∠ACB＝90°，CD是斜边AB上的高，S△ABC＝AC×________＝AB×________．2．直角三角形的判定：(1)定义法：当∠ACB＝______°时，△ABC是直角三角形．(2)勾股定理的逆定理：当△ABC的三边满足____________时，△ABC是直角三角形，且∠ACB＝90°.(3)CD是AB边上的中线，且__________________时，△ABC是直角三角形，且斜边是________．90AC2+BC2=AB2CD=ABABBCCD 【例1】如图，在菱形ABCD中，对角线AC与BD相交于点O，AC＝8，BD＝6，OE⊥BC，垂足为点E，求OE的长．【考点1】勾股定理，等面积法二、例题与变式解：∵菱形的对角线互相垂直平分，∴OB＝3，OC＝4，∠BOC＝90°.∴BC＝.∵S△OBC＝OB·OC＝BC·OE.∴OB·OC＝BC·OE，即3×4＝5OE.∴OE＝. 【考点2】直角三角形边与角的关系【例2】如图，在△ABC中，BD⊥AC，AB＝6，AC＝，∠A＝30°.(1)求BD和AD的长；(2)求tanC的值．解：（1）∵BD⊥AC，∴∠ADB=90°.在Rt△ADB中，AB=6，∠A=30°，∴BD=AB=3.∴AD=BD=.（2）CD=AC－AD=，在Rt△ADC中，tan∠C=. 【变式2】如图，在Rt△ABC中，∠C＝90°，∠A＝30°，点E为线段AB上的一点，且AE∶EB＝4∶1，EF⊥AC于点F，连接FB，求tan∠CFB.解：在Rt△ABC中，∠C=90°，∠A=30°，设BC=x，则AB=2x，AC=x.又∵EF⊥AC，∴EF∥BC.∴AF∶FC=AE∶EB=4∶1,CF=AC=.∴在Rt△CFB中,∴tan∠CFB=. 【考点3】直角三角形的性质【例3】如图，在△ABC中，∠C＝90°，BD平分∠ABC，若AC＝12cm，DC＝5cm，求sinA的值．解：过点D作DE⊥AB于点E，∵BD是∠ABC的平分线，∠C=90°，DE⊥AB，∴DE=CD=5cm，∵AD=12－5=7cm，∴SinA=. 【变式3】如图，OP平分∠AOB，∠AOP＝15°，PC∥OA，PD⊥OA于点D，PC＝4，求PD的长．解：过点P作PE⊥OB于E，∵∠AOP=∠BOP，PE⊥OB，PD⊥OA，∴PE=PD.∠BOP=∠AOP=15°，∴∠AOB=30°.∵PC∥OA，∴∠BCP=∠AOB=30°.∴在Rt△PCE中，PE=PC=×4=2.∴PD=PE=2. 1．如图，P是⊙O外一点，PA是⊙O的切线，PO＝13，PA＝12，求sinP的值．解：连接OA,∵PA是⊙O的切线，∴OA⊥AP，即∠OAP=90°．又∵PO=13，PA=12，∴根据勾股定理，得OA=.∴sinP=.A组 B组2．如图，在矩形ABCD中，对角线AC，BD相交于点O，点E，F分别是AO，AD的中点，若AB＝6cm，BC＝8cm，求EF的长．解：∵四边形ABCD是矩形，∴∠ABC=90°，BD=AC，BO=OD=BD，∵AB=6cm，BC=8cm，∴由勾股定理,得BD=AC=（cm），∴DO=5cm，∵点E,F分别是AO,AD的中点，∴EF=OD=2.5cm C组3．如图，在四边形ABCD中，∠ABC＝90°，AB＝3，BC＝4，CD＝10，DA＝，求BD的长．解：连接AC，过点D作BC边上的高，交BC延长线于点H．在Rt△ABC中，AB＝3，BC＝4，∴AC＝5.又CD＝10，DA＝，可知△ACD为直角三角形，且∠ACD＝90°.易证△ABC∽△CHD，相似比为，则CH＝6，DH＝8.∴BD＝.