苏科版九年级上期中质量调研检测数学试卷（苏教版九年级数学上册期中考试测试卷） 5页

苏教版九年级数学上册期中考试测试卷一、选择题（本大题共6小题，每小题2分，共12分）1．已知OA=4cm，以O为圆心，r为半径作⊙O．若使点A在⊙O内，则r的值可以是（　　）　A.2cmB.3cmC.4cmD.5cm2．一元二次方程(x－1)2=1－x的根为（　　）　A0B．1C．－1或0D．1或03．某商场试销一种新款衬衫，一周内销售情况如下表所示：型号（厘米）383940414243数量（件）25303650288商场经理要了解哪种型号最畅销，则上述数据的统计量中，对商场经理来说最有意义的是（　　）．A．平均数B．众数C．中位数D．方差4．同时掷两枚质地均匀的硬币，出现结果都是“正面朝上”的概率为（　　）．A．B．C．D．5．下列关于x的一元二次方程中，有两个相等实数根的方程是（　　）A．x2＋1=0B．x2－1=0C．x2－2x＋1=0D．x2－2x－1=06．如图，AB是⊙O的直径，CD是⊙O的切线，切点为D，CD与AB的延长线交于点C，∠A=30°，给出下面3个结论：①AD=CD；②BD=BC；③AB=2BC．AOD其中，正确结论的个数为（　　）CA．3个B．2个C．1个D．0个(第6题)二、填空题（本大题共10小题，每小题2分，共20分）7．某公司欲招聘一名公关人员，对甲、乙两位候选人进行了面试和笔试，他们的成绩如表：候选人甲乙测试成绩（百分制）面试8692笔试9083如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权．根据两人的平均成绩，公司将录取．8．代数式x2＋4x＋1化为（x＋m）2＋n的形式（其中m、n为常数）是． 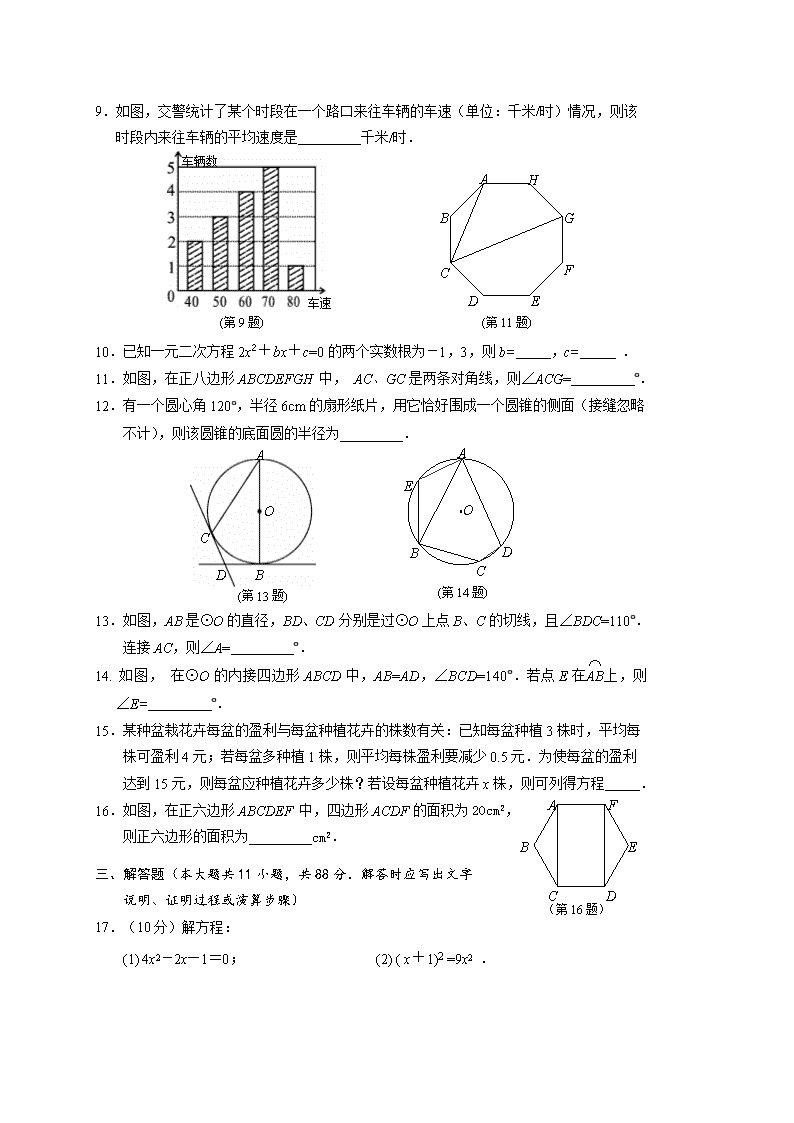9．如图，交警统计了某个时段在一个路口来往车辆的车速（单位：千米/时）情况，则该时段内来往车辆的平均速度是千米/时．ADEFGH车辆数BC车速(第11题)(第9题)10．已知一元二次方程2x2＋bx＋c=0的两个实数根为－1，3，则b=，c=．11．如图，在正八边形ABCDEFGH中，AC、GC是两条对角线，则∠ACG=°．12．有一个圆心角120°，半径6cm的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略AABCDE(第14题)O不计），则该圆锥的底面圆的半径为．OCBD(第13题)13．如图，AB是⊙O的直径，BD、CD分别是过⊙O上点B、C的切线，且∠BDC=110°．连接AC，则∠A=°．14.如图，在⊙O的内接四边形ABCD中，AB=AD，∠BCD=140°．若点E在上，则∠E=°．15．某种盆栽花卉每盆的盈利与每盆种植花卉的株数有关：已知每盆种植3株时，平均每株可盈利4元；若每盆多种植1株，则平均每株盈利要减少0.5元．为使每盆的盈利达ABCDFE（第16题）到15元，则每盆应种植花卉多少株？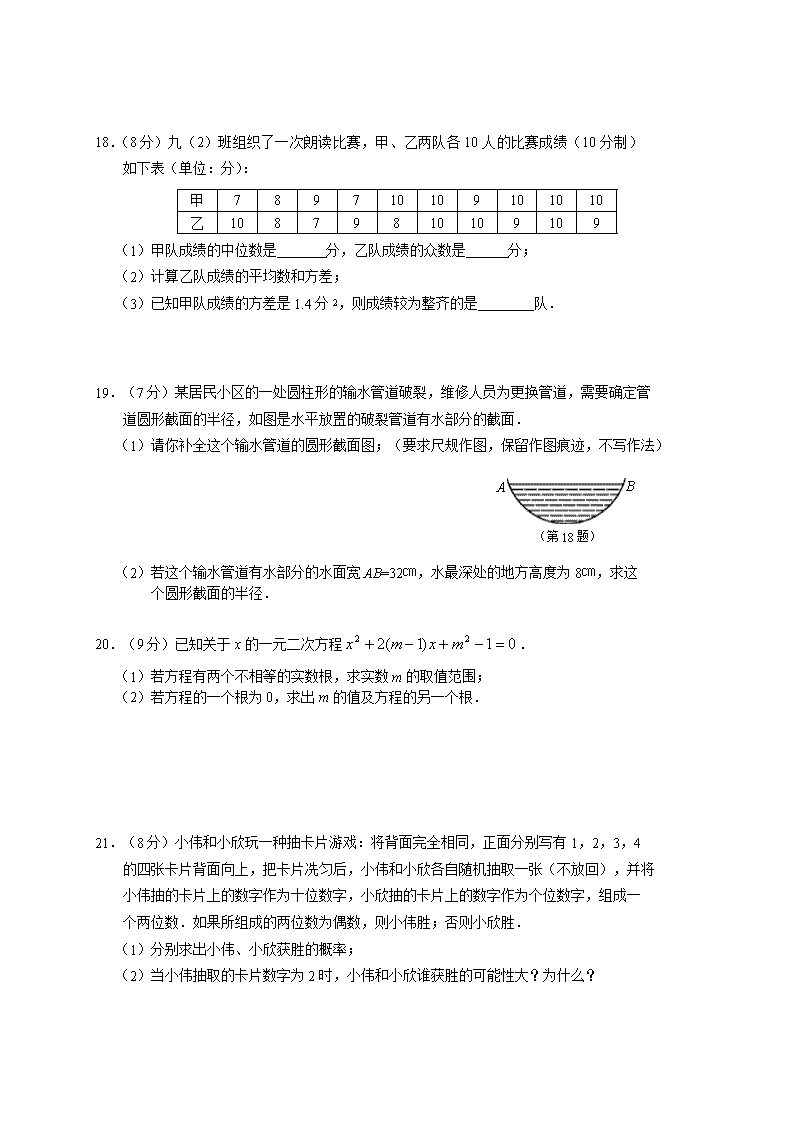若设每盆种植花卉x株，则可列得方程．16．如图，在正六边形ABCDEF中，四边形ACDF的面积为20cm2，则正六边形的面积为cm2．三、解答题（本大题共11小题，共88分．解答时应写出文字说明、证明过程或演算步骤）17．（10分）解方程：(1)4x2－2x—1＝0；(2)(x＋1)2=9x2． 18．（8分）九（2）班组织了一次朗读比赛，甲、乙两队各10人的比赛成绩（10分制）如下表（单位：分）：甲789710109101010乙10879810109109（1）甲队成绩的中位数是　分，乙队成绩的众数是　分；（2）计算乙队成绩的平均数和方差；（3）已知甲队成绩的方差是1.4分2，则成绩较为整齐的是　　队．19．（7分）某居民小区的一处圆柱形的输水管道破裂，维修人员为更换管道，需要确定管道圆形截面的半径，如图是水平放置的破裂管道有水部分的截面．（1）请你补全这个输水管道的圆形截面图；（要求尺规作图，保留作图痕迹，不写作法）BA（第18题）（2）若这个输水管道有水部分的水面宽AB=32㎝，水最深处的地方高度为8㎝，求这个圆形截面的半径．20．（9分）已知关于x的一元二次方程．（1）若方程有两个不相等的实数根，求实数m的取值范围；（2）若方程的一个根为0，求出m的值及方程的另一个根．21．（8分）小伟和小欣玩一种抽卡片游戏：将背面完全相同，正面分别写有1，2，3，4的四张卡片背面向上，把卡片冼匀后，小伟和小欣各自随机抽取一张（不放回），并将小伟抽的卡片上的数字作为十位数字，小欣抽的卡片上的数字作为个位数字，组成一个两位数．如果所组成的两位数为偶数，则小伟胜；否则小欣胜．（1）分别求出小伟、小欣获胜的概率；（2）当小伟抽取的卡片数字为2时，小伟和小欣谁获胜的可能性大？为什么？ 22．（7分）如图，⊙O是△ABC的外接圆，AB＝AC，P是⊙O上一点．（1）请你只用无刻度的直尺，分别画出图1和图2中∠P的平分线；AOBCOABCP（2）结合图2，说明你这样画的理由．P图2图1（第22题）AOCEDB(第23题)23．（8分）如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，E为BC的中点，连接DE．（1）求证：DE是⊙O的切线；[中@国%教#（2）若AC=BC，判断四边形OCED的形状，并说明理由．24．（9分）如图，点B、C、D都在⊙O上，过点C的⊙O的切线交OB延长线于点A，C连接CD、BD，若∠CDB=∠OBD=30°，OB=6cm．（1）求证：AC∥BD；（2）求由弦CD、BD与弧BC所围成的阴影O部分的面积．（结果保留π）(第24题)25．（9分）如图，某市近郊有一块长为60米，宽为50米的矩形荒地，地方政府准备在此 建一个综合性休闲广场，其中阴影部分为通道，通道的宽度均相等，中间的三个矩形（其中三个矩形的一边长均为a米）区域将铺设塑胶地面作为运动场地．设通道的宽度为x米．（1）a＝（用含x的代数式表示）；（2）若塑胶运动场地总占地面积为2430平方米，则通道的宽度为多少米？aaa(第25题)60米50米26．（13分）（1）如图1，AB为⊙O的弦，D为AB上一点，且OD⊥OB．直线l与⊙Ol图1相切与点A，且直线l与OD的延长线交于点C．①求证：AC=CD；②若AC=2，OA=，求线段OD的长．（2）如图2，AB为⊙O的弦，D为AB上一点，且OD⊥OB．直线⊥OA，且直线与OA的延长线交于点A’，与BA的延长线交于点E，与OD的延长线相交于点C’．①在图2中找出与C’D相等的线段，并说明理由；②若A’C’=9cm，OA’=12cm，⊙O的半径为6cm，求线段OD的长.A’C’图2