中考数学专题复习练习：垂直于弦的直径1 5页

垂直弦的直径 一、圆是轴对称（有无数条对称轴，过圆心的任一条直线都是对称轴）；又是中心对称，对称中心是圆心.‎ C D A B O E 二、垂径定理 垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧.‎ ‎ 符号语言：∵CD为⊙O的直径，AB为⊙O的弦，且CD⊥AB，垂足为E，‎ ‎∴ AE=BE, = , = .‎ 推 论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧.‎ ‎∵ CD为⊙O的直径，AB为⊙O的弦（不是直径），且AE=BE.‎ ‎∴ CD⊥AB， = , = .‎ 弦心距：圆心到弦的距离（垂线段OE）‎ 考点分析：‎ 垂径定理及推论的应用，证明.‎ 典型例题分析 类型1. 垂径定理及推论概念 例1．下面四个命题中正确的一个是（ ）‎ A．平分一条直径的弦必垂直于这条直径 B．平分一条弧的直线垂直于这条弧所对的弦 C．弦的垂线必过这条弦所在圆的圆心 D．在一个圆内平分一条弧和它所对弦的直线必过这个圆的圆心 例2. 如图1-2，如果为⊙直径，弦，垂足为，‎ 那么下列结论中错误的是（ ）‎ A． B． C． D．‎ 例3. 如图1－3在⊙O中，弦CD垂直平分半径OA，且CD＝‎6cm， ‎ 则半径OA的长为（ ）‎ ‎ A. B. C. D. ‎ C ‎ A ‎ D ‎ O ‎ ‎ 图1－2 图1－3 图1－4‎ 例4. 如图1－4，⊙O的直径CD与弦AB交于点M，添加条件：_____________（写出一个即可），就可得到M是AB的中点.类型2. 垂径定理的运用在垂径定理的运用中，通常的是要利用定理构建直角三角形，利用勾股定理进行运算.‎ 例5. 过⊙内一点的最长的弦长为，最短的弦长为，那么⊙的半径等于________，的长为________‎ 类型2. 垂径定理分类讨论 例1. 如图2－1，⊙O的直径为10，弦AB的长为8，M是弦AB上的动点，‎ 则OM的长的取值范围是（ ）‎ A. B. C. D. 图2－1 ‎ 例2. 已知：AB、CD为⊙O的两条弦，且AB∥CD，⊙O的半径为‎5cm，AB=‎8cm，CD=‎6cm，求AB、CD之间的距离.‎ 例3. 已知：△ABC内接于⊙O，AB=AC，半径OB=‎5cm，圆心O到BC的距离为‎3cm，求AB的长．‎ 类型3. 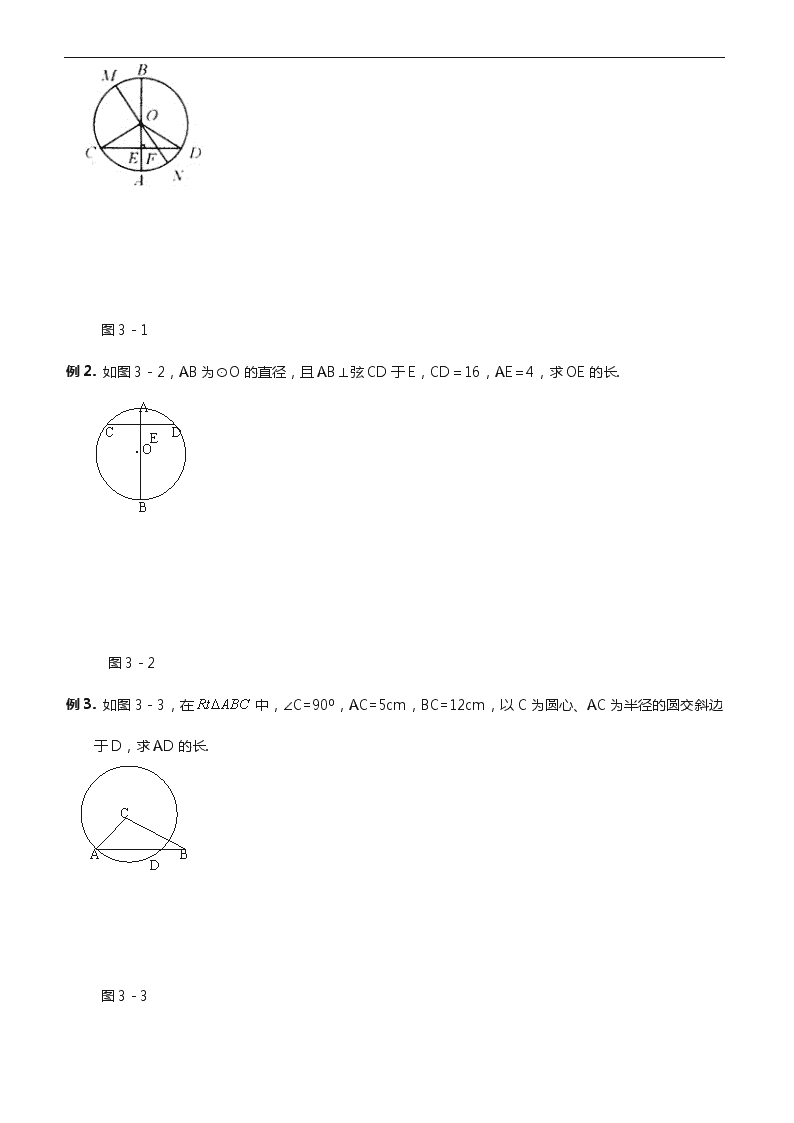利用垂径定理求线段长度，角度 例1. 如图3－1，在圆中，直径垂直于弦，并且交于，直径交于，且，求.‎ ‎ ‎ ‎ 图3－1‎ 例2. 如图3－2，AB为⊙O的直径，且AB⊥弦CD于E，CD＝16，AE＝4，求OE的长.‎ A C B C D ‎ CCC E ‎ ‎.O ‎ ‎ 图3－2‎ 例3. 如图3－3，在中，∠C=900，AC=‎5cm，BC=‎12cm，以C为圆心、AC为半径的圆交斜边于D，求AD的长.‎ A ‎ C ‎ B ‎ D ‎ 图3－3‎ 例4. 如图3－4，已知：AB是⊙O的直径，弦CD交AB于E点，BE＝1，AE＝5，∠AEC＝300，‎ 求CD的长.‎ B ‎ D ‎ C ‎ B ‎ A ‎ ‎.O ‎ ‎ 图3－4‎ 例5. 如图3－5，O是两个同心圆的圆心，大圆的弦AB交小圆于C、D两点，OE⊥CD于E，若AB=2CD=4OE ‎ 求：大圆半径R与小圆半径r之比.‎ A ‎ C ‎ O ‎ E ‎ D ‎ B ‎ ‎ 图3－5‎ 类型4. 垂径定理相关证明 例1.如图4－1，，是⊙的直径，．求证：．‎ ‎ 图4－1‎ 例2．如图4－2，F是以O为圆心，BC为直径的半圆上任一点，A是 的中点，AD⊥BC于D.‎ 求证：‎ 图4－2‎ 例3．已知：如图4－3，⊙的弦，相交于点，是的平分线，点,分别是， 的中点，分别交，于点，．求证：．‎ ‎ 图4－3‎ 例4．如图，⊙的直径和弦相交于点，，，垂足分别是，．‎ ‎(1)求证：．‎ ‎(2)若，，求的值．‎ 图4－4‎ 类型5. 垂径定理的综合应用 例1. 一水平放置的圆柱型水管的横截面如图5－1所示，如果水管横截面的半径 是‎13cm，水面宽，则水管中水深是_______cm. 图5－1‎ 例2. 如图5－2，某地有一座圆弧形拱桥，桥下水面宽度为米，拱顶高出水面米，现有一艘宽米，船仓顶部为方形并高出水面米的货船要经过这里．问货船能否顺利通过这座拱桥？‎ ‎ 图5－2‎ 例3. 如图5－3，在某养殖场A处发现高致病性禽流感，为防止禽流感蔓延，政府规定离疫点‎3千米范围内为捕杀区；离疫点3至‎5千米范围内为免疫区.现有一条笔直的公路EB通疫区，若在捕杀区内CD＝‎4千米，问这条公路在改免疫区内多少千米？‎ E ‎ C ‎ D ‎ B ‎ ‎.A ‎ 图5－3‎ ‎【拓展提升】‎ 例1. 如图6－1，已知在⊙中，弦，且，垂足为，于， 于.（1）求证：是正方形.（2）若，，求圆心到弦和的距离.‎ A ‎ O ‎ D ‎ C ‎ B ‎ E ‎ F ‎ ‎ 图6－1 ‎ 例2. 如图6－2，AB是⊙O的直径,P是AB上一动点，C、D是⊙O的两点，有∠CPB=∠DPB.‎ ‎ 求证：PC=PD.‎ A ‎ B ‎ C ‎ D ‎ P ‎ O . ‎ ‎ 图6－2‎ 例3. 已知：如图6－3，A,B是半圆O上的两点，CD是⊙的直径，∠AOD＝800，B是 中点.‎ ‎ （1）在CD上求作一点P，使得AP+PB最短；C ‎ D ‎ O ‎ A ‎ B. ‎ （2）若CD=‎4cm，求AP+PB的最小值.‎ 图6－3‎ 例4. 如图6－4，AB是⊙O的直径，CD是弦，AE⊥CD于E ，BF⊥CD于F .求证： CE=DF ；OE=OF.‎ C ‎ O ‎ A ‎ B ‎ E ‎ F ‎ D ‎ ‎ 图6－4‎ 变式题1. 如图6－5，⊙的直径和弦相交于点，，，垂足分别是，．‎ ‎(1)求证：．‎ ‎(2)若，，求的值．‎ ‎ 图6－5‎ 变式题2：如果弦CD是动弦，与直径AB不相交，AE⊥CD于E ，BF⊥CD于F，此时是否有：‎ ‎ CE=DF ；OE=OF.如果有请证明，如果不成立，请说明.‎