人教版九年级数学上册同步测试题课件（10） 22页

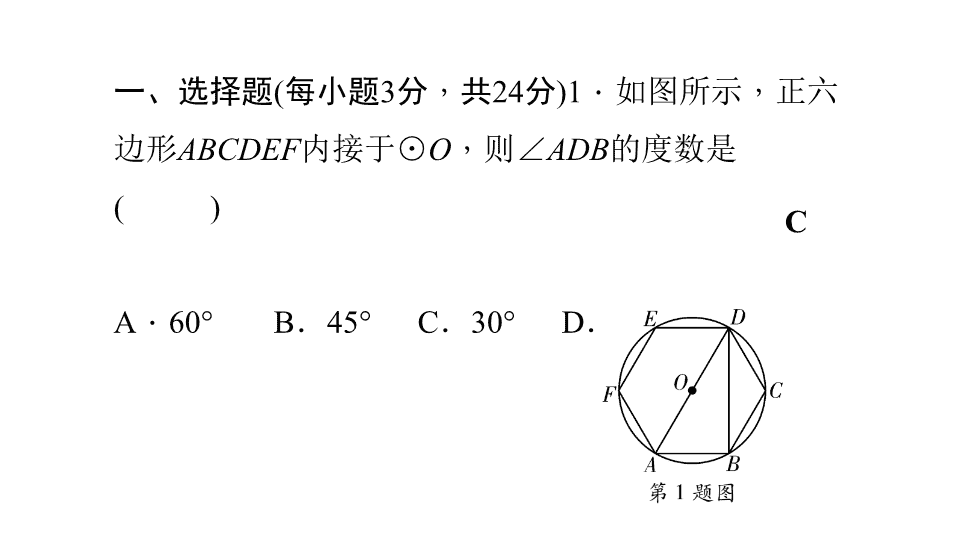
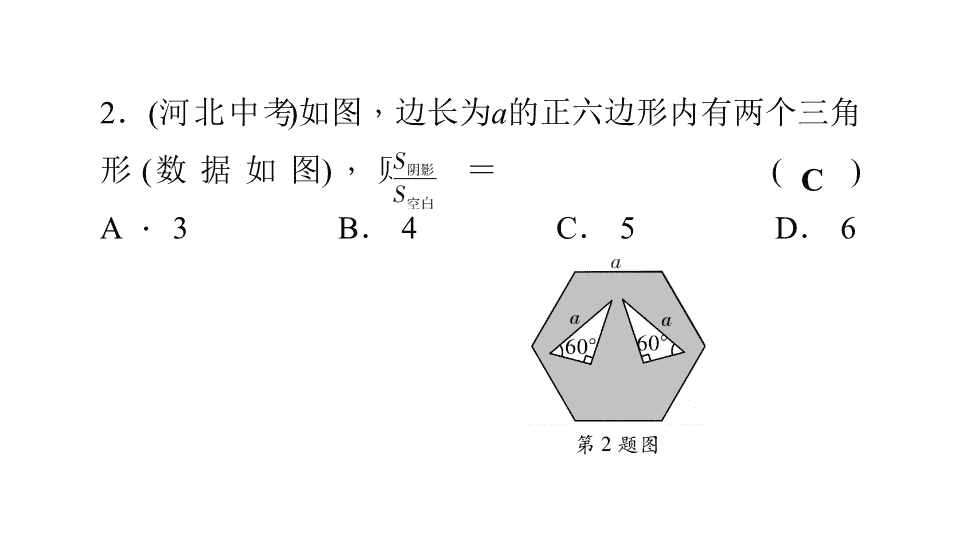
周周测 ( 十 )(24.3 － 24.4) 时间： 45 分钟　满分： 100 分　姓名： ________ C 一、选择题 ( 每小题 3 分 ， 共 24 分 ) 1 ． 如图所示 ， 正六边形 ABCDEF 内接于 ⊙ O ， 则 ∠ ADB 的度数是 ( 　 　 ) A ． 60 ° B ． 45 ° C ． 30° D ． 22.5° C 2 ． ( 河北中考 ) 如图 ， 边长为 a 的正六边形内有两个三角形 ( 数据如图 ) ， 则 ＝ ( ) A ． 3 B ． 4 C ． 5 D ． 6 B 3 ． 正六边形 ABCDEF 内接于 ⊙ O ， 正六边形的周长是 12 ， 则 ⊙ O 的半径是 ( 　 　 ) A. B ． 2 C ． 2 D .2 4 ． ( 遵义中考 ) 已知圆锥的底面积为 9 π cm 2 ， 母线长为 6 cm ， 则圆锥的侧面积是 ( ) A ． 18 π cm 2 B ． 27π cm 2 C ． 18 cm 2 D ． 27 cm 2 　 A 5 ． 如图 ， ⊙ O 的半径为 3 ， 四边形 ABCD 内接于 ⊙ O ， 连接 OB ， OD ， 若 ∠ BOD ＝ ∠ BCD ， 则 的长 ( ) A ． π B. π C ． 2π D ． 3π C 6 ． ( 山西中考 ) 如图是某商品的标志图案 ， AC 与 BD 是 ⊙ O 的两条直径 ， 首尾顺次连接点 A ， B ， C ， D ， 得到四边形 ABCD . 若 AC ＝ 10 cm ， ∠ BAC ＝ 36° ， 则图中阴影部分的面积为 ( 　 　 ) A ． 5 π cm 2 B ． 10π cm 2 C ． 15 π cm 2 D ． 20π cm 2 A 7 ． ★ 如图 ， 在 Rt △ ABC 中 ， ∠ ACB ＝ 90° ， AC ＝ BC ＝ 1 ， 将 Rt △ ABC 绕点 A 逆时针旋转 30° 后得到 Rt △ ADE ， 点 B 经过的路径为 ， 则图中阴影部分的面积是（ ）　 A. B. C. D. C 8 ． 如图 ， 在 △ ABC 中 ， CA ＝ CB ， ∠ ACB ＝ 90° ， 以 AB 的中点 D 为圆心 ， 作圆 心角为 90° 的扇形 DEF ， 点 C 恰在 上．设 ∠ BDF ＝ α (0° ＜ α ＜ 90°) ， 当 α 由小到大变化时 ， 图中阴影部分的面积 ( 　 　 ) A ． 由小变大 B ． 由大变小 C ． 不变 D ． 先由小变大 ， 后由大变小 二、填空题 ( 每小题 4 分 ， 共 24 分 ) 9 ． 半径为 R 的圆内接正三角形、正方形和正六边形的边长之比为 . 10 ． 半径为 9 cm 的圆中 ， 长为 12 π cm 的一条弧所对的圆心角的度数为 . 11 ． ( 聊城中考 ) 已知圆锥形工件的底面圆的直径是 40 cm ， 母线长 30 cm ， 其侧面展开图圆心角的度数为 . 12 ． ( 丽水中考 ) 如图 ， 在 △ ABC 中 ， AB ＝ AC ， 以 AB 为直径的 ⊙ O 分别与 BC ， AC 交于点 D ， E ， 过 D 作 ⊙ O 的切线 DF ， 交 AC 于点 F . 若 ⊙ O 的半径 为 4 ， ∠ CDF ＝ 22.5° ， 则阴影部分的面积为 . 13 ． ( 鄂州中考 ) 圆锥体的底面圆的周长为 6 π ， 侧面积为 12 π ， 则该圆锥体的高为 . 14 ． ( 上海中考 ) 我们规定：一个正 n 边形 ( n 为整数 ， n ≥ 4 ) 的最短对角线与最长对角线长度的比值叫做这个正 n 边形的 “ 特征值 ” ， 记为 λ n ， 那么 λ 6 ＝ . 三、解答题 ( 共 52 分 ) 15 ． (10 分 ) 如图所示 ， 正五边形 ABCDE 的对角线 AC 和 BE 相交于点 M . 求证： (1) AC ∥ DE ； (2) ME ＝ AE . 证明： (1) 由题意得 ∠ EDC ＝ × 3 × = 108° ， ∠ DCA ＝ × 2 × ＝ 72° ， ∴∠ EDC ＋ ∠ DCA ＝ 108° ＋ 72° ＝ 180° ， ∴ AC ∥ DE. (2) 由题意得 ∠ DEB ＝ ∠ EAC ＝ × 2 × ＝ 72°. ∵ AC ∥ DE ， ∴∠ AME ＝ ∠ DEB ＝ 72° ， ∴∠ AME ＝ ∠ EAC ， ∴ ME ＝ AE. 　 16 ． (10 分 ) 一个几何体由圆锥和圆柱组成 ， 其尺寸如图所示 ， 求该几何体的全面积 ( 即表面积 ) 是多少？ ( 结果保留 π ) 解：圆锥的母线长是： . 圆锥的侧面积是： × 8 π × 5 ＝ 20 π . 圆柱的侧面积是： 8 π × 4 ＝ 32 π. 几何体的下底面面积是： π × 4 2 ＝ 16 π . 所以该几何体的全面积 ( 即表面积 ) 为 20 π ＋ 32 π ＋ 16 π ＝ 68 π . 　 17 ． (10 分 ) 如图 ， 把 R t △ ABC 的斜边 AB 放在直线 l 上 ， 按顺时针方向在 l 上转动两次 ， 使它转到 △ A ″ B ″ C ′ 的位置上 ， 设 ∠ A ＝ 30° ， BC ＝ 1 ， 则顶点 A 运动到点 A ″ 的位置时 ， 点 A 经过的路线与直线 l 所围成的面积是多少？ 解：点 A 经过的路线与直 线 l 所围成的面积是由 S 扇形 ABA′ ， S △ A ′ BC ′ ， S 扇形 A′C′A″ 组成． ∵ ∠ C ＝ 90° ， BC ＝ 1 ， ∠ A ＝ 30 ° ， 可求得 AC ＝ ， AB ＝ 2 ， ∠ ABC ＝ 60° . S 扇形 ABA′ ＝ × 2 2 ＝ π ， S △ A ′ BC ′ ＝ × 1 × ＝ ， S 扇形 A′C′A″ ＝ × ( ) 2 ＝ π ， S ＝ π ＋ ＋ π ＝ π ＋ . 　 18 ． (10 分 ) 如图 ， 圆心角都是 90° 的扇形 OAB 与扇形 OCD 叠放在一起 ， 连接 AC ， BD . (1) 求证： AC ＝ BD ； (2) 若图中阴影部分的面积是 π cm 2 ， OA ＝ 2 cm ， 求 OC 的长． ( 1 ) 证明： ∵∠ AOB ＝ ∠ COD ＝ 90° ， ∴∠ AOC ＋ ∠ AOD ＝ ∠ BOD ＋ ∠ AOD ， ∴∠ AOC ＝ ∠ BOD. ∵ AO ＝ BO ， CO ＝ DO ， ∴△ AOC ≌△ BOD ( SAS ) ， ∴ AC ＝ BD. ( 2 ) 解：根据题意得 S 阴影 ＝ ∴ π ＝ ， 解得 OC ＝ 1 cm . 　 19 ． (12 分 ) 如图 ① 是某校存放学生自行车的车棚的示意图 ( 尺寸如图所示 ， 单位： m ) ， 车棚顶部是圆柱侧面的一部分 ， 其展开图是矩形 ， 如图 ② 是车棚顶部截面的示意图 ， 所在圆的圆心为点 O ， 车棚顶部是用一种帆布覆盖的 ， 求覆盖棚顶的帆布的面积． ( 不考虑接缝等因素 ， 计算结果保留 π ) 　　 解：连接 OB ， 过点 O 作 OE ⊥ AB ， 垂足为 E ， 交 于 F ， 由垂径定理 ， 知 E 是 AB 的中点 ， F 是 的中点 ， 从而 EF 是弓形的高． ∴ AE ＝ AB ＝ 2 m ， EF ＝ 2 m. 设半径为 R m ， 则 OE ＝ ( R － 2 ) m. 在 Rt △ AOE 中 ， 由勾 股定理 ， 得 R 2 ＝ ( R － 2 ) 2 ＋ ( 2 ) 2 ， 解得 R ＝ 4. ∴ OE ＝ 4 － 2 ＝ 2 ( m ) ．在 Rt △ AEO 中 ， AO ＝ 2OE ， ∴∠ OAE ＝ 30° ， ∠ AOE ＝ 60° ， ∴∠ AOB ＝ 120° ， ∴ 的长为 m. 故帆布的面积为 × 60 ＝ 160 π m 2 .