2019年全国中考真题分类汇编：统计与概率的实际应用（解答题） 98页

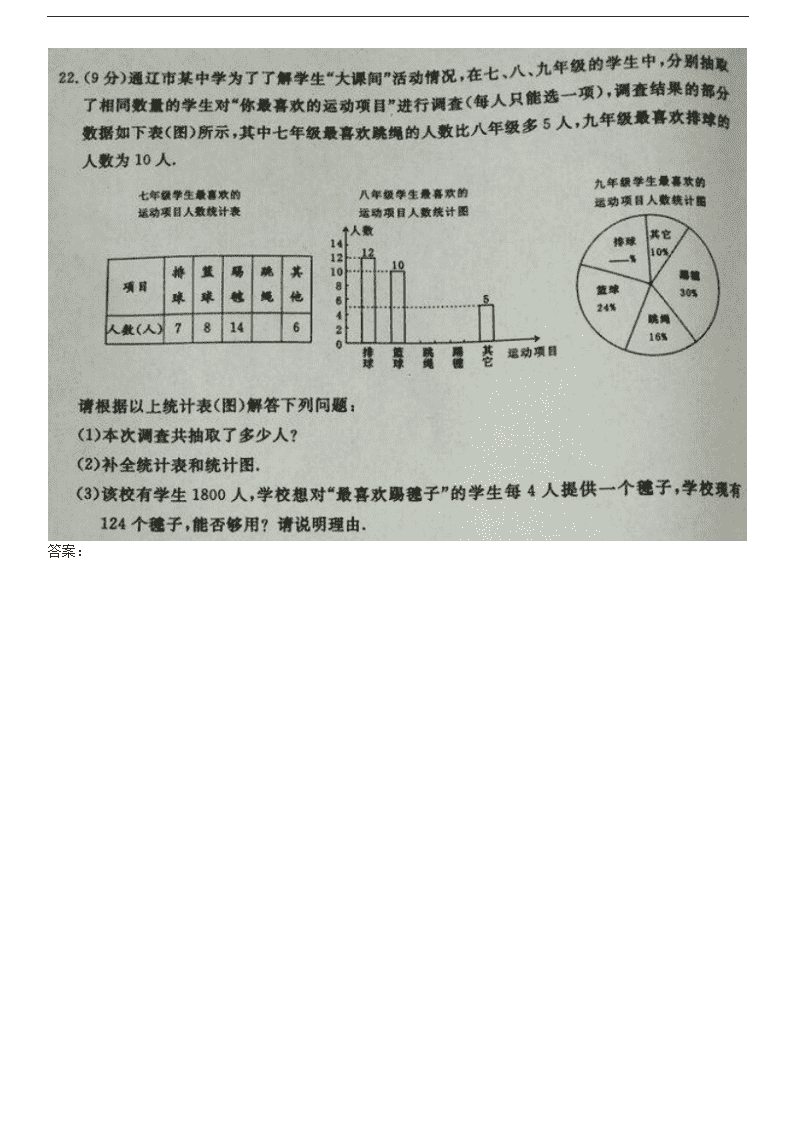
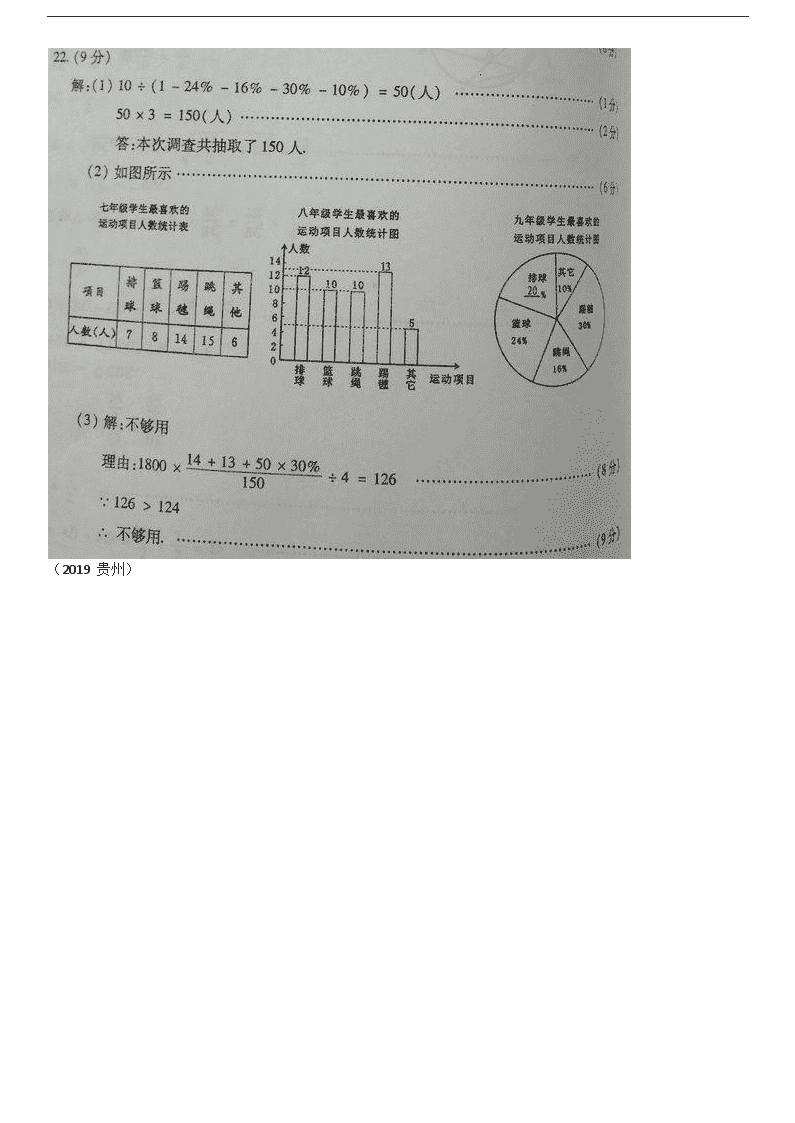
（分类）滚动小专题（十三） 统计与概率的实际应用（解答题） 类型 1 统计的实际应用 类型 2 概率的实际应用 类型 3 统计与概率的综合应用 类型 1 统计的实际应用 （2019 武汉） 19．（本题 8分）为弘扬中华传统文化，某校开展“双剧进课堂”的活动，该校童威随机抽取部分学生，按四个类别：A 表示“很喜欢”，B表示“喜欢”，C表示“一般”，D表示“不喜欢”，调查他们对汉剧的喜爱情况，将结果绘制成如下两 幅不完整的统计图，根据图中提供的信息，解决下列问题： (1) 这次共抽取_________名学生进行统计调查，扇形统计图中，D类所对应的扇形圆心角的大小为__________ (2) 将条形统计图补充完整 (3) 该校共有 1500名学生，估计该校表示“喜欢”的 B类的学生大约有多少人？ 各类学生人数条形统计图 各类学生人数扇形统计图 答案： （2019 通辽） 答案： （2019 贵州） （2019 云南） 17.(本小题满分 8分) 某公司销售部有書业员 15人，该公司为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对 营业员进行适当的奖励，为了确定一个适当的月销售目标，公司有关部门统计了这 15 人某月的销售量，如下表所 示： 月销售量/件数 1770 480 220 180 120 90 人数 1 1 3 3 3 4 （1）直接写出这 15名营业员该月销售量数据的平均数、中位数、众数； （2）如果想让一半左右的营业员都能达到月销售目标，你认为(1)中的平均数、中位数、众数中，哪个最适合 作为月销售目标?请说明理由． 温馨提示： （2019 吉林） （2019 大庆） （2019 桂林） （2019 玉林） （2019 齐齐哈尔） （2019 绥化） 答案： （2019 龙东地区） 答案： （2019 长沙） 21．（8分）某学校开展了主题为“垃圾分类，绿色生活新时尚”的宣传活动．为了解学生对垃圾分类知识的掌握情 况，该校环保社团成员在校园内随机抽取了部分学生进行问卷调查，将他们的得分按优秀、良好、合格、待合格 四个等级进行统计，并绘制了如下不完整的统计表和条形统计图． 等级 频数 频率 优秀 21 42% 良好 m 40% 合格 6 n% 待合格 3 6% （1）本次调查随机抽取了 50 名学生；表中 m＝ 20 ，n＝ 12 ； （2）补全条形统计图； （3）若全校有 2000名学生，请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人． 【分析】（1）用优秀的人数除以优秀的人数所占的百分比即可得到总人数； （2）根据题意补全条形统计图即可得到结果； （3）全校 2000名乘以“优秀”和“良好”等级的学生数所占的百分比即可得到结论． 【解答】解：（1）本次调查随机抽取了 21÷42%＝50名学生，m＝50×40%＝20，n＝ ×100＝12， 故答案为：50，20，12； （2）补全条形统计图如图所示； （3）2000× ＝1640人， 答：该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有 1640人． 【点评】本题考查的是条形统计图，读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清 楚地表示出每个项目的数据． （2019 北部湾） 答案： （2019 河南） （2019 贵港）答案： （2019 河池） （2019 湘西） 22.（本题 8分）“扫黑除恶”受到广大人民的关注，某中学对部分学生就“扫黑除恶”知识的了解程度， 采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图，请你 根据统计图中所提供的信息解答下列问题： （1）接受问卷调查的学生共有 人，扇形统计图中“很了解”部分所对应扇形的圆心角为 ； （2）请补全条形统计图； （3）若该中学共有学生 900人，请根据上述调查结果，估计该中学学生中对“扫黑除恶”知识达到“很 了解”和“基本了解”程度的总人数. （2019 常州） （2019 邵阳） （2019 益阳） 答案： （2019 北京） （2019 淮安） （2019 深圳） （2019 呼和浩特） 答案： （2019 宜昌） 20.（8分）某校在参加了宜昌市教育质量综合评价学业素养测试后，随机抽取八年级部分学生，针对发展水平四个 维度“阅读素养、数学素养、科学素养、人文素养”，开展了“你最需要提升的学业素养”问卷调查（每名学生必选且 只能选择一项）.小明、小颖和小雯在协助老师进行统计后，有这样一段对话： 小明：“选科学素养和人文素养的同学分别为 16人，12人.” 小颖：“选数学素养的同学比选阅读素养的同学少 4人” 小雯：“选科学素养的同学占样本总数的 20%” （1）这次抽样调查了多少名学生？ （2）样本总数中，选“阅读素养”、“数学素养”的学生各多少人？ （3）如图是调查结果整理后绘制成的扇形图.请直接在横线上补全相关百分比； （4）该校八年级有学生 400人，请根据调查结果估计全年级选择“阅读素养”的学生有多少人？ 答案 ： （2019 襄阳） （2019 咸阳 ） 20.（8分）某校为了解七、八年级学生一分钟跳绳情况，从这两个年级随机抽取50名学生进行测试，并对测试成绩 （一分钟跳绳次数）进行整理、描述和分析，下面给出了部分信息: 根据以上信息，回答下列问题： （1）表中a= ； （2）在这次测试中，七年级甲同学的成绩122次，八年级乙同学的成绩125次，他们的测试成绩，在各自年级所抽 取的50名同学中，排名更靠前的是 （填“甲”或“乙”），理由是 . （3）该校七年级共有500名学生，估计一分钟跳绳不低于116次的有多少人？ 答案： （2019 荆门） 答案： （2019 黔东南州） 23.(14 分)某地区在所有中学开展《老师,我想对你说》心灵信箱活动,为师生之间的沟通增设了一个书面交流的渠道. 为了解两年来活动开展的情况,某课题组从全地区随机抽取部分中学生进行问卷调查.对“两年来,你通过心灵信箱给 老师总共投递过封信?”这一调查项设有四个回答选项,选项 A:没有投过;选项 B:一封;选项 C:两; 选项 D:三封及以上. 根据接受问卷调查学生的回答,统计出各选项的人数以及所占百分比,分别绘制成如下条形统计图和扇形统计图: (1)此次抽样调查了 名学生，条形统计图中 m= ，n= ； (2)请将条形统计图补全; (3)接受问卷调查的学生在活动中投出的信件总数至少有 封； (4)全地区中学生共有 110 000 名,由此次调查估算,在此项活动中,全地区给老师投过信件的学生约有多少名？ （2019 天水） 20.（8 分）天水市某中学为了解学艺术社团活动的开展情况，在全校范围内随机抽取了部分学生，在“舞蹈、乐器、 声乐、戏曲、其它活动”项目中，围绕你最喜欢哪一项活动（每人只限一项）进行问卷调查，并将调查结果绘制成 如下两幅不完整的统计图. 请你根据统计图解答下列问题： （1）在这次调查中，一共抽查了 名学生； （2）请你不全条形统计图； （3）扇形统计图中喜欢“乐器”部分扇形的圆心角为 度; （4）请根据样本数据，估计该校 1200 名学生中喜欢“舞蹈”项目的共多少名学生. 答案： （2019 新疆） （2019 兰州） （2019 温州） 答案： （2019 贺州）答案： （2019 哈尔滨） 23、建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动， 为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学 生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且 只选一种)，学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图， 请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2) 请通过计算补全条形统计图；(3)如果海庆中学共有 1500 名学生,请你估计该校最想读 科技类书籍的学生有多少名 （2019 海南） （2019 乐山） 22.某校组织学生参加“安全知识竞赛”（满分为30分），测试结束后，张老师从七年级720名学生中随机地抽取部 分学生的成绩绘制了条形统计图，如图12所示．试根据统计图提供的信息，回答下列问题： 图12 （1）张老师抽取的这部分学生中，共有 ▲ 名男生， ▲ 名女生； （2）张老师抽取的这部分学生中，女生成绩．．．．的众数是 ▲ ； （3）若将不低于 27分的成绩定为优秀，请估计七年级720名学生中成绩为优秀的学生人数大约是多少. 答案：22.解：（1） 40 40 （2）27 （3） 396 80 44720 80 231227720    （人） （2019 苏州）答案： 23. (本题满分 8 分) 某校计划组织学生参加“书法”、“摄影”、“航模、“围棋”四个课外兴趣小组，要求每人必须参加，并且只能选择 其中一个小组，为了解学生对四个课外兴趣小组的选择情况，学校从全体学生中随机抽取部分学生进行问卷调查, 并把调查结果制成如图所示的扇形统计图和条形统计图(部分信息未给出)，请你根据给出的信息解答下列问题: (1)求参加这次问卷调查的学生人数，并补全条形统计图(画图后请标注相应的数据); (2) m=____,n=____; (3)若该校共有 1200 名学生，试估计该校选择“围棋”课外兴趣小组的学生有多少人？ （2019 成都） 答案： （2019 长沙） 答案： （2019 盐城） （2019 扬州） 21.（本题满分 8分）扬州市“五个一百工程”在各校普遍开展，为了了解某校学生每天课外阅读所 用的时间情况，从该校学生中随机抽取了部分学生进行问卷调查，并将结果绘制成如下不完整的频 数分布表和频数分布直方图. 根据以上信息，请回答下列问题： （1）表中 a= 120 ，b= 0.1 ； （2）请补全频数分布直方图； （3）若该校有学生 1200 人，试估计该校学生每天阅读时间超过 1小时的人数. 【解析】： （1）36÷0.3=120（人） 总共 120人，∴a=120 12÷120=0.1=b （2）如图 0.4×120=48（人） （3）1200×（0.4+0.1）=600 人 答：该校学生每天阅读时间超过 1 小时的人数为 600 人. 【考点】：数据的收集与整理，统计图的运用 （2019 杭州） 18.（本题 8 分） 称量五框水果的质量，若每框以 50kg 为基准，超过基准部分的千克数记为正数，不足基准部分的千克数记为负数， 甲组为实际称量读数，乙组为记录数据，并把所得数据整理成如下统计表和未完成的统计图（单位：kg）. （1）补充完整乙组数据的折线统计图； （2）①甲、乙两组数据的平均数分别为 甲x 、 乙x ，写出 甲x 和 乙x 之间的等量关系； ②甲、乙两组数据的方差分别为 2 甲S 、 2 乙S ，比较 2 甲S 和 2 乙S 的大小，并说明理由. 答案： （2019 江西） （2019 怀化） （2019 衡阳） （2019 重庆 B 卷） （2019 金华） 【答案】 （1）解：由统计表和扇形统计图可知： A 趣味数学的人数为 12 人，所占百分比为 20%， ∴总人数为：12÷20%=60（人）， ∴m=15÷60=25%， n=9÷60=15%， 答：m 为 25%，n为 15%. （2）由扇形统计图可得， D生活应用所占百分比为：30%， ∴D 生活应用的人数为：60×30%=18， 补全条形统计图如下， （3）解：由（1）知“数学史话”的百分比为 25%， ∴该校最喜欢“数学史话”的人数为：1200×25%=300（人）. 答：该校最喜欢“数学史话”的人数为 300 人. 【考点】用样本估计总体，扇形统计图，条形统计图 【解析】【分析】（1）根据统计表和扇形统计图中的数据，由总数=频数÷频率，频率=频数÷总数即可得答案.（2）由 扇形统计图中可得 D 生活应用所占百分比，再由频数=总数×频率即可求得答案.（3）由（1）知“数学史话”的百分比 为 25%，根据频数=总数×频率即可求得答案. （2019 枣庄） （2019 德州） 答案： （2019 泰安） （2019 达州） 【分析】（1）根据平均数的定义、中位数的定义、众数的定义进行解答即可； （2）①从极端值对平均数的影响作出判断即可； ②可用该店本周一到周日的日均营业额估计当月营业额． 【解答】解：（1）这组数据的平均数＝ ＝780（元）； 按照从小到大排列为 540、640、640、680、780、1070、1110， 中位数为 680元，众数为 640元； 故答案为：780，680，640； （2）①因为在周一至周日的营业额中周六、日的营业额明显高于其他五天的营业额， 所以去掉周六、日的营业额对平均数的影响较大， 故用该店本周星期一到星期五的日平均营业额估计当月的营业总额不合适； 故答案为：不合适； ②用该店本周一到周日的日均营业额估计当月营业额， 当月的营业额为 30×780＝23400（元）． （2019 衢州） 答案： （2019 重庆 A 卷） 21．每年夏季全国各地总有未成年人因溺水而丧失生命，令人痛心秩首．今年某校为确保学生安全，开展了“远离 溺水·珍爱生命”的防溺水安全知识竞赛．现从该校七、八年级中各随机抽取 10名学生的竞赛成绩（百分制） 进行整理、描述和分析（成绩得分用 x表示，共分成四组：A．80≤x≤85，B．85≤x≤90，C．90≤x≤95，D．95 ≤x≤100），下面给出了部分信息： 七年级 10名学生的竞赛成绩是：90，80，90，86，99，96，96，100，89，82 八年级 10名学生的竞赛成绩在 C组中的数据是:94，90，94 八年抽取的学生竞赛成绩扇形统计图 七、八年级抽取的学生竞赛成绩统计表 年级 七年级 八年级 平均数 92 92 中位数 93 b 21 题图 根据以上信息，解答下列问题： （1）直接写出上述图表中 a，b，c的值； （2）根据以上数据，你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好？请说明理由（一条理 由即可）； （3）该校七、八年级共 730人参加了此次竞赛活动，估计参加此次竞赛活动成绩优秀（x≧90）的学生人数是 多少？ 答案： 【分析】（1）根据中位数和众数的定义即可得到结论； （2）根据八年级的中位数和众数均高于七年级于是得到八年级学生掌握防溺水安全知识较好； （3）利用样本估计总体思想求解可得． （2019 天津） 纵数 c 100 方差 52 50．4 答案： （2019 淄博） （2019 聊城） 答案： （2019 青岛） 18．（本小题满分 6 分） 为了解学生每天的睡眠情况，某初中学校从全校 800 名学生中随机抽取了 40 名学生，调 查了他们平均每天的睡眠时间（单位： h） ，统计结果如下： 9，8，10.5，7，9，8，10，9.5，8，9，9.5，7.5，9.5，9，8.5，7.5，10，9.5，8，9， 7，9.5，8.5，9，7，9，9，7.5，8.5，8.5，9，8，7.5，9.5，10，9.5，8.5，9，8，9. 在对这些数据整理后，绘制了如下的统计图表： 睡眠时间分组统计表 睡眠时间分布情况 组别 睡眠时间分组 人数（频数） 1 7≤t＜8 m 2 8≤t＜9 11 3 9≤t＜10 n 4 10≤t＜11 4 请根据以上信息，解答下列问题： （1） m = ， n = ， a = ， b = ； （2）抽取的这 40 名学生平均每天睡眠时间的中位数落在 组（填组别） ； （3）如果按照学校要求，学生平均每天的睡眠时间应不少于 9 h，请估计该校学生中睡 眠时间符合要求的人数． 答案： （2019 临沂） 21.（7 分） 争创全国文明城市，从我做起，某学校在七年级开设了文明礼仪校本课程，为了解学生的学习情况，学校随机抽取 30 名学生进行测试，成绩如下（单位：分） 整理上面的数据得到频数分布表和频数分布直方图： 回答下列问题： （1）以上 30 个数据中，中位数是 ；频数分布表中a  ；b  ； （2）补全频数分布直方图； （3）若成绩不低于 86 分为优秀，估计该校七年级 300 名学生中，达到优秀等级的人数。 （2019 湖州） 答案： （2019 台州） （2019 绍兴） 答案： （2019 嘉兴） 21．在推进嘉兴市城乡生活垃圾分类的行动中，某社区为了了解居民掌握垃圾分类知识的 情况进行调查．其中 A、B 两小区分别有 500 名居民参加了测试，社区从中各随机 抽取 50 名居民成绩进行整理得到部分信息： 【信息一】A 小区 50 名居民成绩的频数直方图如下(每一组含前一个边界值， 不含后一个边界值)： 【信息二】上图中,从左往右 第四组的成绩如下 【信息三】A、B 两小区各 50 名居民成绩的平均数、中位数、众数、优秀率(80 分及以上为优秀)、方差等 数据如下(部分空缺)： 根据以上信息,回答下列问题： (1)求 A 小区 50 名居民成绩的中位数． (2)请估计 A 小区 500 名居民成绩能超过平均数的人数． (3)请尽量从多个角度，选择合适的统计量分析 A，B 两小区参加测试的居民掌握垃圾分类知识的情况． 答案： 答案： （2019 宁波） （2019 无锡）答案： 23．（本题满分 6分） 《国家学生体质健康标准》规定：体质测试成绩达到 90.0分及以上的为优秀；达到 80.0分至 89.9分的为良好； 达到 60.0分至 79.9分的为及格；59.9分及以下为不及格．某校为了了解九年级学生体质健康状况，从该校九年级 学生中随机抽取了 10%的学生进行体质测试，测试结果如下面的统计表和扇形统计图所示． 各等级学生人数分布扇形统计图 各等级学生平均分统计表 （1）扇形统 计图中“不及格”所占的百分比是 ； （2）计算所抽取的学生的测试成绩的平均分； （3）若所抽取的学生中所有不及格等级学生的总分恰好等于某一个良好等级学生的分数，请估计该九年级学生中 约有多少人达到优秀等级． 答案： 23． （1） 4% （2）92.1×52%+85.0×26%+69.2×18%+41.3×4%=84.1 （3）设总人数为 n个 , 80.0 ≤ 41.3×n×4%≤89.9 所以 48