江西专版2020中考数学复习方案第四单元图形的初步认识与三角形第17课时等腰三角形课件 29页

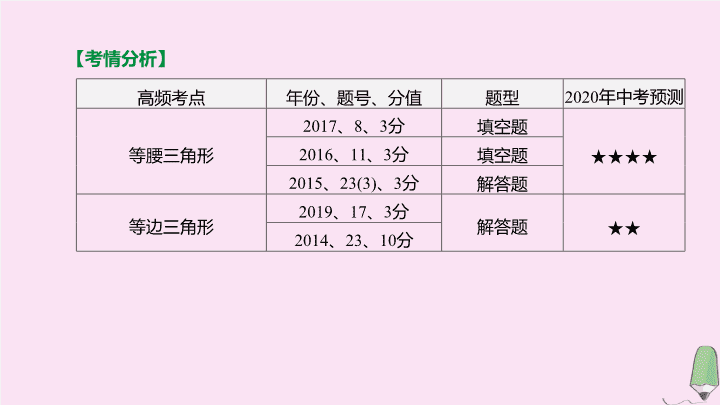
第 17 课时 等腰三角形 第四单元　图形的初步认识与三角形 【 考情分析 】 高频考点 年份、题号、分值 题型 2020 年中考预测 等腰三角形 2017 、 8 、 3 分 填空题 ★★★★ 2016 、 11 、 3 分 填空题 2015 、 23(3) 、 3 分 解答题 等边三角形 2019 、 17 、 3 分 解答题 ★★ 2014 、 23 、 10 分 定义 　 有 ① 　　　 相等的三角形叫做等腰三角形 . 相等的两边叫做腰 , 另一边叫做底边 , 两腰的夹角叫做顶角 , 腰和底边的夹角叫做底角   性质 (1) 两个底角相等 ( 简称 ② 　　 　　 );  (2) 顶角平分线、底边上的 ③ 　　　　 、底边上的高相互重合 ( 简称三线合一 );  (3) 是轴对称图形 , 有 ④ 　　　　 条对称轴   判定 (1) 在 △ ABC 中 , AB=AC ⇒△ ABC 是等腰三角形 ( 定义 ); (2) 在 △ ABC 中 , ∠ B= ∠ C ⇒△ ABC 是等腰三角形 面积 S = ah , 其中 a 是底边长 , h 是底边上的高 考点一　等腰三角形 考点聚焦 两边 等边对等角 中线 1 考点二　等边三角形 定义 三边都相等的三角形叫做等边三角形 性质 (1) 等边三角形的三个内角都相等 , 并且每一个角都等于 ⑤ 　　　　 ;  (2) 等边三角形三条角平分线的交点、三条高的交点、三条中线的交点重合 ; (3) 等边三角形是轴对称图形 , 有 ⑥ 　　　　 条对称轴   判定 (1) 三条边都相等的三角形是等边三角形 ( 定义 ); (2) 三个角都相等的三角形是等边三角形 ; (3) 有一个角等于 60° 的等腰三角形是等边三角形 面积 S = a 2 , a 是等边三角形的边长 60° 3 考点三　线段的垂直平分线 定义 经过线段中点并且垂直于这条线段的直线叫做这条线段的垂直平分线 性质 线段垂直平分线上的点与这条线段两个端点的距离 ⑦ 　　　   判断 与一条线段两个端点距离相等的点 , 在这条线段的 ⑧ 　　　　　　 上   相等 垂直平分线 1 . 如图 17-1, 在 △ ABC 中 , AC=BC , ∠ A= 40°, 观察图中尺规作图的痕迹 , 可知∠ BCG 的度数为 ( 　　 ) A . 40° B . 45° C . 50° D . 60° 题组一　必会题 对点演练 C 图 17-1 2 . 如图 17-2, AB ∥ CD , AD=CD , ∠ 1 = 50°, 则∠ 2 的度数是 ( 　　 ) A . 55° B . 60° C . 65° D . 70° 图 17-2 [ 答案 ] C 图 17-3 B 4 . [2019· 成都 ] 如图 17-4, 在 △ ABC 中 , AB=AC , 点 D , E 都在边 BC 上 , ∠ BAD= ∠ CAE , 若 BD= 9, 则 CE 的长为 　　　　 .  9 图 17-4 题组二　易错题 【 失分点 】 忽视等腰三角形的腰与底边的区别 , 底角与顶角的区别导致错误 ; 受片面思维的影响 , 忽视等腰三角形腰上的高的不同情况导致漏解 . 5 . [2019· 广安 ] 等腰三角形的两边长分别为 6 cm,13 cm, 其周长为 　　　 cm .  [ 答案 ] 32 　 [ 解析 ] 由题意知 , 应分两种情况 :(1) 当腰长为 6 cm 时 , 三角形三边长分别为 6,6,13, 又 6+6 < 13, 不能构成三角形 ; (2) 当腰长为 13 cm 时 , 三角形三边长分别为 6,13,13, 周长 = 2×13+6 = 32(cm) . 故答案为 32 . 6 . 等腰三角形一个外角等于 110°, 则其底角为 　　　　 .  [ 答案 ] 55° 或 70° 7 . 等腰三角形一腰上的高与另一腰的夹角是 50°, 则这个等腰三角形的底角为 　　　　 .  [ 答案 ] 70° 或 20° 考向一　等腰三角形的判定与性质 例 1 [2019· 衢州 ] “ 三等分角 ” 大约是在公元前五世纪由古希腊人提出来的 , 借助如图 17-5 所示的 “ 三等分角仪 ” 能三等分任一角 . 这个三等分角仪由两根有槽的棒 OA , OB 组成 , 两根棒在 O 点相连并可绕 O 转动、 C 点固定 , OC=CD=DE , 点 D , E 可在槽中滑动 . 若∠ BDE= 75°, 则∠ CDE 的度数是 ( 　　 ) A . 60° B . 65° C . 75° D . 80° 图 17-5 [ 答案 ] D 　 [ 解析 ] ∵ OC=CD=DE , ∴∠ O= ∠ ODC , ∠ DCE= ∠ DEC , ∴∠ DCE= ∠ O + ∠ ODC= 2 ∠ ODC. ∵∠ O + ∠ OED= 3 ∠ ODC= ∠ BDE= 75°, ∴∠ ODC= 25° . ∵∠ CDE + ∠ ODC= 180°- ∠ BDE= 105°, ∴∠ CDE= 105°- ∠ ODC= 80° . 故选 D . | 考向精练 | 1 . [2017· 江西 8 题 ] 如图 17-6 ①是一把园林剪刀 , 把它抽象为图② , 其中 OA=OB , 若剪刀张开的角为 30°, 则∠ A= 　　　　 度 .  图 17-6 [ 答案 ] 75 2 . [2019· 重庆 B 卷 ] 如图 17-7, 在 △ ABC 中 , AB=AC , AD ⊥ BC 于点 D. (1) 若∠ C= 42°, 求∠ BAD 的度数 ; (2) 若点 E 在边 AB 上 , EF ∥ AC 交 AD 的延长线于点 F. 求证 : AE=FE. 图 17-7 2 . [2019· 重庆 B 卷 ] 如图 17-7, 在 △ ABC 中 , AB=AC , AD ⊥ BC 于点 D. (2) 若点 E 在边 AB 上 , EF ∥ AC 交 AD 的延长线于点 F. 求证 : AE=FE. 图 17-7 考向二　与等腰三角形有关的多解问题 [ 答案 ] 15° 或 45° 或 75° 　 【 方法点析 】 解决与等腰三角形有关的问题时 , 一定要分清顶角和底角 , 底边和腰 , 高是在三角形内还是在三角形外 , 有些情况应该分类讨论 , 同时注意三角形的三边关系 . | 考向精练 | 1 . [2018· 义乌 ] 等腰三角形 ABC 中 , 顶角 A 为 40°, 点 P 在以 A 为圆心 , BC 长为半径的圆上 , 且 BP=BA , 则∠ PBC 的度数为 　　　　 .  [ 答案 ] 30° 或 110° 　 [ 解析 ] 根据题意作出图形 ( 如图 ), 当点 P 在直线 AB 的右侧时 , 连接 AP. ∵ AB=AC , ∠ BAC= 40°, ∴∠ ABC= ∠ C= 70° . ∵ AB=AB , AC=PB , BC=PA , ∴ △ ABC ≌△ BAP , ∴∠ ABP= ∠ BAC= 40°, ∠ PBC= ∠ ABC - ∠ ABP= 30° . 当点 P' 在 AB 的左侧时 , 同理可得∠ ABP'= 40°, ∴∠ P'BC= 40°+70° = 110° . 2 . [2019· 陇南 ] 定义 : 等腰三角形的顶角与其一个底角的度数的比值 k 称为这个等腰三角形的 “ 特征值 ” . 若等腰 △ ABC 中 , ∠ A= 80°, 则它的特征值 k= 　　　　 .  考向三　等边三角形的性质与判定 例 3 [2018· 嘉兴 ] 如图 17-8, 在 △ ABC 中 , AB=AC , D 为 AC 的中点 , DE ⊥ AB , DF ⊥ BC , 垂足分别为点 E , F , 且 DE=DF. 求证 :△ ABC 是等边三角形 . 图 17-8 证明 : ∵ AB=AC , ∴∠ B= ∠ C. ∵ DE ⊥ AB , DF ⊥ BC , ∴∠ DEA= ∠ DFC= 90° . ∵ D 为 AC 的中点 , ∴ DA=DC. 又∵ DE=DF , ∴ Rt△ ADE ≌ Rt△ CDF (HL) . ∴∠ A= ∠ C , ∴∠ A= ∠ B= ∠ C. ∴ △ ABC 是等边三角形 . | 考向精练 | 如图 17-9, 在等边三角形 ABC 中 , 点 D , E 分别在边 BC , AC 上 , 且 DE ∥ AB , 过点 E 作 EF ⊥ DE , 交 BC 的延长线于点 F. (1) 求∠ F 的度数 ; (2) 若 CD= 2, 求 DF 的长 . 图 17-9 解 :(1) ∵ △ ABC 为等边三角形 , ∴∠ B= 60° . ∵ DE ∥ AB , ∴∠ EDC= ∠ B= 60° . ∵ EF ⊥ DE , ∴∠ DEF= 90°, ∴∠ F= 90°- ∠ EDC= 30° . 如图 17-9, 在等边三角形 ABC 中 , 点 D , E 分别在边 BC , AC 上 , 且 DE ∥ AB , 过点 E 作 EF ⊥ DE , 交 BC 的延长线于点 F. (2) 若 CD= 2, 求 DF 的长 . 图 17-9 (2) 方法一 : ∵∠ ACB= 60°, ∠ EDC= 60°, ∴ △ EDC 为等边三角形 , ∴ DE=CD= 2 . ∵∠ DEF= 90°, ∠ F= 30°, ∴ DF= 2 DE= 4 . 方法二 : ∵ △ ABC 为等边三角形 , DE ∥ AB , ∴∠ EDF= ∠ B= ∠ A= ∠ DEC= 60°, ∴ CE=CD= 2 . ∵ EF ⊥ DE , ∴∠ DEF= 90°, ∴∠ CEF= 90°- ∠ DEC= 30° = ∠ F , ∴ CF=CE=CD= 2 . 故 DF=CD + CF= 4 .