2010年贵州省毕节地区中考数学试卷 16页

一、选择题（共15小题，每小题3分，满分45分）‎ ‎1、（2010•毕节地区）若|m﹣3|+（n+2）2=0，则m+2n的值为（　　）‎ ‎ A、﹣4 B、﹣1‎ ‎ C、0 D、4‎ 考点：非负数的性质：偶次方；非负数的性质：绝对值。‎ 分析：本题考查了非负数的性质：若两个非负数的和为0，则两个非负数都为0．‎ 解答：解：∵|m﹣3|+（n+2）2=0，‎ ‎∴m﹣3=0且n+2=0，‎ ‎∴m=3，n=﹣2．‎ 则m+2n=3+2×（﹣2）=﹣1．‎ 故选B．‎ 点评：初中阶段有三种类型的非负数：‎ ‎（1）绝对值；‎ ‎（2）偶次方；‎ ‎（3）二次根式（算术平方根）．‎ 当它们相加和为0时，必须满足其中的每一项都等于0．根据这个结论可以求解这类题目．‎ ‎2、（2010•毕节地区）2008北京奥运火炬传递的路程约为13.7万公里．近似数13.7万是精确到（　　）‎ ‎ A、十分位 B、十万位 ‎ C、万位 D、千位 考点：近似数和有效数字。‎ 专题：应用题。‎ 分析：近似数13.7万中的3，表示3万，是万位，因而13.7最后的数字7应是千位，则13.7万是精确到千位．‎ 解答：解：近似数13.7万是精确到千位．‎ 故选D．‎ 点评：13.7万就是一个用科学记数法表示的数字，确定这样的数精确到哪一位，可以先确定小数点前面的一位表示多少，是什么数位，最后看这个数的最后一位相应数位是什么，这个数就是精确到什么位．‎ ‎3、（2010•毕节地区）某县为发展教育事业，加强了对教育经费的投入，2007年投入3000万元，预计2009年投入5000万元．设教育经费的年平均增长率为x，根据题意，下面所列方程正确的是（　　）‎ ‎ A、3000（1+x）2=5000 B、3000x2=5000‎ ‎ C、3000（1+x%）2=5000 D、3000（1+x）+3000（1+x）2=5000‎ 考点：由实际问题抽象出一元二次方程。‎ 专题：增长率问题。‎ 分析：主要考查增长率问题，一般用增长后的量=增长前的量×（1+增长率），如果设教育经费的年平均增长率为x，根据“2007年投入3000万元，预计2009年投入5000万元”，可以分别用x表示2007以后两年的投入，然后根据已知条件可得出方程．‎ 解答：解：依题意得2009年投入为3000（1+x）2，‎ ‎∴3000（1+x）2=5000．‎ 故选A．‎ 点评：找到关键描述语，就能找到等量关系，是解决问题的关键．同时要注意增长率问题的一般规律．‎ ‎4、（2010•毕节地区）有一人患了流感，经过两轮传染后共有121人患了流感，每轮传染中平均一个人传染了（　　）个人．‎ ‎ A、12 B、11‎ ‎ C、10 D、9‎ 考点：一元二次方程的应用。‎ 专题：其他问题。‎ 分析：患流感的人把病毒传染给别人，自己仍然患病，包括在总数中．设每轮传染中平均一个人传染了x个人，则第一轮传染了x个人，第二轮作为传染源的是x+1人，则传染x（x+1）人，依题意列方程：1+x+x（1+x）=121，解方程即可求解．‎ 解答：解：设每轮传染中平均一个人传染了x个人，依题意得1+x+x（1+x）=121，即（1+x）2=121‎ 解方程得x1=10，x2=﹣12（舍去）‎ 故选C．‎ 点评：本题要注意的是，患流感的人把病毒传染给别人，自己仍然是患者，人数应该累加，这个问题和细胞分裂是不同的．‎ ‎5、（2010•毕节地区）已知方程x2+bx+a=0有一个根是﹣a（a≠0），则下列代数式的值恒为常数的是（　　）‎ ‎ A、ab B、‎ab ‎ C、a+b D、a﹣b 考点：一元二次方程的解。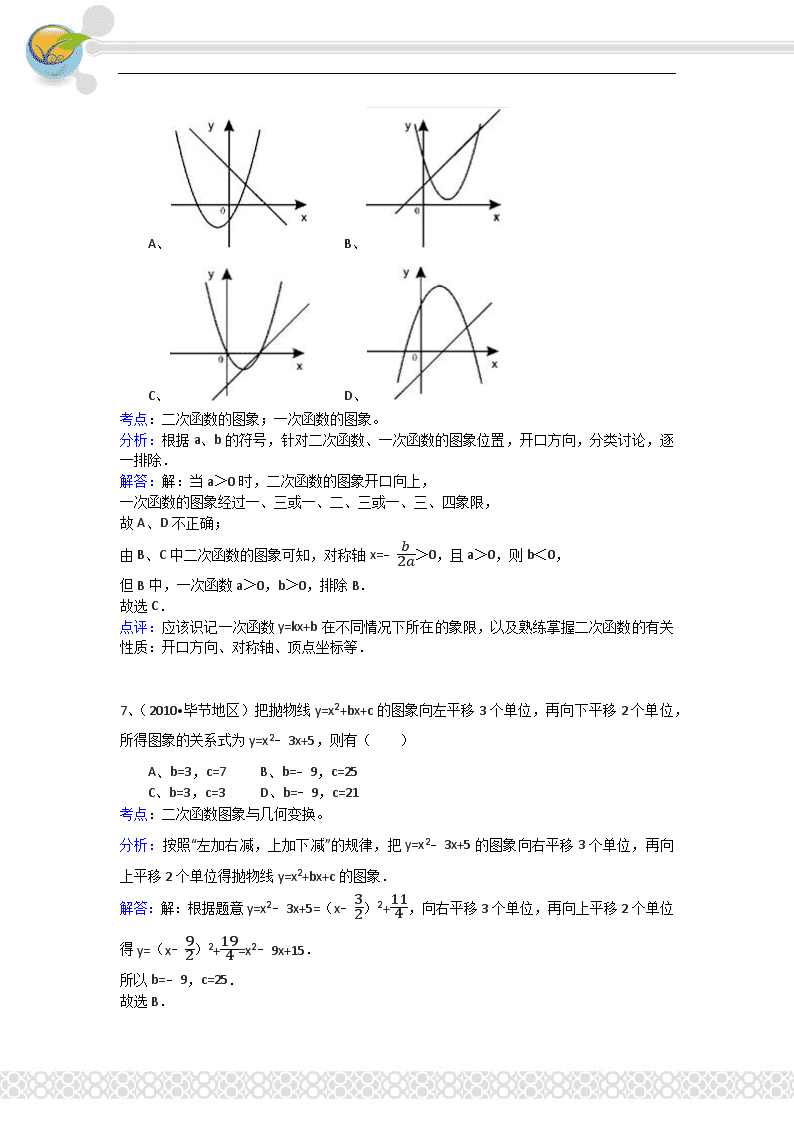‎ 分析：本题根据一元二次方程的根的定义，把x=﹣a代入方程，即可求解．‎ 解答：解：∵方程x2+bx+a=0有一个根是﹣a（a≠0）‎ ‎∴（﹣a）2+b（﹣a）+a=0，‎ 又∵a≠0，‎ ‎∴等式的两边同乘以a得a﹣b+1=0，故a﹣b=﹣1．‎ 故本题选D．‎ 点评：本题的考查的重点是方程根的定义，分析问题的方向比较明确，就是由已知入手推导、发现新的结论．‎ ‎6、（2010•毕节地区）函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是（　　）‎ ‎ A、 B、‎ ‎ C、 D、‎ 考点：二次函数的图象；一次函数的图象。‎ 分析：根据a、b的符号，针对二次函数、一次函数的图象位置，开口方向，分类讨论，逐一排除．‎ 解答：解：当a＞0时，二次函数的图象开口向上，‎ 一次函数的图象经过一、三或一、二、三或一、三、四象限，‎ 故A、D不正确；‎ 由B、C中二次函数的图象可知，对称轴x=﹣b‎2a＞0，且a＞0，则b＜0，‎ 但B中，一次函数a＞0，b＞0，排除B．‎ 故选C．‎ 点评：应该识记一次函数y=kx+b在不同情况下所在的象限，以及熟练掌握二次函数的有关性质：开口方向、对称轴、顶点坐标等．‎ ‎7、（2010•毕节地区）把抛物线y=x2+bx+c的图象向左平移3个单位，再向下平移2个单位，所得图象的关系式为y=x2﹣3x+5，则有（　　）‎ ‎ A、b=3，c=7 B、b=﹣9，c=25‎ ‎ C、b=3，c=3 D、b=﹣9，c=21‎ 考点：二次函数图象与几何变换。‎ 分析：按照“左加右减，上加下减”的规律，把y=x2﹣3x+5的图象向右平移3个单位，再向上平移2个单位得抛物线y=x2+bx+c的图象．‎ 解答：解：根据题意y=x2﹣3x+5=（x﹣‎3‎‎2‎）2+‎11‎‎4‎，向右平移3个单位，再向上平移2个单位得y=（x﹣‎9‎‎2‎）2+‎19‎‎4‎=x2﹣9x+15．‎ 所以b=﹣9，c=25．‎ 故选B．‎ 点评：此题不仅考查了对平移的理解，同时考查了学生将一般式转化顶点式的能力．‎ ‎8、（2010•毕节地区）函数y=‎1﹣kx的图象与直线y=x没有交点，那么k的取值范围是（　　）‎ ‎ A、k＞1 B、k＜1‎ ‎ C、k＞﹣1 D、k＜﹣1‎ 考点：反比例函数与一次函数的交点问题。‎ 专题：计算题。‎ 分析：根据正比例函数及反比例函数的性质作答．‎ 解答：解：直线y=x过一、三象限，要使两个函数没交点，‎ 那么函数y=‎1﹣kx的图象必须位于二、四象限，‎ 那么1﹣k＜0，则k＞1．‎ 故选A．‎ 点评：本题考查了反比例函数与一次函数的交点问题，结合函数图象解答较为简单．‎ ‎9、（2010•毕节地区）如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm2，则该半圆的半径为（　　）‎ ‎ A、‎（4+‎5‎）‎cm B、9cm ‎ C、‎4‎‎5‎cm D、‎6‎‎2‎cm 考点：正多边形和圆。‎ 分析：已知小正方形的面积即可求得边长，在直角△ACE中，利用勾股定理即可求解．‎ 解答：解：如图，圆心为A，设大正方形的边长为2x，圆的半径为R，‎ 则AE=BC=x，CE=2x；‎ ‎∵小正方形的面积为16cm2，‎ ‎∴小正方形的边长EF=DF=4，‎ 由勾股定理得，R2=AE2+CE2=AF2+DF2，即x2+4x2=（x+4）2+42，‎ 解得，x=4，‎ ‎∴R=‎4‎‎5‎cm．‎ 故选C．‎ 点评：本题利用了勾股定理，正方形的性质求解．‎ ‎10、（2010•毕节地区）已知圆锥的母线长是5cm，侧面积是15πcm2，则这个圆锥底面圆的半径是（　　）‎ ‎ A、1.5cm B、3cm ‎ C、4cm D、6cm 考点：圆锥的计算。‎ 分析：圆锥的侧面积=底面周长×母线长÷2，把相应的数值代入求解即可．‎ 解答：解：设底面半径为R，则底面周长=2πR，侧面积=‎1‎‎2‎×2πR×5=5πR=15π，‎ ‎∴R=3cm．‎ 故选B．‎ 点评：本题利用了圆的周长公式和扇形面积公式求解．‎ ‎11、（2010•湛江）观察下列几何体，主视图、左视图和俯视图都是矩形的是（　　）‎ ‎ A、 B、‎ ‎ C、 D、‎ 考点：简单几何体的三视图。‎ 分析：主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．‎ 解答：解：A、主视图为矩形，俯视图为圆，错误；‎ B、主视图为矩形，俯视图为矩形，正确；‎ C、主视图为等腰梯形，俯视图为圆环，错误；‎ D、主视图为三角形，俯视图为有对角线的矩形，错误．‎ 故选B．‎ 点评：本题重点考查了三视图的定义考查学生的空间想象能力．‎ ‎12、（2010•毕节地区）在正方形网格中，△ABC的位置如图，则cos∠B的值为（　　）‎ ‎ A、‎1‎‎2‎ B、‎‎2‎‎2‎ ‎ C、‎3‎‎2‎ D、‎‎3‎‎3‎ 考点：锐角三角函数的定义。‎ 专题：网格型。‎ 分析：找出∠B所在的直角三角形，根据三角函数的定义求解．‎ 解答：解：根据图形知∠B=45°，∴cos∠B=‎2‎‎2‎．‎ 故选B．‎ 点评：本题考查特殊角三角函数值的计算，特殊角三角函数值计算在中考中经常出现，题型以选择题、填空题为主．‎ ‎13、（2010•毕节地区）正方形ABCD在平面直角坐标系中的位置如图，将正方形ABCD绕D点顺时针方向旋转90°后，B点到达的位置坐标为（　　）‎ ‎ A、（﹣2，2） B、（4，1）‎ ‎ C、（3，1） D、（4，0）‎ 考点：坐标与图形变化-旋转。‎ 专题：网格型。‎ 分析：解题的关键是旋转的三要素：旋转中心，旋转方向，旋转角度，通过画图求解．‎ 解答：解：由图知B点的坐标为（2，4），根据旋转中心D，旋转方向顺时针，旋转角度90°，画图，从而得B点坐标为（4，0）．‎ 故选D．‎ 点评：本题涉及图形的旋转，体现了新课标的精神，抓住旋转的三要素：旋转中心，旋转方向，旋转角度，通过画图求解．‎ ‎14、（2010•毕节地区）如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图．那么关于该班40名同学一周参加体育锻炼时间的说法错误的是（　　）‎ ‎ A、极差是3 B、中位数为8‎ ‎ C、众数是8 D、锻炼时间超过8小时的有21人 考点：条形统计图；中位数；众数；极差。‎ 专题：图表型。‎ 分析：根据中位数、众数和极差的概念分别求得这组数据的中位数、众数和极差，由图可知锻炼时间超过8小时的有14+7=21人．即可判断四个选项的正确与否．‎ 解答：解：众数是一组数据中出现次数最多的数，即8；‎ 而将这组数据从小到大的顺序排列后，处于中间位置的那个数，由中位数的定义可知，这组数据的中位数不是8，是9；‎ 极差就是这组数中最大值与最小值的差10﹣7=3；‎ 锻炼时间超过8小时的有14+7=21人．‎ 所以，错误的是第二个．‎ 故选B．‎ 点评：考查了中位数、众数和极差的概念．本题为统计题，考查众数与中位数的意义，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会错误地将这组数据最中间的那个数当作中位数．‎ ‎15、（2010•毕节地区）在盒子里放有三张分别写有整式a+1，a+2，2的卡片，从中随机抽取两张卡片，把两张卡片上的整式分别作为分子和分母，则能组成分式的概率是（　　）‎ ‎ A、‎1‎‎3‎ B、‎‎2‎‎3‎ ‎ C、‎1‎‎6‎ D、‎‎3‎‎4‎ 考点：概率公式；分式的定义。‎ 专题：应用题。‎ 分析：列举出所有情况，看能组成分式的情况占所有情况的多少即为所求的概率．‎ 解答：解：分母含有字母的式子是分式，整式a+1，a+2，2中，抽到a+1，a+2做分母时组成的都是分式，共有3×2=6种情况，其中a+1，a+2为分母的情况有4种，所以能组成分式的概率=‎4‎‎6‎=‎2‎‎3‎．‎ 故选B．‎ 点评：用到的知识点为：概率等于所求情况数与总情况数之比．‎ 二、填空题（共5小题，每小题5分，满分25分）‎ ‎16、（2010•毕节地区）计算：a‎2‎a﹣3‎‎﹣‎‎9‎a﹣3‎= ．‎ 考点：分式的加减法。‎ 专题：计算题。‎ 分析：分式的加减运算中，同分母分式，那么分母不变，把分子直接相加减即可．‎ 解答：解：原式=‎（a﹣3）（a+3）‎a﹣3‎=a+3．‎ 点评：本题考查了分式的加减运算．最后要注意将结果化为最简分式．‎ ‎17、（2010•毕节地区）写出含有字母x，y的四次单项式 ．（答案不唯一，只要写出一个）‎ 考点：单项式。‎ 专题：开放型。‎ 分析：单项式的次数是指单项式中所有字母因数的指数和∴x3y，x2y2，xy3等都是四次单项式．‎ 解答：解：根据四次单项式的定义，x2y2，x3y，xy3等都符合题意（答案不唯一）．‎ 点评：考查了单项式的次数的概念．只要两个字母的指数的和等于4的单项式都符合要求．‎ ‎18、（2010•毕节地区）三角形的每条边的长都是方程x2﹣6x+8=0的根，则三角形的周长是 ．‎ 考点：解一元二次方程-因式分解法；三角形三边关系。‎ 分析：首先用因式分解法求得方程的根，再根据三角形的每条边的长都是方程x2﹣6x+8=0的根，进行分情况计算．‎ 解答：解：由方程x2﹣6x+8=0，得x=2或4．‎ 当三角形的三边是2，2，2时，则周长是6；‎ 当三角形的三边是4，4，4时，则周长是12；‎ 当三角形的三边长是2，2，4时，2+2=4，不符合三角形的三边关系，应舍去；‎ 当三角形的三边是4，4，2时，则三角形的周长是4+4+2=10．‎ 所以此三角形的周长是6或12或10．‎ 点评：本题一定要注意判断是否能够成三角形的三边．‎ ‎19、（2010•毕节地区）搭建如图①的单顶帐篷需要17根钢管，这样的帐篷按图②、图③的方式串起来搭建，则串7顶这样的帐篷需要 根钢管．‎ 考点：规律型：图形的变化类。‎ 专题：规律型。‎ 分析：根据题意分析可得：搭建如图①的单顶帐篷需要17根钢管，从串第2顶帐篷开始，每多串一顶帐篷需多用11根钢管．‎ 解答：解：第一顶帐篷用钢管数为17根；‎ 串二顶帐篷用钢管数为17+11×1=28根；‎ 串三顶帐篷用钢管数为17+11×2=39根；‎ 以此类推，串七顶帐篷用钢管数为17+11×6=83根．‎ 故应填83．‎ 点评：本题考查图形中的计数规律，要求学生的通过观察图形，分析、归纳并发现其中的规律，并应用规律解决问题．‎ ‎20、（2010•毕节地区）如图，AB为⊙O的弦，⊙O的半径为5，OC⊥AB于点D，交⊙O于点C，且CD=1，则弦AB的长是 ．‎ 考点：垂径定理；勾股定理。‎ 分析：连接AO，得到直角三角形，再求出OD的长，就可以利用勾股定理求解．‎ 解答：解：连接AO，‎ ‎∵半径是5，CD=1，‎ ‎∴OD=5﹣1=4，‎ 根据勾股定理，‎ AD=AO‎2‎‎﹣‎OD‎2‎=‎5‎‎2‎‎﹣‎4‎‎2‎；‎=3，‎ ‎∴AB=3×2=6，‎ 因此弦AB的长是6．‎ 点评：解答此题不仅要用到垂径定理，还要作出辅助线AO，这是解题的关键．‎ 三、解答题（共7小题，满分80分）‎ ‎21、（2010•毕节地区）解不等式组‎&1﹣2（x﹣1）≤5‎‎&‎3x﹣2‎‎2‎＜x+‎‎1‎‎2‎，并把解集在数轴上表示出来．‎ 考点：解一元一次不等式组；在数轴上表示不等式的解集。‎ 分析：先求出各不等式的解集，再求出其公共解集即可．‎ 解答：解：解不等式①，得x≥﹣1，（2分）‎ 解不等式②，得x＜3，（4分）‎ 不等式①、②的解集在数轴上表示如下：‎ ‎（6分）‎ ‎∴原不等式组的解集为﹣1≤x＜3．（8分）‎ 点评：求不等式的公共解，要遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．‎ ‎22、（2010•毕节地区）已知x﹣3y=0，求‎2x+yx‎2‎‎﹣2xy+‎y‎2‎•（x﹣y）的值．‎ 考点：分式的化简求值。‎ 专题：计算题。‎ 分析：首先将分式的分母分解因式，然后再约分、化简，最后将x、y的关系式代入化简后的式子中进行计算即可．‎ 解答：解：‎2x+yx‎2‎‎﹣2xy+‎y‎2‎‎•（x﹣y）‎=‎2x+y‎（x﹣y）‎‎2‎‎•（x﹣y）‎（2分）‎ ‎=‎2x+yx﹣y；（4分）‎ 当x﹣3y=0时，x=3y；（6分）‎ 原式=‎6y+y‎3y﹣y‎=‎7y‎2y=‎‎7‎‎2‎．（8分）‎ 点评：分式混合运算要注意先去括号；分子、分母能因式分解的先因式分解；除法要统一为乘法运算．‎ ‎23、（2010•毕节地区）如图，已知：平行四边形ABCD中，∠BCD的平分线CE交边AD于E，∠ABC的平分线BG交CE于F，交AD于G．求证：AE=DG．‎ 考点：平行四边形的性质；等腰三角形的判定与性质。‎ 专题：证明题。‎ 分析：由角的等量关系可分别得出△ABG和△DCE是等边三角形，得出AB=AG，DC=DE，则有AG=DE，从而证得AE=DG．‎ 解答：证明：∵四边形ABCD是平行四边形（已知），‎ ‎∴AD∥BC，AB=CD（平行四边形的对边平行，对边相等）‎ ‎∴∠GBC=∠BGA，∠BCE=∠CED（两直线平行，内错角相等）‎ 又∵BG平分∠ABC，CE平分∠BCD（已知），‎ ‎∴∠ABG=∠GBC，∠BCE=∠ECD（角平分线定义）‎ ‎∴∠ABG=∠GBA，∠ECD=∠CED．‎ ‎∴AB=AG，CE=DE（在同一个三角形中，等角对等边）‎ ‎∴AG=DE，‎ ‎∴AG﹣EG=DE﹣EG，即AE=DG．‎ 点评：本题考查平行四边形的性质、等腰三角形判定等知识．由等腰三角形的判定和等量代换推出AG=DE是关键．‎ 运用平行四边形的性质和等腰三角形的知识解答．‎ ‎24、（2010•毕节地区）如图，已知CD是△ABC中AB边上的高，以CD为直径的⊙O分别交CA，CB于点E，F，点G是AD的中点．求证：GE是⊙O的切线．‎ 考点：切线的判定；圆周角定理。‎ 专题：证明题。‎ 分析：要证GE是⊙O的切线，只要证明∠OEG=90°即可．‎ 解答：证明：（证法一）连接OE，DE，‎ ‎∵CD是⊙O的直径，‎ ‎∴∠AED=∠CED=90°，‎ ‎∵G是AD的中点，‎ ‎∴EG=‎1‎‎2‎AD=DG，‎ ‎∴∠1=∠2；‎ ‎∵OE=OD，‎ ‎∴∠3=∠4，‎ ‎∴∠1+∠3=∠2+∠4，‎ ‎∴∠OEG=∠ODG=90°，‎ 故GE是⊙O的切线；‎ ‎（证法二）连接OE，OG，‎ ‎∵AG=GD，CO=OD，‎ ‎∴OG∥AC，‎ ‎∴∠1=∠2，∠3=∠4．‎ ‎∵OC=OE，‎ ‎∴∠2=∠4，‎ ‎∴∠1=∠3．‎ 又OE=OD，OG=OG，‎ ‎∴△OEG≌△ODG，‎ ‎∴∠OEG=∠ODG=90°，‎ ‎∴GE是⊙O的切线．‎ 点评：本题考查切线的判定方法及圆周角定理运用．‎ ‎25、（2010•毕节地区）阅读对人成长的影响是很大的、希望中学共有1500名学生，为了了解学生课外阅读的情况，就“你最喜欢的图书类别”（只选一项）随机调查了部分学生，并将调查结果统计后绘制成如下统计表和条形统计图．请你根据统计图表提供的信息解答下列问题：‎ ‎（1）这次随机调查了 名学生；‎ ‎（2）把统计表和条形统计图补充完整；‎ ‎（3）随机调查一名学生，恰好是最喜欢文学类图书的概率是多少？‎ 考点：条形统计图；频数（率）分布表；概率公式。‎ 专题：阅读型。‎ 分析：（1）根据统计表中，科普的人数是45人，占0.15；根据频数与频率的关系，可知共有45÷0.15=300（人）；‎ ‎（2）根据统计表中的数据：易知其他数值；据此可补全条形图；‎ ‎（3）由条形图可知：喜欢文学类图书有96人，占总人数的32%；故随机调查一名学生，估计恰好是最喜欢文学类图书的概率是32%．‎ 解答：解：（1）这次随机调查的人数：45÷0.15=300（人）；（3分）‎ ‎（2）根据统计表中的数据：艺术的有78人，占26%，即频率为26%；文学的有300﹣78﹣45﹣81=96人，其频率0.26（6分）‎ 据此可补全条形图：‎ ‎（8分）‎ ‎（3）故随机调查一名学生，估计恰好是最喜欢文学类图书的概率是96÷300=32%．（9分）‎ 点评：本题考查的是条形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．用到的知识点为：总体数目=部分数目÷相应百分比．概率=所求情况数与总情况数之比．‎ ‎26、（2010•毕节地区）已知关于x的一元二次方程x2+（2m﹣1）x+m2=0有两个实数根x1和x2．‎ ‎（1）求实数m的取值范围；‎ ‎（2）当x12﹣x22=0时，求m的值．‎ 考点：根的判别式；根与系数的关系。‎ 专题：分类讨论。‎ 分析：（1）若一元二次方程有两实数根，则根的判别式△=b2﹣4ac≥0，建立关于m的不等式，求出m的取值范围；‎ ‎（2）由x12﹣x22=0得x1+x2=0或x1﹣x2=0；当x1+x2=0时，运用两根关系可以得到﹣2m﹣1=0或方程有两个相等的实根，据此即可求得m的值．‎ 解答：解：（1）由题意有△=（2m﹣1）2﹣4m2≥0，‎ 解得m≤‎‎1‎‎4‎，‎ 即实数m的取值范围是m≤‎‎1‎‎4‎；‎ ‎（2）由x12﹣x22=0得（x1+x2）（x1﹣x2）=0，‎ 若x1+x2=0，即﹣（2m﹣1）=0，解得m=‎‎1‎‎2‎，‎ ‎∵‎1‎‎2‎＞‎1‎‎4‎，‎ ‎∴m=‎‎1‎‎2‎不合题意，舍去，‎ 若x1﹣x2=0，即x1=x2∴△=0，由（1）知m=‎‎1‎‎4‎，‎ 故当x12﹣x22=0时，m=‎‎1‎‎4‎．‎ 点评：本题考查了一元二次方程根的判别式及根与系数关系，利用两根关系得出的结果必须满足△≥0的条件．‎ ‎27、（2010•毕节地区）某物流公司的快递车和货车每天往返于A、B两地，快递车比货车多往返一趟．图表示快递车距离A地的路程y（单位：千米）与所用时间x（单位：时）的函数图象．已知货车比快递车早1小时出发，到达B地后用2小时装卸货物，然后按原路、原速返回，结果比快递车最后一次返回A地晚1小时．‎ ‎（1）请在图中画出货车距离A地的路程y（千米）与所用时间x（时）的函数图象；‎ ‎（2）求两车在途中相遇的次数（直接写出答案）；‎ ‎（3）求两车最后一次相遇时，距离A地的路程和货车从A地出发了几小时？‎ 考点：一次函数的应用；分段函数。‎ 专题：压轴题。‎ 分析：（1）货车从出发到返回共10小时，所以前4小时一段、后4小时一段、中间2小时路程不变；‎ ‎（2）分别求出函数解析式解方程组即可．‎ 解答：解：（1）根据题意，图象经过（﹣1，0）、（3，200）和（5，200）、（9，0）．‎ 如图：‎ ‎（2）4次；‎ ‎（3）如图2，设直线EF的解析式为y=k1x+b1‎ ‎∵图象过（9，0），（5，200）‎ ‎∴‎‎&200=5k‎1‎+‎b‎1‎‎&0=9k‎1‎+‎b‎1‎ ‎∴‎‎&k‎1‎=﹣50‎‎&b‎1‎=450‎ ‎∴y=﹣50x+450 ①‎ 设直线CD的解析式为y=k2x+b2∵图象过（8，0），（6，200）‎ ‎∴‎‎&200=6k‎2‎+‎b‎2‎‎&0=8k‎2‎+‎b‎2‎ ‎∴‎‎&k‎2‎=﹣100‎‎&b‎2‎=800‎ ‎∴y=﹣100x+800 ②‎ 解由①②组成的方程组得：‎‎&x=7‎‎&y=100‎ ‎∴最后一次相遇时距离A地的路程为100km，货应从A地出发8小时．‎ 点评：本题主要考查二元一次方程组与一次函数的联系．‎ 参与本试卷答题和审题的老师有：‎ kuaile；zhjh；如来佛；lzhzkkxx；Linaliu；CJX；ln_86；huangling；MMCH；lanyuemeng；zhangCF；lanchong；zhehe；shenzigang；137-hui；wdxwzk；zxw；mama258；HJJ；littlenine；cook2360；路斐斐；hbxglhl；feng；mmll852；开心。（排名不分先后）‎ ‎2011年2月17日