重庆市第十一中学2018～2019学年度上期九年级数学视图与投影单元测试（北师大）含答案 6页

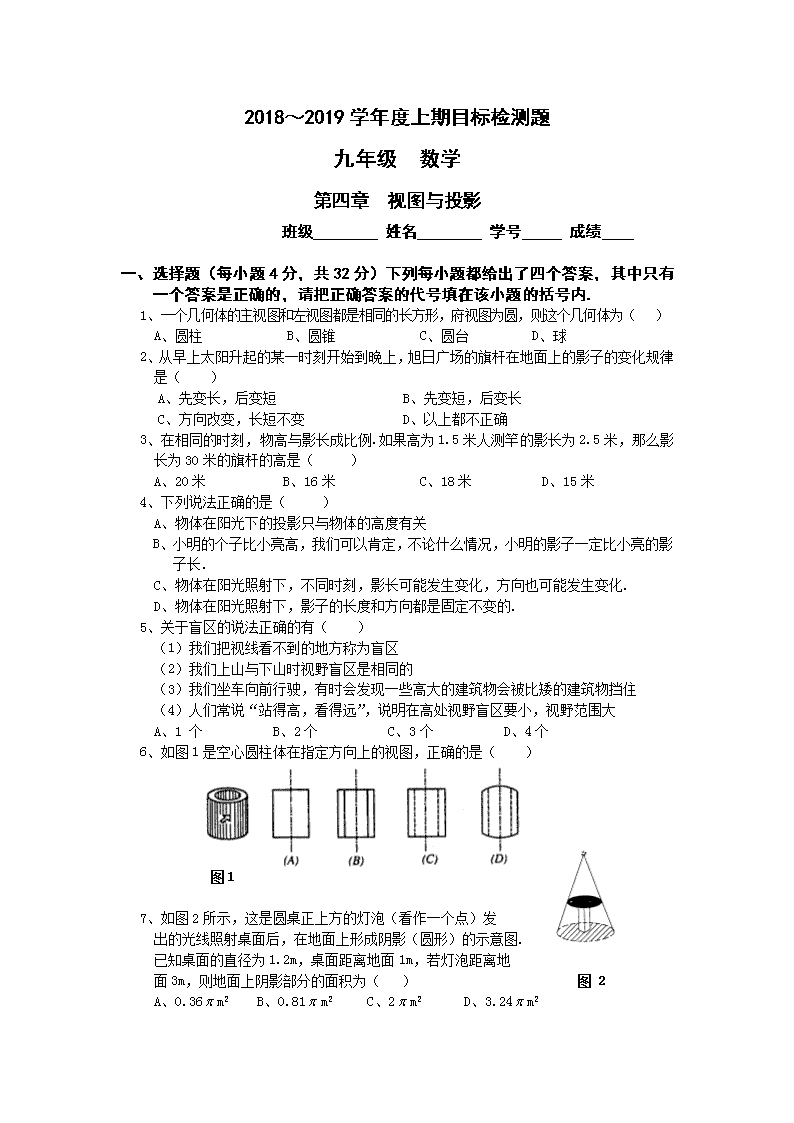
‎2018～2019学年度上期目标检测题 九年级 数学 ‎ 第四章 视图与投影 班级 姓名 学号 成绩 ‎ 一、选择题（每小题4分，共32分）下列每小题都给出了四个答案，其中只有一个答案是正确的，请把正确答案的代号填在该小题的括号内.‎ ‎1、一个几何体的主视图和左视图都是相同的长方形，府视图为圆，则这个几何体为（ ）‎ A、圆柱 B、圆锥 C、圆台 D、球 ‎2、从早上太阳升起的某一时刻开始到晚上，旭日广场的旗杆在地面上的影子的变化规律是（ ）‎ A、先变长，后变短 B、先变短，后变长 ‎ C、方向改变，长短不变 D、以上都不正确 ‎3、在相同的时刻，物高与影长成比例.如果高为1.5米人测竿的影长为2.5米，那么影长为30米的旗杆的高是（ ）‎ A、20米 B、16米 C、18米 D、15米 ‎4、下列说法正确的是（ ）‎ A、物体在阳光下的投影只与物体的高度有关 B、小明的个子比小亮高，我们可以肯定，不论什么情况，小明的影子一定比小亮的影子长.‎ C、物体在阳光照射下，不同时刻，影长可能发生变化，方向也可能发生变化.‎ D、物体在阳光照射下，影子的长度和方向都是固定不变的.‎ ‎5、关于盲区的说法正确的有（ ）‎ ‎（1）我们把视线看不到的地方称为盲区 ‎（2）我们上山与下山时视野盲区是相同的 ‎（3）我们坐车向前行驶，有时会发现一些高大的建筑物会被比矮的建筑物挡住 ‎（4）人们常说“站得高，看得远”，说明在高处视野盲区要小，视野范围大 A、1 个 B、2个 C、3个 D、4个 ‎6、如图1是空心圆柱体在指定方向上的视图，正确的是（ ）‎ ‎ ‎ 图1‎ ‎7、如图2所示，这是圆桌正上方的灯泡（看作一个点）发 出的光线照射桌面后，在地面上形成阴影（圆形）的示意图.‎ 已知桌面的直径为1.2m，桌面距离地面1m，若灯泡距离地 面3m，则地面上阴影部分的面积为（ ） 图 2‎ A、0.36m2 B、0.81m2 C、2m2 D、3.24m2‎ ‎8、如图（三）是小明一天上学、放学时看到的一根电线杆的影子的府视图，按时间先后顺序进行排列正确的是（ ）‎ ‎ （三）‎ A、（1）（2）（3）（4） B、（4）（3）（1）（2）‎ C、（4）（3）（2）（1） D、（2）（3）（4）（1）‎ 二、填空题（每小题3分，共21分）‎ ‎1、主视图、左视图、府视图都相同的几何体为 （写出两个）.‎ ‎2、太阳光线形成的投影称为 ，手电筒、路灯、台灯的光线形成的投影称为 .‎ ‎3、我们把大型会场、体育看台、电影院建为阶梯形状，是为了 .‎ ‎4、为了测量一根电线杆的高度，取一根2米长的竹竿竖直放在阳光下，2米长的竹竿的影长为1米，并且在同一时刻测得电线杆的影长为7.3米，则电线杆的高为 米.‎ ‎5、如果一个几何体的主视图、左视图都是等腰三角形，俯视图为圆，那么我们可以确定这个几何体是 .‎ ‎6、将一个三角板放在太阳光下，它所形成的投影是 ，也可能是 .‎ ‎7、身高相同的小明和小华站在灯光下的不同位置，如果小明离灯较远，那么小明的投影比小华的投影 .‎ 三、解答题（本题7个小题，共47分）‎ ‎1、某糖果厂为儿童设计一种新型的装糖果的不倒翁（如图4所示）‎ 请你为包装厂设计出它的主视图、左视图和府视图.‎ ‎ 图 4‎ ‎2、画出图5中三棱柱的主视图、左视图、俯视图.‎ ‎ 图 5‎ ‎3、画出图6中空心圆柱的主视图、左视图、俯视图.‎ ‎ 图 6‎ ‎4、如图7所示，屋顶上有一只小猫，院子里有一只小老鼠，若小猫看见了小老鼠，则小老鼠就会有危险，试画出小老鼠在墙的左端的安全区.‎ ‎ 图 7‎ ‎5、如图8为住宅区内的两幢楼，它们的高AB=CD=30m，两楼间的距离AC=30m，现需了解甲楼对乙楼的采光的影响情况，（1）当太阳光与水平线的夹角为30°角时，求甲楼的影子在乙楼上有多高（精确到0.1m，1.73）；（2）若要甲楼的影子刚好不落在乙楼的墙上，此时太阳与水平线的夹角为多少度？‎ ‎ 图 8‎ ‎6、阳光通过窗口照到教室内，竖直窗框在地面上留下2.1m长的影子[如图（9）所示]，已知窗框的影子DE到窗下墙脚的距离CE=3.9m，窗口底边离地面的距离BC=1.2m，试求窗口的高度（即AB的值）‎ ‎ 图 9‎ ‎7、一位同学想利用有关知识测旗杆的高度，他在某一时刻测得高为0.5m的小木棒的影长为0.3m，但当他马上测量旗杆的影长时，因旗杆靠近一幢建筑物，影子不全落在地面上，有一部分影子在墙上，他先测得留在墙上的影子CD=1.0m，又测地面部分的影长BC=3.0m，你能根据上述数据帮他测出旗杆的高度吗？‎ ‎ 图 10‎ 参考答案 一、选择题 1、A 2、B 3、C 4、C 5、C 6、C 7、B 8、B 二、填空题 1、正方体或圆；2、平行投影，中心投影；3、减小盲区；4、14.6；5、圆锥；6、三角形，一条线段；7、长。‎ 三、解答题 ‎1、 2、‎ ‎3、 4、略 ‎5、（1）如图，延长OB交DC于E，作EF⊥AB，交AB于F，‎ 在Rt△BEF中，∵EF=AC=30m，∠FEB=30°，∴BE=2BF.‎ 设BF=x,则 BE=2x.‎ 根据勾股定理知 BE2=BF2＋EF2 ∴（2x）2=x2+302 ‎ ‎∴(负值舍去)，∴（m）‎ 因此，EC=30－17.3=12.7（m）。‎ ‎（2）当甲幢楼的影子刚好落在点C处时，△ABC为等腰三角形，因此，当太阳光与水平线夹角为45°时，甲楼的影子刚好不落在乙楼的墙上。‎ ‎6、解：由于阳光是平行光线，即AE∥BD，‎ 所以∠AEC=∠BDC. 又因为∠C是公共角，‎ 所以△AEC∽△BDC，从而有.‎ 又AC=AB+BC，DC=EC－ED，EC=3.9，ED=2.1，BC=1.2，‎ 于是有，解得 AB=1.4(m)。‎ 答：窗口的高度为1.4m。‎ ‎7、能。旗杆的高度为6.0m。‎