2020年山东省济南市槐荫区中考数学一模试卷 14页

‎2020年山东省济南市槐荫区中考数学一模试卷 一、选择题（本大题共12个小题，每小题4分，共48分.在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎ ‎ ‎1. ‎9‎的算术平方根是（ ） ‎ A.‎−3‎ B.‎3‎ C.‎±3‎ D.‎‎81‎ ‎ ‎ ‎2. 如图所示的几何体，它的左视图是（ ） ‎ A. B. C. D.‎ ‎ ‎ ‎3. 新冠疫情牵动着每一个中国人的心，截至‎2020‎年‎3‎月‎11‎日上午‎9‎时，我国已累计治愈了‎62567‎名新冠肺炎患者，将数‎62567‎用科学记数法表示为（ ） ‎ A.‎62.567×‎‎10‎‎3‎ B.‎6.2567×‎‎10‎‎3‎ C.‎6.2567×‎‎10‎‎4‎ D.‎‎0.62567×‎‎10‎‎5‎ ‎ ‎ ‎4. 如图，AB // CD，‎∠B＝‎85‎‎∘‎，‎∠E＝‎27‎‎∘‎，则‎∠D的度数为（ ） ‎ A.‎45‎‎∘‎ B.‎48‎‎∘‎ C.‎50‎‎∘‎ D.‎‎58‎‎∘‎ ‎ ‎ ‎5. 下列计算错误的是（ ） ‎ A.‎(a‎3‎b)⋅(ab‎2‎)‎＝a‎4‎b‎3‎ B.xy‎2‎−‎1‎‎5‎xy‎2‎=‎4‎‎5‎xy‎2‎ C.a‎5‎‎÷‎a‎2‎＝a‎3‎ D.‎(−mn‎3‎‎)‎‎2‎＝m‎2‎n‎5‎ ‎ ‎ ‎ ‎6. 民族图案是数学文化中的一块瑰宝．下列图案中，是轴对称图形但不是中心对称图形的是‎(‎        ‎)‎ ‎ A. B. C. D. ‎ ‎ ‎ ‎7. 计算a‎2‎a−1‎‎−a−1‎的正确结果是（ ） ‎ A.‎−‎‎1‎a−1‎ B.‎1‎a−1‎ C.‎−‎‎2a−1‎a−1‎ D.‎‎2a−1‎a−1‎ ‎ ‎ ‎8. 小莹同学‎10‎个周综合素质评价成绩统计如下： ‎ 成绩（分）‎ ‎94‎ ‎95‎ ‎97‎ ‎98‎ ‎99‎ ‎100‎ 周数（个）‎ ‎1‎ ‎2‎ ‎2‎ ‎3‎ ‎1‎ ‎1‎ 这‎10‎个周的综合素质评价成绩的中位数和众数分别是（ ）‎ A.‎97.5 97‎ B.‎97 97‎ C.‎97.5 98‎ D.‎‎97 98‎ ‎ ‎ ‎9. 函数y=‎ax和一次函数y＝‎−ax+1(a≠0)‎在同一平面直角坐标系中的图象可能是（ ） ‎ A. B. C. D. ‎ 第25页 共28页 ◎ 第26页 共28页 ‎ ‎ ‎10. 如图，‎⊙O中，AB＝AC，‎∠ACB＝‎75‎‎∘‎，BC＝‎1‎，则阴影部分的面积是（ ） ‎ A.‎1+‎1‎‎6‎π B.‎1‎‎2‎‎+‎1‎‎6‎π C.‎1‎‎2‎‎+‎1‎‎3‎π D.‎‎1+‎1‎‎3‎π ‎ ‎ ‎11. 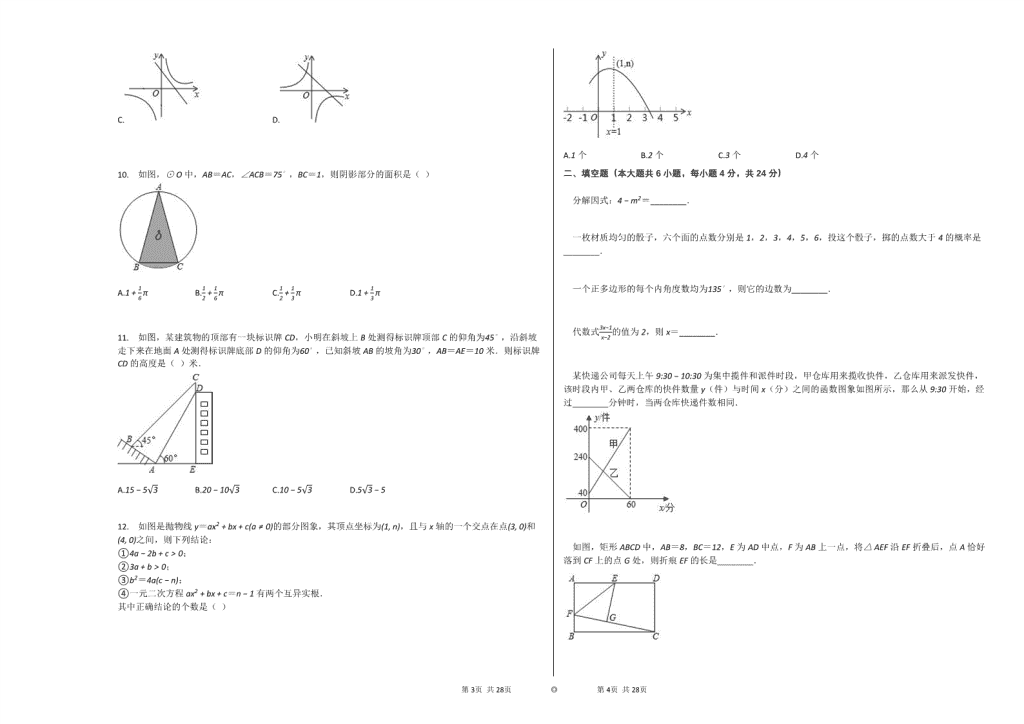如图，某建筑物的顶部有一块标识牌CD，小明在斜坡上B处测得标识牌顶部C的仰角为‎45‎‎∘‎，沿斜坡走下来在地面A处测得标识牌底部D的仰角为‎60‎‎∘‎，已知斜坡AB的坡角为‎30‎‎∘‎，AB＝AE＝‎10‎米．则标识牌CD的高度是（ ）米． ‎ A.‎15−5‎‎3‎ B.‎20−10‎‎3‎ C.‎10−5‎‎3‎ D.‎‎5‎3‎−5‎ ‎ ‎ ‎12. 如图是抛物线y＝ax‎2‎+bx+c(a≠0)‎的部分图象，其顶点坐标为‎(1, n)‎，且与x轴的一个交点在点‎(3, 0)‎和‎(4, 0)‎之间，则下列结论： ①‎4a−2b+c>0‎； ②‎3a+b>0‎； ③b‎2‎＝‎4a(c−n)‎； ④一元二次方程ax‎2‎+bx+c＝n−1‎有两个互异实根． 其中正确结论的个数是（ ） ‎ A.‎1‎个 B.‎2‎个 C.‎3‎个 D.‎4‎个 二、填空题（本大题共6小题，每小题4分，共24分）‎ ‎ ‎ ‎ 分解因式：‎4−‎m‎2‎＝________． ‎ ‎ ‎ ‎ 一枚材质均匀的骰子，六个面的点数分别是‎1‎，‎2‎，‎3‎，‎4‎，‎5‎，‎6‎，投这个骰子，掷的点数大于‎4‎的概率是________． ‎ ‎ ‎ ‎ 一个正多边形的每个内角度数均为‎135‎‎∘‎，则它的边数为________． ‎ ‎ ‎ ‎ 代数式‎3x−1‎x−2‎的值为‎2‎，则x＝________． ‎ ‎ ‎ ‎ 某快递公司每天上午‎9:30−10:30‎为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，该时段内甲、乙两仓库的快件数量y（件）与时间x（分）之间的函数图象如图所示，那么从‎9:30‎开始，经过________分钟时，当两仓库快递件数相同． ‎ ‎ ‎ ‎ 如图，矩形ABCD中，AB＝‎8‎，BC＝‎12‎，E为AD中点，F为AB上一点，将‎△AEF沿EF折叠后，点A恰好落到CF上的点G处，则折痕EF的长是________． ‎ 三、解答题（本大题共9小题，共78分）‎ ‎ ‎ ‎ 计算：‎(‎3‎‎)‎‎−1‎+‎3‎‎−8‎−sin‎60‎‎∘‎+(π−1‎‎)‎‎0‎． ‎ ‎ ‎ ‎ 解不等式组x−1<5‎x+4≥‎‎3x+7‎‎2‎‎ ‎ ‎ ‎ ‎ 第25页 共28页 ◎ 第26页 共28页 ‎ 已知：如图，在▱ABCD中，点E、F是对角线AC上的两点，且AE‎=‎CF．求证：BF // DE． ‎ ‎ ‎ ‎ 甲、乙两人加工同一种零件，甲每天加工的数量是乙每天加工数量的‎1.5‎倍，两人各加工‎300‎个这种零件，甲比乙少用‎5‎天． ‎ ‎（1）求甲、乙两人每天各加工多少个这种零件？‎ ‎ ‎ ‎（2）已知甲、乙两人加工这种零件每天的加工费分别是‎150‎元和‎120‎元，现有‎1500‎个这种零件的加工任务，甲单独加工一段时间后另有安排，剩余任务由乙单独完成．如果总加工费为‎7800‎元，那么甲乙各加工了多少天？‎ ‎ ‎ ‎ 如图，AC是‎⊙O的直径，AB是‎⊙O的一条弦，AP是‎⊙O的切线．作BM‎=AB并与AP交于点M，延长MB交AC于点E，交‎⊙O于点D，连接AD、BC． ‎ ‎(1)‎求证：AB‎=BE；‎ ‎ ‎ ‎(2)‎若BE=3‎，OC=‎‎5‎‎2‎，求BC的长．‎ ‎ ‎ ‎ 某校计划组织学生参加“书法”、“摄影”、“航模、“围棋”四个课外兴趣小组，要求每人必须参加，并且只能选择其中一个小组，为了解学生对四个课外兴趣小组的选择情况，学校从全体学生中随机抽取部分学生进行问卷调查，并把调查结果制成如图所示的扇形统计图和条形统计图（部分信息未给出），请你根据给出的信息解答下列问题： ‎ ‎（1）求参加这次问卷调查的学生人数，并补全条形统计图（画图后请标注相应的数据）；‎ ‎ ‎ ‎（2）m＝________，n＝________；‎ ‎ ‎ ‎（3）若该校共有‎1200‎名学生，试估计该校选择“围棋”课外兴趣小组的学生有多少人？‎ ‎ ‎ ‎（4）分别用A、B、C、D表示“书法”、“摄影”、“航模、“围棋”，小明和小红从中各选取一个小组，请用树状图法或列表法求出“两人选择小组不同”的概率．‎ ‎ ‎ ‎ 如图，已知一次函数y=‎5‎‎2‎x−2‎与反比例函数y=‎kx的图象相交于点A(2, n)‎，与x轴相交于点B． ‎ ‎（1）求k的值以及点B的坐标；‎ ‎ ‎ ‎（2）以AB为边作菱形ABCD，使点C在x轴正半轴上，点D在第一象限，求点D的坐标；‎ ‎ ‎ ‎（3）在y轴上是否存在点P，使PA+PB的值最小？若存在，请求出点P的坐标；若不存在，请说明理由．‎ ‎ ‎ ‎ ‎△ABC和‎△CDE都是等腰三角形，‎∠BAC＝‎∠EDC＝‎120‎‎∘‎． ‎ ‎（1）如图‎1‎，A、D、C在同一直线上时，ACBC‎=‎________，ADBE‎=‎________．‎ ‎ ‎ ‎（2）在图‎1‎的基础上，固定‎△ABC，将‎△CDE绕C旋转一定的角度α(‎0‎‎∘‎<α<‎360‎‎∘‎)‎，如图‎2‎，连接AD、BE． ①ADBE的值有没有改变？请说明理由． ②拓展研究：若AB＝‎1‎，DE=‎‎2‎，当B、D、E在同一直线上时，请计算线段AD的长．‎ 第25页 共28页 ◎ 第26页 共28页 ‎ ‎ ‎ 如图所示，在平面直角坐标系中，二次函数y＝ax‎2‎+bx+6(a≠0)‎交x轴于A(−4, 0)‎，B(2, 0)‎，在y轴上有一点E(0, −2)‎，连接AE． ‎ ‎（1）求二次函数的表达式；‎ ‎ ‎ ‎（2）点D是第二象限内的抛物线上一动点． ①求‎△ADE面积最大值并写出此时点D的坐标； ②若tan∠AED=‎‎1‎‎3‎，求此时点D坐标；‎ ‎ ‎ ‎（3）连接AC，点P是线段CA上的动点，连接OP，把线段PO绕着点P顺时针旋转‎90‎‎∘‎至PQ，点Q是点O的对应点．当动点P从点C运动到点A，则动点Q所经过的路径长等于________（直接写出答案）‎ 第25页 共28页 ◎ 第26页 共28页 参考答案与试题解析 ‎2020年山东省济南市槐荫区中考数学一模试卷 一、选择题（本大题共12个小题，每小题4分，共48分.在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1.‎ ‎【答案】‎ B ‎【考点】‎ 算术平方根 ‎【解析】‎ 如果一个非负数x的平方等于a，那么x是a的算术平方根，根据此定义即可求出结果．‎ ‎【解答】‎ ‎∵ ‎3‎‎2‎＝‎9‎， ∴ ‎9‎算术平方根为‎3‎．‎ ‎2.‎ ‎【答案】‎ C ‎【考点】‎ 简单组合体的三视图 ‎【解析】‎ 根据从左边看得到的图形是左视图，可得答案．‎ ‎【解答】‎ 从左边看第一层是两个小正方形，第二层左边一个小正方形，‎ ‎3.‎ ‎【答案】‎ C ‎【考点】‎ 科学记数法--表示较大的数 ‎【解析】‎ 科学记数法的表示形式为a×‎‎10‎n的形式，其中‎1≤|a|<10‎，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值‎>1‎时，n是正数；当原数的绝对值‎<1‎时，n是负数．‎ ‎【解答】‎ ‎62567‎用科学记数法表示‎6.2567×‎‎10‎‎4‎，‎ ‎4.‎ ‎【答案】‎ D ‎【考点】‎ 平行线的性质 ‎【解析】‎ 根据平行线的性质解答即可．‎ ‎【解答】‎ ‎∵ AB // CD， ∴ ‎∠1‎＝‎85‎‎∘‎， ∵ ‎∠E＝‎27‎‎∘‎， ∴ ‎∠D＝‎85‎‎∘‎‎−‎‎27‎‎∘‎＝‎58‎‎∘‎，‎ ‎5.‎ ‎【答案】‎ D ‎【考点】‎ 同底数幂的除法 单项式乘单项式 幂的乘方与积的乘方 合并同类项 ‎【解析】‎ 选项A为单项式‎×‎单项式；选项B为合并同类项；选项C为同底数幂的除法；选项D为积的乘方，根据相应的法则进行计算即可．‎ ‎【解答】‎ 选项A，单项式‎×‎单项式，‎(a‎3‎b)⋅(ab‎2‎)‎＝a‎3‎‎⋅a⋅b⋅‎b‎2‎＝a‎4‎b‎3‎，原计算正确，故此选项不符合题意； 选项B，合并同类项，xy‎2‎−‎1‎‎5‎xy‎2‎=‎5‎‎5‎xy‎2‎−‎1‎‎5‎xy‎2‎=‎4‎‎5‎xy‎2‎，原计算正确，故此选项不符合题意； 选项C，同底数幂的除法，a‎5‎‎÷‎a‎2‎＝a‎5−2‎＝a‎3‎，原计算正确，故此选项不符合题意； 选项D，积的乘方，‎(−mn‎3‎‎)‎‎2‎＝m‎2‎n‎6‎，原计算错误，故此选项符合题意；‎ ‎6.‎ ‎【答案】‎ B ‎【考点】‎ 中心对称图形 轴对称图形 ‎【解析】‎ 根据轴对称图形与中心对称图形的概念求解．‎ ‎【解答】‎ 解：A.不是轴对称图形，是中心对称图形，故本选项错误； B.是轴对称图形，不是中心对称图形，故本选项正确； C.既不是轴对称，也不是中心对称图形，故本选项错误； D.是轴对称图形，也是中心对称图形，故本选项错误． 故选B.‎ ‎7.‎ ‎【答案】‎ B 第25页 共28页 ◎ 第26页 共28页 ‎【考点】‎ 分式的加减运算 ‎【解析】‎ 先将后两项结合起来，然后再化成同分母分式，按照同分母分式加减的法则计算就可以了．‎ ‎【解答】‎ 原式‎=a‎2‎a−1‎−(a+1)‎， ‎=a‎2‎a−1‎−‎a‎2‎‎−1‎a−1‎， ‎=‎‎1‎a−1‎．‎ ‎8.‎ ‎【答案】‎ C ‎【考点】‎ 中位数 众数 ‎【解析】‎ 根据中位数和众数的定义分别进行解答即可．‎ ‎【解答】‎ 把这些数从小到大排列，中位数是第‎5‎和第‎6‎个数的平均数， 则中位数是‎97+98‎‎2‎‎=97.5‎（分）； ∵ ‎98‎出现了‎3‎次，出现的次数最多， ∴ 众数是‎98‎分；‎ ‎9.‎ ‎【答案】‎ C ‎【考点】‎ 反比例函数的图象 一次函数的图象 ‎【解析】‎ 根据题目中的函数解析式，利用分类讨论的方法可以判断各个选项中的函数图象是否正确，从而可以解答本题．‎ ‎【解答】‎ 当a<0‎时，函数y=‎ax在第二、四象限，一次函数y＝‎−ax+1‎经过一、二、三象限，故选项D错误（1）故选：C．‎ ‎10.‎ ‎【答案】‎ B ‎【考点】‎ 圆周角定理 扇形面积的计算 ‎【解析】‎ 连接OB、OC，先利用同弧所对的圆周角等于所对的圆心角的一半，求出扇形的圆心角为‎60‎度，即可求出半径的长‎1‎，利用三角形和扇形的面积公式即可求解；‎ ‎【解答】‎ 作OD⊥BC，则BD＝CD，连接OA，OB，OC， ∴ OD是BC的垂直平分线 ∴ AB‎=‎AC， ∴ AB＝AC， ∴ A在BC的垂直平分线上， ∴ A、O、D共线， ∵ ‎∠ACB＝‎75‎‎∘‎，AB＝AC， ∴ ‎∠ABC＝‎∠ACB＝‎75‎‎∘‎， ∴ ‎∠BAC＝‎30‎‎∘‎， ∴ ‎∠BOC＝‎60‎‎∘‎， ∵ OB＝OC， ∴ ‎△BOC是等边三角形， ∴ OA＝OB＝OC＝BC＝‎1‎， ∵ AD⊥BC，AB＝AC， ∴ BD＝CD， ∴ OD=‎3‎‎2‎OB=‎‎3‎‎2‎， ∴ AD＝‎1+‎‎3‎‎2‎， ∴ S‎△ABC‎=‎1‎‎2‎BC⋅AD=‎1‎‎2‎+‎‎3‎‎4‎， S‎△BOC‎=‎1‎‎2‎BC⋅OD=‎‎3‎‎4‎， ∴ S阴影＝S‎△ABC‎+S扇形BOC−S‎△BOC=‎1‎‎2‎+‎3‎‎4‎+‎60π×‎‎1‎‎2‎‎360‎−‎3‎‎4‎=‎1‎‎2‎+‎1‎‎6‎π，‎ ‎11.‎ ‎【答案】‎ A ‎【考点】‎ 解直角三角形的应用-坡度坡角问题 解直角三角形的应用-仰角俯角问题 ‎【解析】‎ 过点B作BM⊥EA的延长线于点M，过点B作BN⊥CE于点N，通过解直角三角形可求出BM，AM，CN，DE的长，再结合CD＝CN+EN−DE即可求出结论．‎ ‎【解答】‎ 第25页 共28页 ◎ 第26页 共28页 过点B作BM⊥EA的延长线于点M，过点B作BN⊥CE于点N，如图所示． 在Rt△ABM中，AB＝‎10‎米，‎∠BAM＝‎30‎‎∘‎， ∴ AM＝AB⋅cos∠BAM＝‎5‎‎3‎米，BM＝AB⋅sin∠BAM＝‎5‎米． 在Rt△ADE中，AE＝‎10‎米，‎∠DAE＝‎60‎‎∘‎， ∴ DE＝AE⋅tan∠DAE＝‎10‎‎3‎米． 在Rt△BCN中，BN＝AE+AM＝‎(10+5‎3‎)‎米，‎∠CBN＝‎45‎‎∘‎， ∴ CN＝BN⋅tan∠CBN＝‎(10+5‎3‎)‎米， ∴ CD＝CN+EN−DE＝‎10+5‎3‎+5−10‎3‎=(15−5‎3‎)‎米．‎ ‎12.‎ ‎【答案】‎ B ‎【考点】‎ 抛物线与x轴的交点 根的判别式 二次函数图象与系数的关系 ‎【解析】‎ 利用抛物线的对称性得到抛物线与x轴的另一个交点在点‎(−2, 0)‎和‎(−1, 0)‎之间，则当x＝‎−2‎时，y<0‎，于是可对①进行判断； 利用抛物线的对称轴为直线x=−b‎2a=1‎，即b＝‎−2a，则可对②进行判断； 利用抛物线的顶点的纵坐标为n得到‎4ac−‎b‎2‎‎4a‎=n，则可对③进行判断； 由于抛物线与直线y＝n有一个公共点，则抛物线与直线y＝n−1‎有‎2‎个公共点，于是可对④进行判断．‎ ‎【解答】‎ ‎①∵ 抛物线与x轴的一个交点在点‎(3, 0)‎和‎(4, 0)‎之间，而抛物线的对称轴为直线x＝‎1‎， ∴ 抛物线与x轴的另一个交点在点‎(−2, 0)‎和‎(−1, 0)‎之间． ∴ 当x＝‎−2‎时，y<0‎， 即‎4a−2b+c<0‎，所以①不符合题意； ②∵ 抛物线的对称轴为直线x=−b‎2a=1‎，即b＝‎−2a， ∴ ‎3a+b＝‎3a−2a＝a，所以②不符合题意； ③∵ 抛物线的顶点坐标为‎(1, n)‎， ∴ ‎4ac−‎b‎2‎‎4a‎=n， ∴ b‎2‎＝‎4ac−4an＝‎4a(c−n)‎，所以③符合题意； ④∵ 抛物线与直线y＝n有一个公共点， ∴ 抛物线与直线y＝n−1‎有‎2‎个公共点， ∴ 一元二次方程ax‎2‎+bx+c＝n−1‎有两个不相等的实数根，所以④符合题意．‎ 二、填空题（本大题共6小题，每小题4分，共24分）‎ ‎【答案】‎ ‎(2+m)(2−m)‎ ‎【考点】‎ 因式分解-运用公式法 ‎【解析】‎ 原式利用平方差公式分解即可．‎ ‎【解答】‎ 原式＝‎(2+m)(2−m)‎，‎ ‎【答案】‎ ‎1‎‎3‎ ‎【考点】‎ 概率公式 ‎【解析】‎ 先求出点数大于‎4‎的数，再根据概率公式求解即可．‎ ‎【解答】‎ 解：∵ 在这‎6‎种情况中，掷的点数大于‎4‎的有‎2‎种结果， ∴ 掷的点数大于‎4‎的概率为‎2‎‎6‎‎=‎‎1‎‎3‎. 故答案为：‎1‎‎3‎.‎ ‎【答案】‎ ‎8‎ ‎【考点】‎ 多边形内角与外角 ‎【解析】‎ 根据正多边形的一个内角是‎135‎‎∘‎，则知该正多边形的一个外角为‎45‎‎∘‎，再根据多边形的外角之和为‎360‎‎∘‎，即可求出正多边形的边数．‎ ‎【解答】‎ ‎∵ 正多边形的一个内角是‎135‎‎∘‎， ∴ 该正多边形的一个外角为‎45‎‎∘‎， ∵ 多边形的外角之和为‎360‎‎∘‎， ∴ 边数n=‎360‎‎45‎=8‎， ∴ 该正多边形为正八边形，‎ ‎【答案】‎ ‎−3‎ ‎【考点】‎ 解分式方程 ‎【解析】‎ 根据分式方程的解法即可求出答案．‎ ‎【解答】‎ 由题意可知：‎3x−1‎x−2‎‎=2‎， 解得：x＝‎−3‎， 经检验，x＝‎−3‎是方程的解 ‎【答案】‎ ‎20‎ ‎【考点】‎ 一次函数的应用 ‎【解析】‎ 分别求出甲、乙两仓库的快件数量y（件）与时间x（分）之间的函数关系式，求出两条直线的交点坐标即可．‎ ‎【解答】‎ 设甲仓库的快件数量y（件）与时间x（分）之间的函数关系式为：y‎1‎＝k‎1‎x+40‎，根据题意得‎60k‎1‎+40‎＝‎400‎，解得k‎1‎＝‎6‎， ∴ y‎1‎＝‎6x+40‎； 设乙仓库的快件数量y（件）与时间x（分）之间的函数关系式为：y‎2‎＝k‎2‎x+240‎，根据题意得‎60k‎2‎+240‎＝‎0‎，解得k‎2‎＝‎−4‎， ∴ y‎2‎＝‎−4x+240‎， 联立y=6x+40‎y=−4x+240‎‎ ‎， 解得 第25页 共28页 ◎ 第26页 共28页 x=20‎y=160‎‎ ‎‎， ∴ 经过‎20‎分钟时，当两仓库快递件数相同．‎ ‎【答案】‎ ‎15‎‎2‎ ‎【考点】‎ 矩形的性质 翻折变换（折叠问题）‎ ‎【解析】‎ 连接EC，利用矩形的性质，求出EG，DE的长度，证明EC平分‎∠DCF，再证‎∠FEC＝‎90‎‎∘‎，最后证‎△FEC∽△EDC，利用相似的性质即可求出EF的长度．‎ ‎【解答】‎ 如图，连接EC， ∵ 四边形ABCD为矩形， ∴ ‎∠A＝‎∠D＝‎90‎‎∘‎，BC＝AD＝‎12‎，DC＝AB＝‎8‎， ∵ E为AD中点， ∴ AE＝DE=‎1‎‎2‎AD＝‎6‎， 由翻折知，‎△AEF≅△GEF， ∴ AE＝GE＝‎6‎，‎∠AEF＝‎∠GEF，‎∠EGF＝‎∠EAF＝‎90‎‎∘‎＝‎∠D， ∴ GE＝DE， ∴ EC平分‎∠DCG， ∴ ‎∠DCE＝‎∠GCE， ∵ ‎∠GEC＝‎90‎‎∘‎‎−∠GCE，‎∠DEC＝‎90‎‎∘‎‎−∠DCE， ∴ ‎∠GEC＝‎∠DEC， ∴ ‎∠FEC＝‎∠FEG+∠GEC=‎1‎‎2‎×‎‎180‎‎∘‎＝‎90‎‎∘‎， ∴ ‎∠FEC＝‎∠D＝‎90‎‎∘‎， 又∵ ‎∠DCE＝‎∠GCE， ∴ ‎△FEC∽△EDC， ∴ EFDE‎=‎ECDC， ∵ EC=DE‎2‎+DC‎​‎‎2‎‎6‎​‎‎2‎+8‎‎​‎‎2‎=10‎， ∴ EF‎6‎‎=‎‎10‎‎8‎， ∴ FE=‎‎15‎‎2‎，‎ 三、解答题（本大题共9小题，共78分）‎ ‎【答案】‎ 原式‎=‎1‎‎3‎+(−2)−‎3‎‎2‎+1‎ ‎=‎3‎‎3‎−2−‎3‎‎2‎+1‎ ‎‎=−‎3‎‎6‎−1‎ ‎【考点】‎ 零指数幂、负整数指数幂 零指数幂 特殊角的三角函数值 实数的运算 ‎【解析】‎ 按照负整数指数幂、立方根、锐角三角函数值、零指数幂意义解题即可．‎ ‎【解答】‎ 原式‎=‎1‎‎3‎+(−2)−‎3‎‎2‎+1‎ ‎=‎3‎‎3‎−2−‎3‎‎2‎+1‎ ‎‎=−‎3‎‎6‎−1‎ ‎【答案】‎ 解不等式x−1<5‎，得：x<6‎； 解不等式x+4≥‎‎3x+7‎‎2‎，得：x≤1‎， 则不等式组的解集为x≤1‎．‎ ‎【考点】‎ 解一元一次不等式组 ‎【解析】‎ 分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．‎ ‎【解答】‎ 解不等式x−1<5‎，得：x<6‎； 解不等式x+4≥‎‎3x+7‎‎2‎，得：x≤1‎， 则不等式组的解集为x≤1‎．‎ ‎【答案】‎ 第25页 共28页 ◎ 第26页 共28页 证明：∵ 四边形ABCD是平行四边形， ∴ AD‎=‎BC，AD // BC， ∴ ‎∠DAE‎=‎‎∠BCF， 又∵ AE‎=‎CF， 在‎△ADE与‎△CBF中 AD=BC，‎‎∠DAE=∠BCF，‎AE=CF，‎‎ ‎ ∴ ‎△ADE≅△CBF(SAS)‎， ∴ ‎∠AED‎=‎‎∠CFB， ∴ ‎∠DEC‎=‎‎∠BFA， ∴ DE // BF.‎ ‎【考点】‎ 全等三角形的性质与判定 平行四边形的性质 ‎【解析】‎ 可由题中条件求解‎△ADE≅△CBF，得出‎∠AED＝‎∠CFB，即‎∠DEC‎=‎‎∠BFA，进而可求证DE与BF平行．‎ ‎【解答】‎ 证明：∵ 四边形ABCD是平行四边形， ‎ ‎∴ AD‎=‎BC，AD // BC，‎ ‎∴ ‎∠DAE‎=‎‎∠BCF，‎ 又∵ AE‎=‎CF，‎ 在‎△ADE与‎△CBF中 AD=BC，‎‎∠DAE=∠BCF，‎AE=CF，‎‎ ‎ ‎∴ ‎△ADE≅△CBF(SAS)‎，‎ ‎∴ ‎∠AED‎=‎‎∠CFB，‎ ‎∴ ‎∠DEC‎=‎‎∠BFA，‎ ‎∴ DE // BF.‎ ‎【答案】‎ 甲、乙两人每天各加工‎30‎和‎20‎个这种零件 甲乙各加工了‎40‎天和‎15‎天 ‎【考点】‎ 分式方程的应用 ‎【解析】‎ ‎（1）设乙每天加工x个零件，则甲每天加工‎1.5x个零件，根据题意列出方程即可求出答案． （2）设甲乙各加工了m和n天，根据题意列出方程组即可求出答案．‎ ‎【解答】‎ 设乙每天加工x个零件， 则甲每天加工‎1.5x个零件， ∴ ‎300‎‎1.5x‎=‎300‎x−5‎， 解得：x＝‎20‎， 经检验，x＝‎20‎是原方程的解， ∴ ‎1.5x＝‎30‎， 答：甲、乙两人每天各加工‎30‎和‎20‎个这种零件．‎ 设甲乙各加工了m和n天， ‎30m+20n=1500‎‎150m+120n=7800‎‎ ‎， 解得：m=40‎n=15‎‎ ‎， 答：甲乙各加工了‎40‎天和‎15‎天．‎ ‎【答案】‎ ‎(1)‎证明：∵ AP是‎⊙O的切线， ∴ ‎∠EAM‎=‎‎90‎‎∘‎， ∴ ‎∠BAE+∠MAB‎=‎‎90‎‎∘‎，‎∠AEB+∠AMB‎=‎‎90‎‎∘‎． 又∵ AB‎=BM， ∴ ‎∠MAB‎=∠AMB， ∴ ‎∠BAE‎=∠AEB， ∴ AB‎=BE；‎ ‎(2)‎解：∵ AC是‎⊙O的直径， ∴ ‎∠ABC‎=‎‎90‎‎∘‎， 在Rt△ABC中，AC‎=2OC=5‎，AB‎=BE=3‎， ∴ BC=4‎．‎ ‎【考点】‎ 圆周角定理 切线的性质 ‎【解析】‎ ‎（1）根据切线的性质得出‎∠EAM＝‎90‎‎∘‎，等腰三角形的性质‎∠MAB＝‎∠AMB，根据等角的余角相等得出‎∠BAE＝‎∠AEB，即可证得AB＝BE； （2）根据勾股定理即可得到结论．‎ ‎【解答】‎ ‎(1)‎证明：∵ AP是‎⊙O的切线， ∴ ‎∠EAM‎=‎‎90‎‎∘‎， ∴ ‎∠BAE+∠MAB‎=‎‎90‎‎∘‎，‎∠AEB+∠AMB‎=‎‎90‎‎∘‎． 又∵ AB‎=BM， ∴ ‎∠MAB‎=∠AMB， ∴ ‎∠BAE‎=∠AEB， ∴ AB‎=BE；‎ ‎(2)‎解：∵ AC是‎⊙O的直径， ∴ ‎∠ABC‎=‎‎90‎‎∘‎， 在Rt△ABC中，AC‎=2OC=5‎，AB‎=BE=3‎， ∴ BC=4‎．‎ ‎【答案】‎ 参加这次问卷调查的学生人数为：‎30÷20%‎＝‎150‎（人）， 航模的人数为‎150−(30+54+24)‎＝‎42‎（人）， 补全图形如下： ‎ ‎36‎‎,‎‎16‎ 第25页 共28页 ◎ 第26页 共28页 该校选择“围棋”课外兴趣小组的学生有‎1200×16%‎＝‎192‎（人）；‎ 根据题意画图如下： 共有‎16‎种等情况数，其中“两人选择小组不同”的有‎12‎种， 则“两人选择小组不同”的概率是‎12‎‎16‎‎=‎‎3‎‎4‎．‎ ‎【考点】‎ 列表法与树状图法 用样本估计总体 扇形统计图 条形统计图 ‎【解析】‎ ‎（1）由书法小组人数及其对应百分比可得总人数，再根据各小组人数之和等于总人数求得航模人数，从而补全图形； （2）根据百分比的概念可得m、n的值； （3）总人数乘以样本中围棋的人数所占百分比； （4）根据题意画出树状图得出所有等情况数和“两人选择小组不同”的情况数，再根据概率公式即可得出答案．‎ ‎【解答】‎ 参加这次问卷调查的学生人数为：‎30÷20%‎＝‎150‎（人）， 航模的人数为‎150−(30+54+24)‎＝‎42‎（人）， 补全图形如下： ‎ m%=‎54‎‎150‎×100%‎‎＝‎36%‎，n%=‎24‎‎150‎×100%‎＝‎16%‎， 即m＝‎36‎，n＝‎16‎， 故答案为：‎36‎、‎16‎；‎ 该校选择“围棋”课外兴趣小组的学生有‎1200×16%‎＝‎192‎（人）；‎ 根据题意画图如下： 共有‎16‎种等情况数，其中“两人选择小组不同”的有‎12‎种， 则“两人选择小组不同”的概率是‎12‎‎16‎‎=‎‎3‎‎4‎．‎ ‎【答案】‎ 把点A(2, n)‎代入一次函数y=‎5‎‎2‎x−2‎， 可得n=‎5‎‎2‎×2−2‎＝‎3‎； 把点A(2, 3)‎代入反比例函数y=‎kx， 可得k＝xy＝‎2×3‎＝‎6‎， ∵ 一次函数y=‎5‎‎2‎x−2‎与x轴相交于点B， ∴ ‎5‎‎2‎x−2‎＝‎0‎， 解得x=‎‎4‎‎5‎， ∴ 点B的坐标为‎(‎4‎‎5‎, 0)‎；‎ ‎∵ 点A(2, 3)‎，B(‎4‎‎5‎, 0)‎， ∴ AB=‎(2−‎4‎‎5‎‎)‎‎2‎+(3−0‎‎)‎‎2‎=‎261‎‎25‎=‎‎3‎‎29‎‎5‎， ∵ 四边形ABCD是菱形， ∴ AD＝AB=‎‎3‎‎29‎‎5‎，AD // BC， ∵ 点C在x轴正半轴上，点D在第一象限， ∴ D(2+‎3‎‎29‎‎5‎, 3)‎；‎ 存在， 如图，作点B(‎4‎‎5‎, 0)‎关于y轴的对称点Q的坐标为‎(−‎4‎‎5‎, 0)‎，连接AQ交y轴于点P，此时PA+PB的值最小， 设直线AQ的解析式为：y＝kx+b， 则‎−‎4‎‎5‎k+b=0‎‎2k+b=3‎‎ ‎，解得：k=‎‎15‎‎14‎b=‎‎6‎‎7‎‎ ‎， ∴ 直线AQ的关系式为y=‎15‎‎14‎x+‎‎6‎‎7‎， ∴ 直线AQ与 第25页 共28页 ◎ 第26页 共28页 y轴的交点为P(0, ‎6‎‎7‎)‎．‎ ‎【考点】‎ 反比例函数综合题 ‎【解析】‎ ‎（1）把A点坐标代入一次函数解析式可求得n，则可求得A点坐标，代入反比例函数解析式则可求得k的值，最后根据y＝‎0‎可得点B的坐标 （2）根据两点的距离公式可得AB的长，由菱形的边长相等可得AD＝AB，根据AD与BC平行，可知A与D的纵坐标相等，由此可得D的坐标； （3）作点B(‎4‎‎5‎, 0)‎关于y轴的对称点Q的坐标为‎(−‎4‎‎5‎, 0)‎，连接AQ交y轴的交点为P，求出AQ解析式即可求解．‎ ‎【解答】‎ 把点A(2, n)‎代入一次函数y=‎5‎‎2‎x−2‎， 可得n=‎5‎‎2‎×2−2‎＝‎3‎； 把点A(2, 3)‎代入反比例函数y=‎kx， 可得k＝xy＝‎2×3‎＝‎6‎， ∵ 一次函数y=‎5‎‎2‎x−2‎与x轴相交于点B， ∴ ‎5‎‎2‎x−2‎＝‎0‎， 解得x=‎‎4‎‎5‎， ∴ 点B的坐标为‎(‎4‎‎5‎, 0)‎；‎ ‎∵ 点A(2, 3)‎，B(‎4‎‎5‎, 0)‎， ∴ AB=‎(2−‎4‎‎5‎‎)‎‎2‎+(3−0‎‎)‎‎2‎=‎261‎‎25‎=‎‎3‎‎29‎‎5‎， ∵ 四边形ABCD是菱形， ∴ AD＝AB=‎‎3‎‎29‎‎5‎，AD // BC， ∵ 点C在x轴正半轴上，点D在第一象限， ∴ D(2+‎3‎‎29‎‎5‎, 3)‎；‎ 存在， 如图，作点B(‎4‎‎5‎, 0)‎关于y轴的对称点Q的坐标为‎(−‎4‎‎5‎, 0)‎，连接AQ交y轴于点P，此时PA+PB的值最小， 设直线AQ的解析式为：y＝kx+b， 则‎−‎4‎‎5‎k+b=0‎‎2k+b=3‎‎ ‎，解得：k=‎‎15‎‎14‎b=‎‎6‎‎7‎‎ ‎， ∴ 直线AQ的关系式为y=‎15‎‎14‎x+‎‎6‎‎7‎， ∴ 直线AQ与y轴的交点为P(0, ‎6‎‎7‎)‎．‎ ‎【答案】‎ ‎3‎‎3‎‎,‎‎3‎‎3‎ 第25页 共28页 ◎ 第26页 共28页 ‎①没有改变， 理由如下：∵ 将‎△CDE绕C旋转一定的角度α(‎0‎‎∘‎<α<‎360‎‎∘‎)‎， ∴ ‎∠ACD＝‎∠BCE， ∵ AB＝AC，DE＝CD， ∴ ACCD‎=‎ABDE，且‎∠BAC＝‎∠EDC＝‎120‎‎∘‎， ∴ ‎△ABC∽△DEC， ∴ BCEC‎=‎ACCD，且‎∠ACD＝‎∠BCE， ∴ ‎△ACD∽△BCE， ∴ ADBE‎=ACBC=‎‎3‎‎3‎； ②如图‎2‎，当B、D、E在同一直线上时，过点C作CN⊥BE于N，连接AD， ∵ AC＝AB＝‎1‎， ∴ BC=‎‎3‎， ∵ ‎∠CDE＝‎120‎‎∘‎， ∴ ‎∠BDC＝‎60‎‎∘‎，且CD＝DE=‎‎2‎，CN⊥BE， ∴ DN=‎1‎‎2‎CD=‎‎2‎‎2‎，CN=‎3‎DN=‎‎6‎‎2‎ ∵ BN=BC‎2‎−CN‎2‎=‎3−‎‎3‎‎2‎=‎‎6‎‎2‎， ∴ BE=‎6‎‎2‎+‎‎3‎‎2‎‎2‎， ∵ ADBE‎=‎‎3‎‎3‎， ∴ AD=‎‎2‎‎+‎‎6‎‎2‎．‎ ‎【考点】‎ 几何变换综合题 ‎【解析】‎ ‎（1）由等腰三角形的性质和直角三角形的性质可得AC＝‎2AH，CH=‎3‎AH，由平行线分线段成比例可得ADBE‎=ACBC=‎2AH‎2‎3‎AH=‎‎3‎‎3‎，即可求解； （2）①证明‎△ACD∽△BCE，可得ADBE‎=ACBC=‎‎3‎‎3‎； ②过点C作CN⊥BE于N，连接AD，利用直角三角形的性质和勾股定理求出BE=‎6‎‎2‎+‎‎3‎‎2‎‎2‎，由①的结论可求解．‎ ‎【解答】‎ 如图‎1‎，过点A作AH⊥BC于H， ∵ ‎∠BAC＝‎120‎‎∘‎，AB＝AC，AH⊥BC， ∴ ‎∠ABC＝‎∠ACB＝‎30‎‎∘‎，BH＝CH， ∴ AC＝‎2AH，CH=‎3‎AH， ∴ BC＝‎2‎3‎AH， ∵ ‎∠BAC＝‎∠EDC＝‎120‎‎∘‎， ∴ AB // DE， ∴ ADBE‎=ACBC=‎2AH‎2‎3‎AH=‎‎3‎‎3‎， 故答案为：‎3‎‎3‎，‎3‎‎3‎；‎ ‎①没有改变， 理由如下：∵ 将‎△CDE绕C旋转一定的角度α(‎0‎‎∘‎<α<‎360‎‎∘‎)‎， ∴ ‎∠ACD＝‎∠BCE， ∵ AB＝AC，DE＝CD， ∴ ACCD‎=‎ABDE，且‎∠BAC＝‎∠EDC＝‎120‎‎∘‎， ∴ ‎△ABC∽△DEC， ∴ BCEC‎=‎ACCD，且‎∠ACD＝‎∠BCE， ∴ ‎△ACD∽△BCE， ∴ ADBE‎=ACBC=‎‎3‎‎3‎； ②如图‎2‎，当B、D、E在同一直线上时，过点C作CN⊥BE于N，连接AD， ∵ AC＝AB＝‎1‎， ∴ BC=‎‎3‎， ∵ ‎∠CDE＝‎120‎‎∘‎， ∴ ‎∠BDC＝‎60‎‎∘‎，且CD＝DE=‎‎2‎，CN⊥BE， ∴ DN=‎1‎‎2‎CD=‎‎2‎‎2‎，CN=‎3‎DN=‎‎6‎‎2‎ ∵ BN=BC‎2‎−CN‎2‎=‎3−‎‎3‎‎2‎=‎‎6‎‎2‎， ∴ BE=‎6‎‎2‎+‎‎3‎‎2‎‎2‎， ∵ ADBE‎=‎‎3‎‎3‎， ∴ AD=‎‎2‎‎+‎‎6‎‎2‎．‎ ‎【答案】‎ 将A(−4, 0)‎，B(2, 0)‎代入y＝ax‎2‎+bx+6(a≠0)‎， 可得a=−‎‎3‎‎4‎，b=−‎‎3‎‎2‎， ∴ y=−‎3‎‎4‎x‎2‎−‎3‎‎2‎x+6‎；‎ ‎①∵ A(−4, 0)‎，E(0, −2)‎， 设D(m, −‎3‎‎4‎m‎2‎−‎3‎‎2‎m+6)‎， 过点D作DK⊥y轴交于点K； K(0, −‎3‎‎4‎m‎2‎−‎3‎‎2‎m+6)‎， S‎△ADE＝S梯形DKOA‎+S‎△AOE−‎S‎△KED ‎=‎1‎‎2‎×(KD+AO)×OK+‎1‎‎2‎×AO×OE−‎1‎‎2‎×KD×KE ‎=‎1‎‎2‎(−m+4)×(−‎3‎‎4‎m‎2‎−‎3‎‎2‎m+6)+‎1‎‎2‎×4×2−‎1‎‎2‎×(−m)×(2−‎3‎‎4‎m‎2‎−‎3‎‎2‎m+6)‎ ‎=−‎3‎‎2‎(m+‎2‎‎3‎‎)‎‎2‎+‎‎50‎‎3‎， 当m=−‎‎2‎‎3‎时，S‎△ADE的面积最大，最大值为‎50‎‎3‎； ②过点A作AN⊥DE，DE与x轴交于点F， ∵ tan∠AED=‎‎1‎‎3‎， ‎ 第25页 共28页 ◎ 第26页 共28页 ‎∴ AN=‎‎2‎，NE＝‎3‎‎2‎， Rt△AFN∽Rt△EFO， ∴ ANOE‎=‎NFOF， ∵ EF‎2‎＝OF‎2‎+4‎， ∴ NF＝‎3‎2‎−EF， ∴ ‎2‎‎2‎‎=‎‎3‎2‎−‎‎4+OF‎2‎OF， ∴ OF＝‎2‎， ∴ F(−2, 0)‎， ∴ EF直线解析式为y＝‎−x−2‎， ∴ ‎−x−2=−‎3‎‎4‎x‎2‎−‎3‎‎2‎x+6‎时，x=‎‎−1−‎‎97‎‎3‎， ∴ D(‎−1−‎‎97‎‎3‎, ‎−5+‎‎97‎‎3‎)‎；‎ ‎2‎‎26‎ ‎【考点】‎ 二次函数综合题 ‎【解析】‎ ‎（1）将A(−4, 0)‎，B(2, 0)‎代入y＝ax‎2‎+bx+6(a≠0)‎，求得y=−‎3‎‎4‎x‎2‎−‎3‎‎2‎x+6‎； （2）①由已知可求：AE＝‎2‎‎5‎，AE的直线解析式y=−‎1‎‎2‎x−2‎，设D(m, −‎3‎‎4‎m‎2‎−‎3‎‎2‎m+6)‎，过点D作DK⊥y轴交于点K；K(0, −‎3‎‎4‎m‎2‎−‎3‎‎2‎m+6)‎，S‎△ADE＝S梯形DKOA‎+S‎△AOE−S‎△KED=−‎3‎‎2‎(m+‎2‎‎3‎‎)‎‎2‎+‎‎50‎‎3‎； ②过点A作AN⊥DE，DE与x中交于点F，由tan∠AED=‎‎1‎‎3‎，可求AN=‎‎2‎，NE＝‎3‎‎2‎，因为Rt△AFN∽Rt△EFO，ANOE‎=‎NFOF，则有‎2‎‎2‎‎=‎‎3‎2‎−‎‎4+OF‎2‎OF，所以F(−2, 0)‎，得到EF直线解析式为y＝‎−x−2‎，直线与抛物线的交点为D点； （3）由于Q点随P点运动而运动，P点在线段AC上运动，所以Q点的运动轨迹是线段，当P点在A点时，Q(−4, −4)‎，当P点在C点时，Q(−6, 6)‎，Q点的轨迹长为‎2‎‎26‎．‎ ‎【解答】‎ 将A(−4, 0)‎，B(2, 0)‎代入y＝ax‎2‎+bx+6(a≠0)‎， 可得a=−‎‎3‎‎4‎，b=−‎‎3‎‎2‎， ∴ y=−‎3‎‎4‎x‎2‎−‎3‎‎2‎x+6‎；‎ ‎①∵ A(−4, 0)‎，E(0, −2)‎， 设D(m, −‎3‎‎4‎m‎2‎−‎3‎‎2‎m+6)‎， 过点D作DK⊥y轴交于点K； K(0, −‎3‎‎4‎m‎2‎−‎3‎‎2‎m+6)‎， S‎△ADE＝S梯形DKOA‎+S‎△AOE−‎S‎△KED ‎=‎1‎‎2‎×(KD+AO)×OK+‎1‎‎2‎×AO×OE−‎1‎‎2‎×KD×KE ‎=‎1‎‎2‎(−m+4)×(−‎3‎‎4‎m‎2‎−‎3‎‎2‎m+6)+‎1‎‎2‎×4×2−‎1‎‎2‎×(−m)×(2−‎3‎‎4‎m‎2‎−‎3‎‎2‎m+6)‎ ‎=−‎3‎‎2‎(m+‎2‎‎3‎‎)‎‎2‎+‎‎50‎‎3‎， 当m=−‎‎2‎‎3‎时，S‎△ADE的面积最大，最大值为‎50‎‎3‎； ②过点A作AN⊥DE，DE与x轴交于点F， ∵ tan∠AED=‎‎1‎‎3‎， ∴ AN=‎‎2‎，NE＝‎3‎‎2‎， Rt△AFN∽Rt△EFO， ∴ ANOE‎=‎NFOF， ∵ EF‎2‎＝OF‎2‎+4‎， ∴ NF＝‎3‎2‎−EF， ∴ ‎2‎‎2‎‎=‎‎3‎2‎−‎‎4+OF‎2‎OF， ∴ OF＝‎2‎， ∴ F(−2, 0)‎， ∴ EF直线解析式为y＝‎−x−2‎， ∴ ‎−x−2=−‎3‎‎4‎x‎2‎−‎3‎‎2‎x+6‎时，x=‎‎−1−‎‎97‎‎3‎， ∴ D(‎−1−‎‎97‎‎3‎, ‎−5+‎‎97‎‎3‎)‎；‎ 第25页 共28页 ◎ 第26页 共28页 ‎∵ Q点随P点运动而运动，P点在线段AC上运动， ∴ Q点的运动轨迹是线段， 当P点在A点时，Q(−4, −4)‎， 当P点在C点时，Q(−6, 6)‎， ∴ Q点的轨迹长为‎2‎‎26‎， 故答案为‎2‎‎26‎． ‎ 第25页 共28页 ◎ 第26页 共28页