2020九年级数学上册二次函数表达式的确定 6页

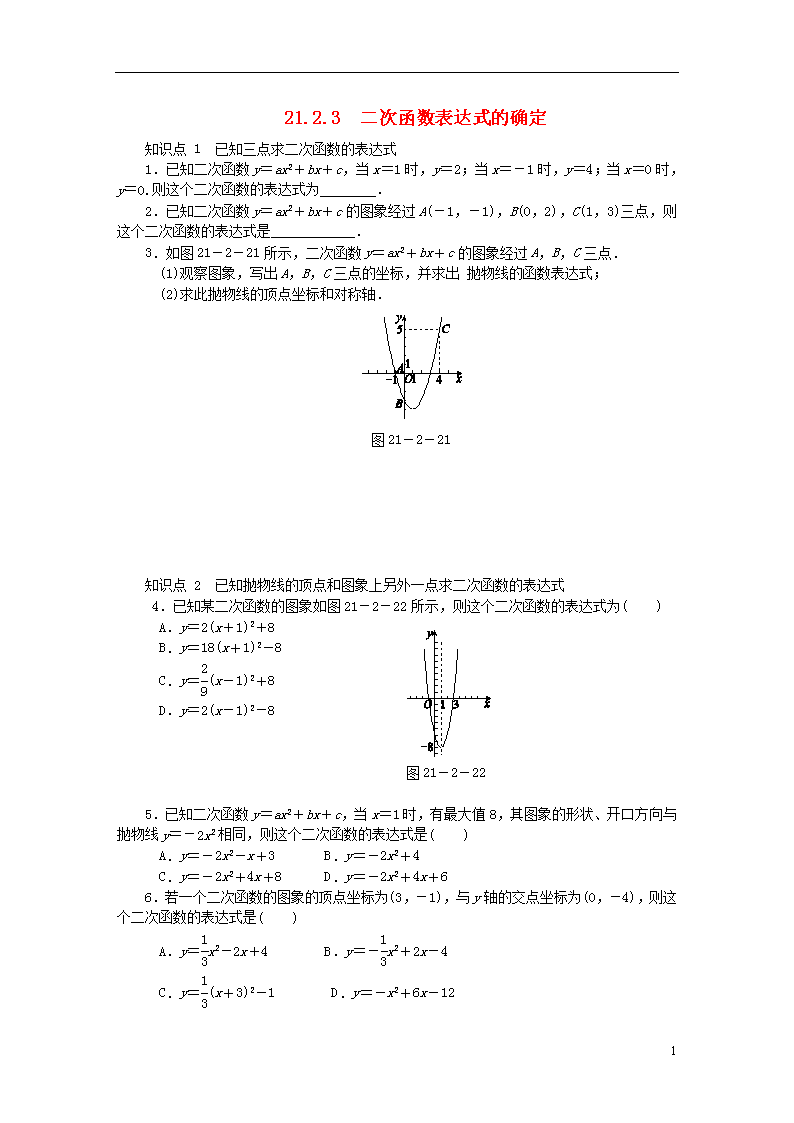
‎21.2.3　‎二次函数表达式的确定 知识点 1　已知三点求二次函数的表达式 ‎1．已知二次函数y＝ax2＋bx＋c，当x＝1时，y＝2；当x＝－1时，y＝4；当x＝0时，y＝0.则这个二次函数的表达式为________．‎ ‎2．已知二次函数y＝ax2＋bx＋c的图象经过A(－1，－1)，B(0，2)，C(1，3)三点，则这个二次函数的表达式是____________．‎ ‎3．如图21－2－21所示，二次函数y＝ax2＋bx＋c的图象经过A，B，C三点．‎ ‎(1)观察图象，写出A，B，C三点的坐标，并求出 抛物线的函数表达式；‎ ‎(2)求此抛物线的顶点坐标和对称轴．‎ 图21－2－21‎ 知识点 2　已知抛物线的顶点和图象上另外一点求二次函数的表达式 ‎ 4．已知某二次函数的图象如图21－2－22所示，则这个二次函数的表达式为(　　)‎ A．y＝2(x＋1)2＋8‎ B．y＝18(x＋1)2－8‎ C．y＝(x－1)2＋8‎ D．y＝2(x－1)2－8‎ ‎ 图21－2－22‎ ‎5．已知二次函数y＝ax2＋bx＋c，当x＝1时，有最大值8，其图象的形状、开口方向与抛物线y＝－2x2相同，则这个二次函数的表达式是(　　)‎ A．y＝－2x2－x＋3 B．y＝－2x2＋4‎ C．y＝－2x2＋4x＋8 D．y＝－2x2＋4x＋6‎ ‎6．若一个二次函数的图象的顶点坐标为(3，－1)，与y轴的交点坐标为(0，－4)，则这个二次函数的表达式是(　　)‎ A．y＝x2－2x＋4 B．y＝－x2＋2x－4‎ C．y＝(x＋3)2－1 D．y＝－x2＋6x－12‎ 6‎ ‎7．已知二次函数的图象过坐标原点，且顶点坐标是(1，－2)，则这个二次函数的表达式为__________．‎ ‎8．已知二次函数y＝ax2＋bx＋c中自变量x和函数值y的部分对应值如下表：‎ x ‎…‎ ‎－ ‎－1‎ ‎－ ‎0‎ ‎1‎ ‎…‎ y ‎…‎ ‎－ ‎－2‎ ‎－ ‎－2‎ ‎－ ‎0‎ ‎…‎ 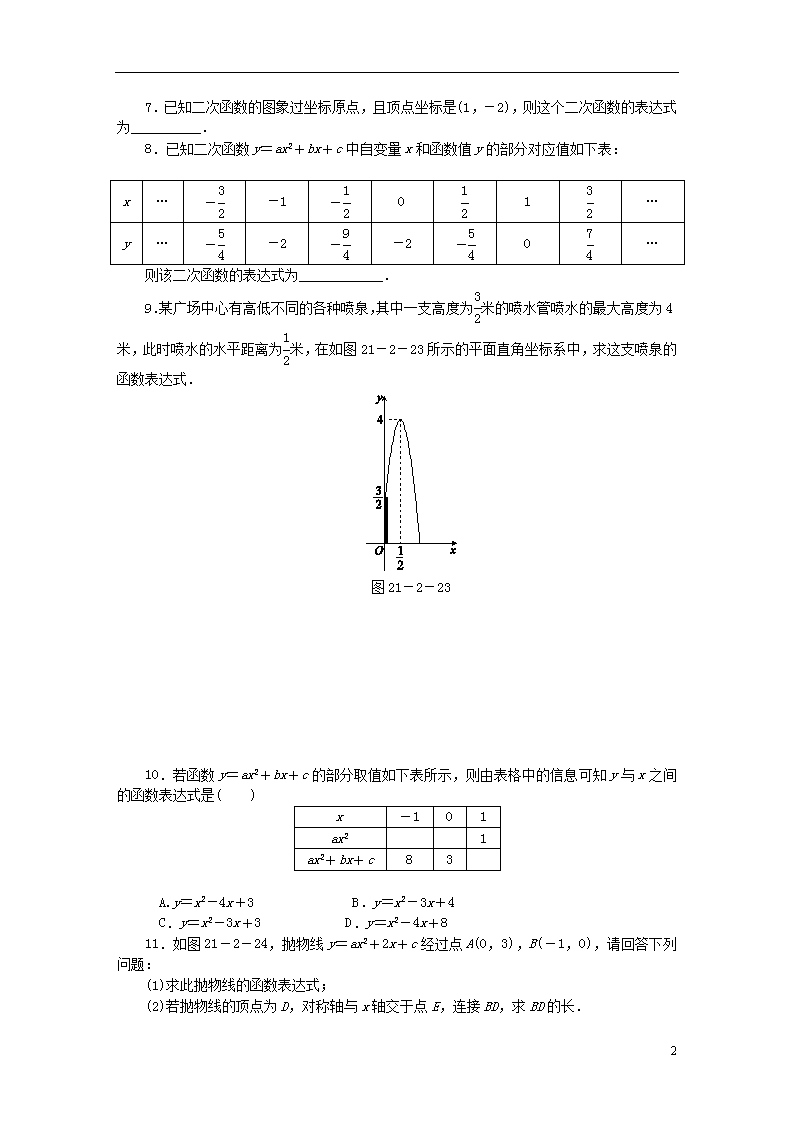则该二次函数的表达式为____________．‎ ‎9．某广场中心有高低不同的各种喷泉，其中一支高度为米的喷水管喷水的最大高度为‎4米，此时喷水的水平距离为米，在如图21－2－23所示的平面直角坐标系中，求这支喷泉的函数表达式．‎ 图21－2－23‎ ‎10．若函数y＝ax2＋bx＋c的部分取值如下表所示，则由表格中的信息可知y与x之间的函数表达式是(　　)‎ x ‎－1‎ ‎0‎ ‎1‎ ax2‎ ‎1‎ ax2＋bx＋c ‎8‎ ‎3‎ A.y＝x2－4x＋3 B．y＝x2－3x＋4‎ C．y＝x2－3x＋3 D．y＝x2－4x＋8‎ ‎11．如图21－2－24，抛物线y＝ax2＋2x＋c经过点A(0，3)，B(－1，0)，请回答下列问题：‎ ‎(1)求此抛物线的函数表达式；‎ ‎(2)若抛物线的顶点为D，对称轴与x轴交于点E，连接BD，求BD的长．‎ 6‎ 图21－2－24‎ ‎12．如图21－2－25，直线y＝x＋2与x轴交于点A，与y轴交于点B，AB⊥BC，且点C在x轴上．若抛物线y＝ax2＋bx＋c以C为顶点，且经过点B，求这条抛物线的表达式．‎ 图21－2－25‎ ‎13．［2016·娄底］如图21－2－26，抛物线y＝ax2＋bx＋c(a，b，c为常数，a≠0)经过点A(－1，0)，B(5，－6)，C(6，0)．‎ ‎(1)求抛物线的表达式．‎ ‎(2)在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大？若存在，‎ 6‎ 请求出点P的坐标；若不存在，请说明理由．‎ 图21－2－26‎ ‎14．已知抛物线l：y＝ax2＋bx＋c(a，b，c均不为0)的顶点为M，与y轴的交点为N.我们称以N为顶点，对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线，直线MN为抛物线l的衍生直线．‎ ‎(1)抛物线y＝x2－2x－3的衍生抛物线的表达式是____________，衍生直线的表达式是____________；‎ ‎(2)若一条抛物线的衍生抛物线和衍生直线分别是y＝－2x2＋1和y＝－2x＋1，求这条抛物线的表达式．‎ 6‎ ‎1．y＝3x2－x　2．y＝－x2＋2x＋2‎ ‎3．解：(1)A(－1，0)，B(0，－3)，C(4，5)，函数表达式为y＝x2－2x－3.‎ ‎(2)抛物线顶点坐标为(1，－4)，对称轴为直线x＝1.‎ ‎4．D　[解析] 由题图知抛物线的顶点坐标是(1，－8)，所以设抛物线的表达式是y＝a(x－1)2－8.因为点(3，0)在这个二次函数的图象上，所以0＝a×(3－1)2－8，解得a＝2.所以这个二次函数的表达式为y＝2(x－1)2－8.‎ ‎5．D ‎6．B　[解析] 设抛物线的表达式为y＝a(x－3)2－1，把(0，－4)代入，得a×(－3)2－1＝－4，解得a＝－，所以抛物线的表达式为y＝－(x－3)2－1＝－x2＋2x－4.故选B.‎ ‎7．y＝2x2－4x　[解析] 设这个二次函数的表达式为y＝a(x－1)2－2.‎ 根据图象过原点，得0＝a×(0－1)2－2，‎ 解得a＝2.故这个二次函数的表达式是y＝2(x－1)2－2，即y＝2x2－4x.‎ ‎8．y＝x2＋x－2　[解析] 结合表格由二次函数的对称性可知此二次函数的图象的顶点坐标是(－，－)，所以可设该二次函数的表达式为y＝a(x＋)2－，‎ 又由题表可知该二次函数的图象经过点(－1，－2)，‎ 所以－2＝a×(－1＋)2－，解得a＝1.‎ 所以该二次函数的表达式为y＝(x＋)2－＝x2＋x－2.‎ ‎9．解：由题图可知，抛物线的顶点坐标为(，4)，且经过点(0，)．‎ 设抛物线的表达式为y＝a(x－)2＋4.‎ 把点(0，)代入，可求得a＝－10.‎ 所以这支喷泉的函数表达式为 y＝－10(x－)2＋4.‎ ‎10． A ‎[解析] ∵x＝1时，ax2＝1，∴a＝1.‎ 将(－1，8)，(0，3)分别代入y＝x2＋bx＋c中，得 解得 ‎∴y与x之间的函数表达式是y＝x2－4x＋3.故选A.‎ ‎11．解：(1)因为抛物线y＝ax2＋2x＋c经过点A(0，3)，B(－1，0)，‎ 所以 解得 所以抛物线的函数表达式为y＝－x2＋2x＋3.‎ 6‎ ‎(2)抛物线y＝－x2＋2x＋3＝－(x－1)2＋4的顶点坐标为(1，4)，‎ 所以BD＝＝＝2 .‎ ‎12．解：当x＝0时，y＝2，所以点B的坐标是(0，2)．‎ 当y＝0时，x＝－2，所以点A的坐标是(－2，0)，‎ ‎∴OA＝OB，‎ ‎∴∠OAB＝45°.‎ ‎∵∠ABC＝90°，‎ ‎∴OC＝OB＝OA＝2，‎ ‎∴点C的坐标是(2，0)．‎ 设抛物线的表达式为y＝a(x－2)2，∵抛物线过点B(0，2)，∴4a＝2，解得a＝.‎ 因此抛物线的表达式为y＝(x－2)2＝x2－2x＋2.‎ ‎13．解：(1)设y＝a(x＋1)(x－6)(a≠0)，‎ 把B(5，－6)代入，得a×(5＋1)×(5－6)＝－6，‎ 解得a＝1，‎ ‎∴y＝(x＋1)(x－6)＝x2－5x－6.‎ ‎∴抛物线的表达式为y＝x2－5x－6.‎ ‎(2)存在．‎ 分别过点P，B向x轴作垂线PM和BN，垂足分别为M，N.‎ 设P(m，m2－5m－6)，四边形PACB的面积为S，‎ 则PM＝－m2＋5m＋6，AM＝m＋1，MN＝5－m，CN＝6－5＝1，BN＝6，‎ ‎∴S＝S△AMP＋S梯形PMNB＋S△BNC ‎＝(－m2＋5m＋6)(m＋1)＋(6－m2＋5m＋6)(5－m)＋×1×6‎ ‎＝－3m2＋12m＋36‎ ‎＝－3(m－2)2＋48.‎ 当m＝2时，S有最大值为48，这时m2－5m－6＝22－5×2－6＝－12，‎ ‎∴P(2，－12)．‎ ‎14．解：(1)y＝－x2－3　y＝－x－3‎ ‎(2)由 解得 ‎∴待求抛物线与y轴的交点为N(0，1)，抛物线的顶点为M(1，－1)．‎ ‎∴设抛物线的表达式为y＝a(x－1)2－1，把N(0，1)代入，得1＝a×(0－1)2－1，解得a＝2.‎ ‎∴这条抛物线的表达式为y＝2(x－1)2－1，即y＝2x2－4x＋1.‎ 6‎