福建专版2020中考数学复习方案第三单元函数及其图象第15课时二次函数的图象与性质2课件 34页

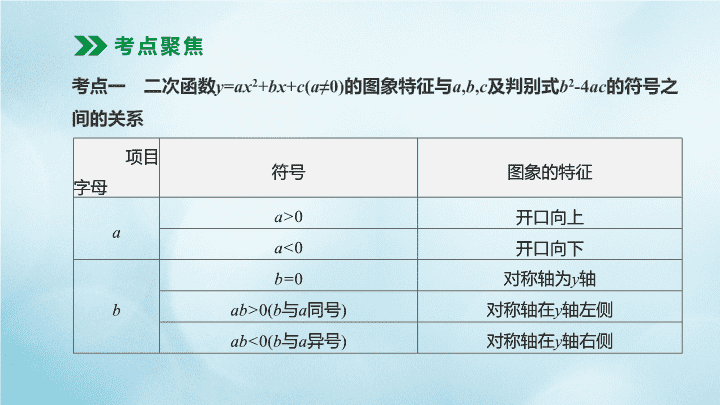
第 15 课时 二次函数的图象与性质2 第三单元　函数及其图象 考点一　二次函数y=ax2+bx+c(a≠0)的图象特征与a,b,c及判别式b2-4ac的符号之 间的关系 考点聚焦 　项目 字母　 符号 图象的特征 a a>0 开口向上 a<0 开口向下 b b=0 对称轴为y轴 ab>0(b与a同号) 对称轴在y轴左侧 ab<0(b与a异号) 对称轴在y轴右侧 　项目 字母　 符号 图象的特征 c c=0 经过原点 c>0 与y轴正半轴相交 c<0 与y轴负半轴相交 b2-4ac b2-4ac=0 　与x轴有唯一交点(顶点) b2-4ac>0 与x轴有两个不同交点 b2-4ac<0 与x轴没有交点 (续表) 【温馨提示】 当x=1时,y=a+b+c;当x=-1时,y=a-b+c. 考点二　二次函数与一元二次方程的关系 二次函数y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有着密切的关系, 二次函数的图象与x轴的交点的横坐标是对应的一元二次方程的实数根,抛物 线与x轴的交点情况可由b2-4ac的符号判定. 1.有两个交点⇔①　　　　　　⇔方程有②　 　　　 的实数根. 2.有一个交点⇔③　　　　　　⇔方程有④　　　　 的实数根. 3.没有交点⇔⑤　　　　　　⇔方程⑥　　　实数根. b2-4ac>0 两个不相等 b2-4ac=0 两个相等 b2-4ac<0 无 考点三　二次函数与不等式 二次函数与不等式的关系 (1)ax2+bx+c>0的解集 函数y=ax2+bx+c的图象位于x轴上方的部分对应的点的横坐标的取值范围. (2)ax2+bx+c<0的解集 函数y=ax2+bx+c的图象位于⑦　　　　 的部分对应的点的横坐标的取值范围. x轴下方 1.若二次函数的图象开口向下,则a　　　　0(填“=”“>”或“<”). 题组一　必会题 对点演练 < 2.已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的 一元二次方程x2-3x+m=0的两实数根是x1=　　　　,x2=　　　　. 1 2 3.[2019·泰安改编]若二次函数y=x2+bx-5 图象的对称轴为直线x=2,则关于x的方程 x2+bx-5=2x-13的解为　　　　;不等式 x2+bx-5<2x-13的解集为　　　　. [答案] x1=2,x2=4;25 [解析]抛物线的对称轴为直线x=2, 而抛物线与x轴的一个交点坐标为(5,0), 所以抛物线与x轴的另一个交点坐标 为(-1,0), 所以不等式-x2+bx+c<0的解集为x<-1 或x>5. 故答案为x<-1或x>5.图15-1 5.二次函数y=ax2+bx+c(a≠0)的图象如图15-2所示.给出下列结论:①b<0;②c>0; ③a+c0,其中正确结论的序号是　　　　. 图15-2 ②③④ 题组二　易错题 【失分点】 忽视二次函数的最大值其实已经暗示了开口方向,对a没有限制;忽略了二次函数 y=ax2+bx+c的隐含条件a≠0;混淆与坐标轴的交点和与x轴的交点的区别. [答案] C 7.已知关于x的二次函数y=(m+6)x2+2(m-1)x +m+1的图象与x轴总有交点,则m的取值范 围是　　　　. 考向一　二次函数解析式中a,b,c的意义 例1[2019·龙岩质检]如图15-3,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标 是(1,n),与y轴的交点在(0,3)和(0,6)之间(包含端点),则下列结论错误的是(　　) A.3a+b<0 B.-2≤a≤-1 C.abc>0 D.9a+3b+2c>0 图15-3 C | 考向精练 | 1.[2019·北京丰台期末]二次函数y=ax2+bx+c(a≠0)的图象如图15-4所示,那么下 列说法正确的是 (　　) A.a>0,b>0,c>0 B.a<0,b>0,c>0 C.a<0,b>0,c<0 D.a<0,b<0,c>0 图15-4 B 2.[2019·凉山州]二次函数y=ax2+ bx+c的部分图象如图15-5所示,有 以下结论:①3a-b=0;②b2- 4ac>0;③5a-2b+c>0;④4b+3c>0, 其中错误结论的个数是(　　) A.1 B.2 C.3 D.4 图15-5 [答案] A 图15-6 [答案] D 4.[2016·厦门]已知点P(m,n)在抛物线 y=ax2-x-a上,当m≥-1时,总有n≤1成立, 则a的取值范围是　　　　. 考向二　二次函数与方程、不等式的结合 例2 二次函数y=ax2+bx+c(a≠0)的图象如图15-7所示,根据图象解答下列问题: (1)写出方程ax2+bx+c=0的两个根; (2)写出不等式ax2+bx+c>0的解集; (3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围. 图15-7 解:(1)由图象可知,图象与x轴交于(1,0)和(3,0), 则方程ax2+bx+c=0的两个根为1和3. (2)由图象可知,当10. (3)由图象可知,二次函数y=ax2+bx+c(a≠0)的最大值为2,若方程ax2+bx+c=k有两个 不相等的实数根,则k必须小于y=ax2+bx+c(a≠0)的最大值,则k<2. | 考向精练 | 1.已知二次函数y=ax2+bx+c中,函数y与自变 量x的部分对应值如下表: 则当y<5时,x的取值范围是　　　　. x … -1 0 1 2 3 … y … 10 5 2 1 2 … [答案] 0n的解集是　　　　 . 图15-8 x<-3或x>1 考向三　二次函数的综合问题 例3 [2018-2019厦门九上期末]在平面直角坐标系xOy中,点A(0,2),B(p,q)在直线l 上,抛物线m经过点B,C(p+4,q),且它的顶点N在直线l上. (1)若B(-2,1), ①请在图15-9的平面直角坐标系中画出直线l与抛物线m的示意图; ②设抛物线m上的点Q的横坐标为e(-2≤e≤0),过点Q作x轴的垂线, 与直线l交于点H.若QH=d,当d随e的增大而增大时,求e的取值范围; (2)抛物线m与y轴交于点F,当抛物线m与x轴有唯一交点时, 判断△NOF的形状并说明理由. 图15-9 例3 [2018-2019厦门九上期末]在平面直角坐标系xOy中,点A(0,2),B(p,q)在直线l 上,抛物线m经过点B,C(p+4,q),且它的顶点N在直线l上. (1)若B(-2,1), ②设抛物线m上的点Q的横坐标为e(-2≤e≤0),过点Q作x轴的垂线, 与直线l交于点H.若QH=d,当d随e的增大而增大时,求e的取值范围; 图15-9 例3 [2018-2019厦门九上期末]在平面直角坐标系xOy中,点A(0,2),B(p,q)在直线l 上,抛物线m经过点B,C(p+4,q),且它的顶点N在直线l上. (2)抛物线m与y轴交于点F,当抛物线m与x轴有唯一交点时, 判断△NOF的形状并说明理由. 图15-9 | 考向精练 | 图15-10 图15-10