九年级下册数学教案 3-2 圆的对称性1 北师大版 3页

‎3.2 圆的对称性 ‎1．理解圆的旋转不变性；(重点)[来源:学#科#网]‎ ‎2．掌握圆心角、弧、弦之间相等关系的定理；(重点)‎ ‎3．能应用圆心角、弧、弦之间的关系解决问题．(难点)‎ ‎　　　　　　　　　　　　　　　　　　　‎ 一、情境导入 我们知道圆是一个旋转对称图形，无论绕圆心旋转多少度，它都能与自身重合，对称中心即为其圆心．将图中的扇形AOB(阴影部分)绕点O逆时针旋转某个角度，画出旋转之后的图形，比较前后两个图形，你能发现什么？‎ 二、合作探究 探究点：圆心角、弧、弦之间的关系 ‎【类型一】 利用圆心角、弧、弦之间的关系证明线段相等 ‎ 如图，M为⊙O上一点，＝，MD⊥OA于D，ME⊥OB于E，求证：MD＝ME.‎ 解析：连接MO，根据等弧对等圆心角，则∠MOD＝∠MOE，再由角平分线的性质，得出MD＝ME.‎ 证明：连接MO，∵ ＝，∴∠MOD＝∠MOE，又∵MD⊥OA于D，ME⊥OB于E，∴MD＝ME.‎ 方法总结：圆心角、弧、弦之间相等关系的定理可以用来证明线段相等．本题考查了等弧对等圆心角，以及角平分线的性质．[来源:Z§xx§k.Com]‎ 变式训练：见《学练优》本课时练习“课堂达标训练”第7题 ‎【类型二】 利用圆心角、弧、弦之间的关系证明弧相等 ‎ 如图，在⊙O中，AB、CD是直径，CE∥AB且交圆于E，求证：＝.‎ 解析：首先连接OE，由CE∥AB，可证得∠DOB＝∠C，∠BOE＝∠E，然后由OC＝OE，可得∠C＝∠E，继而证得∠DOB＝∠BOE，则可证得＝.‎ 证明：连接OE，∵CE∥AB，∴∠DOB＝∠C，∠BOE＝∠E.∵OC＝OE，∴∠C＝∠E，∴∠DOB＝∠BOE，∴＝.‎ 方法总结：此类题主要运用了圆心角与弧的关系以及平行线的性质．注意掌握辅助线的作法及数形结合思想的应用．‎ 变式训练：见《学练优》本课时练习“课后巩固提升”第8题 ‎【类型三】 综合运用圆心角、弧、弦之间的关系进行计算 ‎ 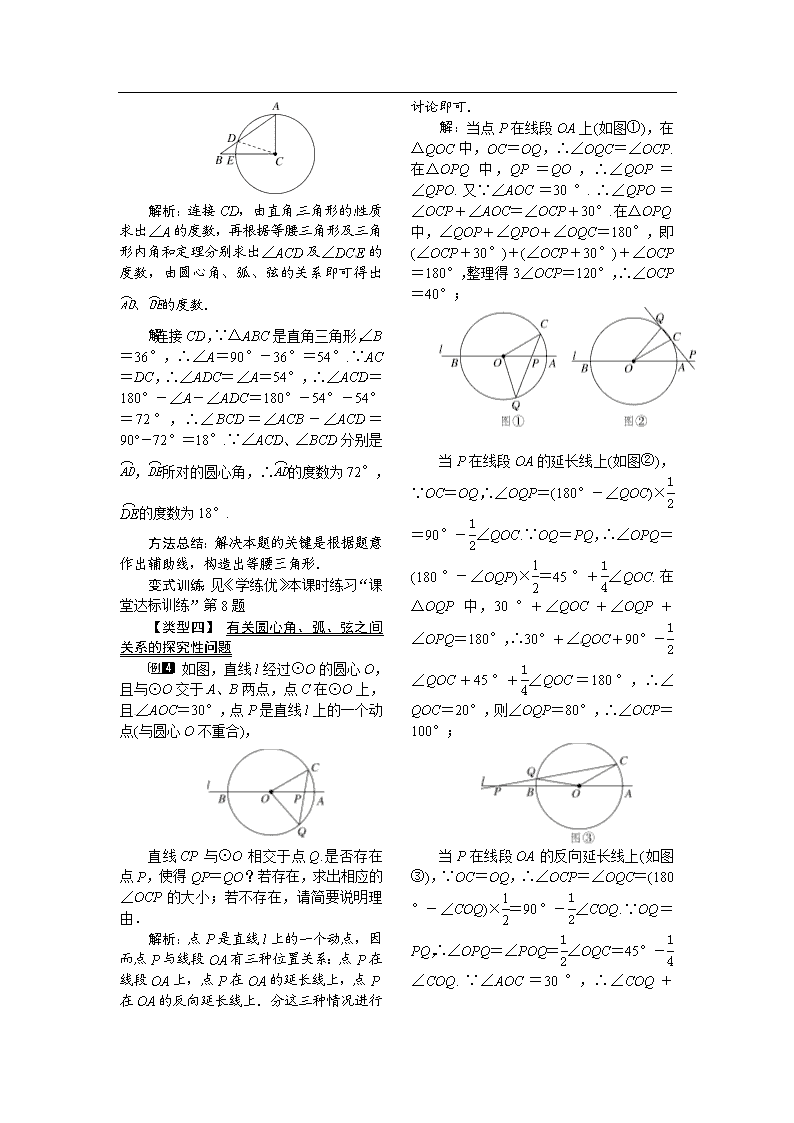如图，在△ABC中，∠ACB＝90°，∠B＝36°，以C为圆心，CA为半径的圆交AB于点D，交BC于点E.求 、的度数．‎ 解析：连接CD，由直角三角形的性质求出∠A的度数，再根据等腰三角形及三角形内角和定理分别求出∠ACD及∠DCE的度数，由圆心角、弧、弦的关系即可得出、的度数．‎ 解：连接CD，∵△ABC是直角三角形，∠B＝36°，∴∠A＝90°－36°＝54°.∵AC＝DC，∴∠ADC＝∠A＝54°，∴∠ACD＝180°－∠A－∠ADC＝180°－54°－54°＝72°，∴∠BCD＝∠ACB－∠ACD＝90°－72°＝18°.∵∠ACD、∠BCD分别是，所对的圆心角，∴的度数为72°，的度数为18°.‎ 方法总结：解决本题的关键是根据题意作出辅助线，构造出等腰三角形．‎ 变式训练：见《学练优》本课时练习“课堂达标训练”第8题 ‎【类型四】 有关圆心角、弧、弦之间关系的探究性问题 ‎ 如图，直线l经过⊙O的圆心O，且与⊙O交于A、B两点，点C在⊙O上，且∠AOC＝30°，点P是直线l上的一个动点(与圆心O不重合)，‎ 直线CP与⊙O相交于点Q.是否存在点P，使得QP＝QO？若存在，求出相应的∠OCP的大小；若不存在，请简要说明理由．‎ 解析：点P是直线l上的一个动点，因而点P与线段OA有三种位置关系：点P在线段OA上，点P在OA的延长线上，点P在OA的反向延长线上．分这三种情况进行讨论即可．‎ 解：当点P在线段OA上(如图①)，在△QOC中，OC＝OQ，∴∠OQC＝∠OCP.在△OPQ中，QP＝QO，∴∠QOP＝∠QPO.又∵∠AOC＝30°.∴∠QPO＝∠OCP＋∠AOC＝∠OCP＋30°.在△OPQ中，∠QOP＋∠QPO＋∠OQC＝180°，即(∠OCP＋30°)＋(∠OCP＋30°)＋∠OCP＝180°，整理得3∠OCP＝120°，∴∠OCP＝40°；‎ ‎[来源:学科网ZXXK]‎ 当P在线段OA的延长线上(如图②)，∵OC＝OQ，∴∠OQP＝(180°－∠QOC)×＝90°－∠QOC.∵OQ＝PQ，∴∠OPQ＝(180°－∠OQP)×＝45°＋∠QOC.在△OQP中，30°＋∠QOC＋∠OQP＋∠OPQ＝180°，∴30°＋∠QOC＋90°－∠QOC＋45°＋∠QOC＝180°，∴∠QOC＝20°，则∠OQP＝80°，∴∠OCP＝100°；‎ 当P在线段OA的反向延长线上(如图③)，∵OC＝OQ，∴∠OCP＝∠OQC＝(180°－∠COQ)×＝90°－∠COQ.∵OQ＝PQ，∴∠OPQ＝∠POQ＝∠OQC＝45°－∠COQ.∵∠AOC＝30°，∴∠COQ＋∠POQ ‎＝150°，∴∠COQ＋45°－∠COQ＝150°，∴∠COQ＝140°，∴∠OCP＝(180°－140°)×＝20°.‎ 方法总结：本题通过同圆的半径相等，将圆的问题转化为等腰三角形的问题，是一种常见的解题方法，还要注意分类讨论思想的运用．[来源:学,科,网Z,X,X,K]‎ 三、板书设计[来源:学_科_网Z_X_X_K]‎ 圆的对称性 ‎1．圆心角、弧、弦之间的关系 ‎2．应用圆心角、弧、弦之间的关系解决问题 本节课的教学策略是通过学生自己动手画图叠合、观察思考等操作活动，让学生亲身经历知识的发生、发展及其探求过程，再通过教师演示动态教具引导，让学生感受圆的旋转不变性，并得出圆心角、弧、弦三者之间的关系，能用这一关系定理，解决圆的计算证明问题，同时注重培养学生的探索能力和逻辑推理能力，力求体验数学的生活性、趣味性.‎