2019年四川省泸州市中考真题数学试题（解析版）0 14页

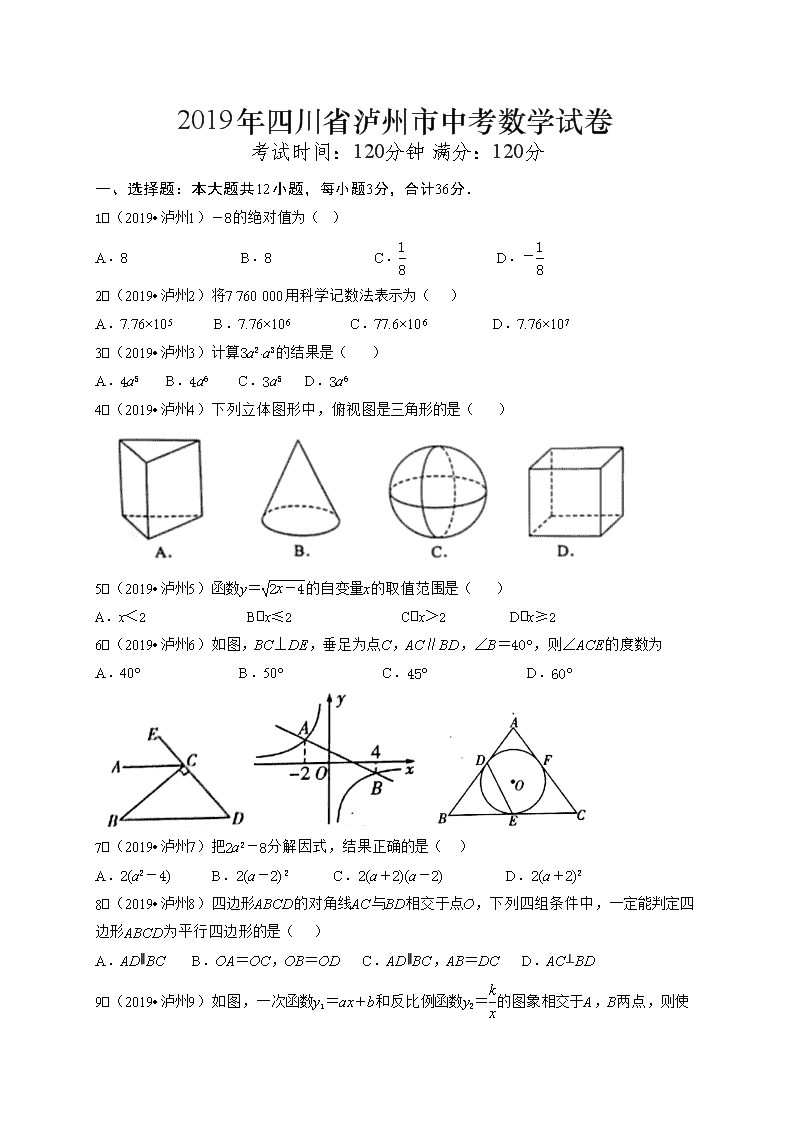
‎2019年四川省泸州市中考数学试卷 考试时间：120分钟 满分：120分 一、选择题：本大题共12小题，每小题3分，合计36分． ‎ ‎1．（2019•泸州1）－8的绝对值为（ ）‎ A．8 B．8 C． D．－ ‎2．（2019•泸州2）将7 760 000用科学记数法表示为（ ）‎ A．7.76×105 B．7.76×106 C．77.6×106 D．7.76×107‎ ‎3．（2019•泸州3）计算3a2×a3的结果是（ ）‎ A．4a5 B．4a6 C．3a5 D．3a6 ‎ ‎4．（2019•泸州4）下列立体图形中，俯视图是三角形的是（ ）‎ ‎5．（2019•泸州5）函数y＝的自变量x的取值范围是（ ）‎ A．x＜2 B．x≤2 C．x＞2 D．x≥2‎ ‎6．（2019•泸州6）如图，BC⊥DE，垂足为点C，AC∥BD，∠B＝40°，则∠ACE的度数为 A．40° B．50° C．45° D．60°‎ ‎7．（2019•泸州7）把2a2－8分解因式，结果正确的是（ ）‎ A．2(a2－4) B．2(a－2) 2 C．2(a＋2)(a－2) D．2(a＋2)2‎ ‎8．（2019•泸州8）四边形ABCD的对角线AC与BD相交于点O，下列四组条件中，一定能判定四边形ABCD为平行四边形的是（ ）‎ A．AD∥BC B．OA＝OC，OB＝OD C．AD∥BC，AB＝DC D．AC⊥BD ‎9．（2019•泸州9）如图，一次函数y1＝ax＋b和反比例函数y2＝的图象相交于A，B两点，则使y ‎1＞y2成立的x取值范围是（ ）‎ A．－2＜x＜0或0＜x＜4 B．x＜－2或0＜x＜4 C．x＜－2或x＞4 D．－2＜x＜0或x＞4‎ ‎10．（2019•泸州10）一个菱形的边长为6，面积为28，则该菱形的两条对角线的长度之和为 A．8 B．12 C．16 D．32‎ ‎11．（2019•泸州11）如图，等腰△ABC的内切圆⊙O与AB，BC，CA分别相切于点D，E，F，且AB＝AC＝5，BC＝6，则DE的长是（ ）‎ A． B． C． D． ‎12．（2019•泸州12）已知二次函数y＝(x－a－1)(x－a＋1)－3a＋7（其中x是自变量）的图象与x轴没有公共点，且当x＜－1时，y随x的增大而减小，则实数a的取值范围是（ ）‎ A．a＜2 B．a＞－1 C．－1＜a≤2 D．－1≤a＜2‎ 二、填空题：本大题共4小题，每小题3分，合计12分．‎ ‎13．（2019•泸州13）4的算术平方根是 .‎ ‎14．（2019•泸州14）在平面直角坐标系中，点M（a，b）与点N（3，－1）关于x轴对称，则a＋b的值是 . 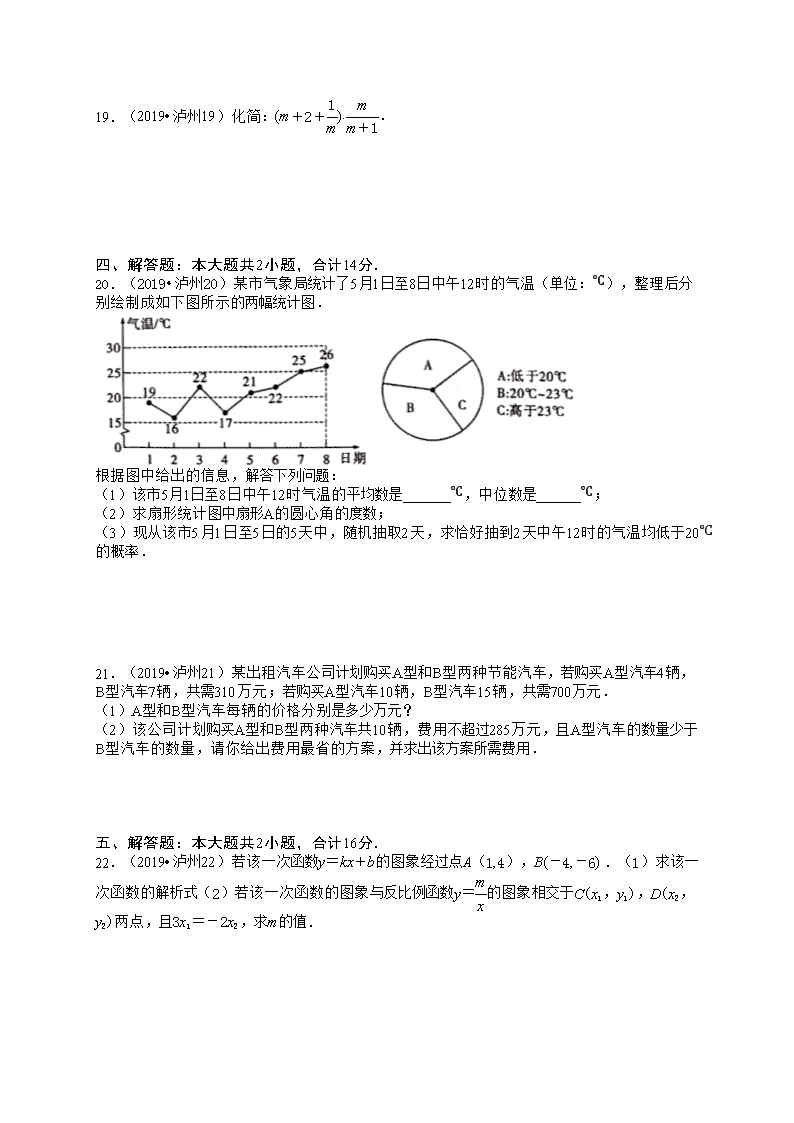‎ ‎15．（2019•泸州15）已知x1，x2是一元二次方程x2－x－4＝0的两实数根，则(x1＋4)(x2＋4)的值是 .‎ ‎16．（2019•泸州16）如图，在等腰R△ABC中，∠C＝90°，AC＝15，点E在边CB上，CE＝2EB，点D在边AB上，CD⊥AE，垂足为F，则AD的长为 ． ‎ 三、解答题：本大题共3小题，合计18分．‎ ‎17．（2019•泸州17）计算：(π＋1)0＋(－2)2－×sin30°.‎ ‎18．（2019•泸州18）如图，AB∥CD，AD和BC相交于点O，OA＝OD．求证：OB＝OC．‎ ‎19．（2019•泸州19）化简：(m＋2＋)×．‎ 四、解答题：本大题共2小题，合计14分．‎ ‎20．（2019•泸州20）某市气象局统计了5月1日至8日中午12时的气温（单位：℃），整理后分别绘制成如下图所示的两幅统计图．‎ 根据图中给出的信息，解答下列问题：‎ ‎（1）该市5月1日至8日中午12时气温的平均数是 ℃，中位数是 ℃；‎ ‎（2）求扇形统计图中扇形A的圆心角的度数；‎ ‎（3）现从该市5月1日至5日的5天中，随机抽取2天，求恰好抽到2天中午12时的气温均低于20℃的概率．‎ ‎21．（2019•泸州21）某出租汽车公司计划购买A型和B型两种节能汽车，若购买A型汽车4辆，B型汽车7辆，共需310万元；若购买A型汽车10辆，B型汽车15辆，共需700万元．‎ ‎（1）A型和B型汽车每辆的价格分别是多少万元？‎ ‎（2）该公司计划购买A型和B型两种汽车共10辆，费用不超过285万元，且A型汽车的数量少于B型汽车的数量，请你给出费用最省的方案，并求出该方案所需费用．‎ 五、解答题：本大题共2小题，合计16分．‎ ‎22．（2019•泸州22）若该一次函数y＝kx＋b的图象经过点A（1,4），B(－4,－6) ．（1）求该一次函数的解析式（2）若该一次函数的图象与反比例函数y＝的图象相交于C(x1，y1)，D(x2，y2)两点，且3x1＝－2x2，求m的值．‎ ‎23．（2019•泸州23）如图，海中有两个小岛C，D，某渔船在海中的A处测得小岛D位于东北方向上，且相距20n mile，该渔船自西向东航行一段时间后到达点B处，此时测得小岛C恰好在点B的正北方向上，且相距50n mile，又测得点B与小岛D相距20n mile．‎ ‎（1）求sin∠ABD的值；（2）求小岛C，D之间的距离（计算过程中的数据不取近似值）．‎ 五、解答题：本大题共2小题，合计24分．‎ ‎24．（2019•泸州24）如图，AB为⊙O的直径，点P在AB的延长线上，点C在⊙O上，且PC2＝PB×PA．（1）求证：PC是⊙O的切线；（2）已知PC＝20，PB＝10，点D是的中点，DE⊥AC，垂足为E，DE交AB于点F，求EF的长．‎ ‎25．（2019•泸州25）如图，在平面直角坐标系xOy中，已知二次函数y＝ax2＋bx＋c的图象经过点A(－2，0)，C(0，－6)，其对称轴为直线x＝2．‎ ‎（1）求该二次函数的解析式；‎ ‎（2）若直线y＝－x＋m将△AOC的面积分成相等的两部分，求m的值；‎ ‎（3）点B是该二次函数图象与轴的另一个交点，点D是直线上位于轴下方的动点，点E是第四象限内该二次函数图象上的动点，且位于直线x＝2的右侧．若以点E为直角顶点的△BED与△AOC相似，求点E的坐标．‎ ‎2019年四川省泸州市中考数学试卷 考试时间：120分钟 满分：120分 一、选择题：本大题共12小题，每小题3分，合计36分． ‎ ‎1．（2019•泸州1）－8的绝对值为（ ）‎ A．8 B．8 C． D．－ ‎{答案}A ‎{解析}本题考查了绝对值的意义，根据负数的绝对值等于它的相反数，得|－8|＝8．因此本题选A．‎ ‎2．（2019•泸州2）将7 760 000用科学记数法表示为（ ）‎ A．7.76×105 B．7.76×106 C．77.6×106 D．7.76×107‎ ‎{答案} B ‎{解析}本题考查了科学记数法的表示方法，126000000=1.26×100000000=1.26×108，因此本题选B．‎ ‎3．（2019•泸州3）计算3a2×a3的结果是（ ）‎ A．4a5 B．4a6 C．3a5 D．3a6 ‎ ‎{答案}C ‎{解析}本题考查了单项式与单项式相乘，3a2•a3＝(3×1)(a2•a3)＝3a5，因此本题选C．‎ ‎4．（2019•泸州4）下列立体图形中，俯视图是三角形的是（ ）‎ ‎{答案}A ‎{解析}本题考查了简单几何体的三视图，从上面看得到的视图是俯视图．从上面看只有三棱柱的得到的图形是三角形，因此本题选A．‎ ‎5．（2019•泸州5）函数y＝的自变量x的取值范围是（ ）‎ A．x＜2 B．x≤2 C．x＞2 D．x≥2‎ ‎{答案} D ‎{解析}本题考查了函数自变量的取值范围，本质是二次根式有意义的条件．由题意，得2x－4≥0，解得x≥2，因此本题选D．‎ ‎6．（2019•泸州6）如图，BC⊥DE，垂足为点C，AC∥BD，∠B＝40°，则∠ACE的度数为（ ）‎ A．40° B．50° C．45° D．60°‎ ‎{答案}B ‎{解析}本题考查了平行线的性质和直角三角形两锐角互余的性质．先由BC⊥DE，得到∠B＋∠D＝90°，从而∠D＝90°－40°＝50°；再由AC∥BD，得到∠ACE＝∠D＝50°；因此本题选B．‎ ‎7．（2019•泸州7）把2a2－8分解因式，结果正确的是（ ）‎ A．2(a2－4) B．2(a－2) 2 C．2(a＋2)(a－2) D．2(a＋2)2‎ ‎{答案}C ‎{解析}本题考查了提取公因式法以及运用公式法分解因式，2a2－8＝2(a2－4)＝2(a＋2)(a－2)，因此本题选C．‎ ‎8．（2019•泸州8）四边形ABCD的对角线AC与BD相交于点O，下列四组条件中，一定能判定四边形ABCD为平行四边形的是（ ）‎ A．AD∥BC B．OA＝OC，OB＝OD C．AD∥BC，AB＝DC D．AC⊥BD ‎{答案}B ‎{解析}本题考查了平行四边形的判定，关键是熟练掌握平行四边形的判定定理．根据对角线互相平分的四边形是平行四边形，因此本题选B．‎ ‎9．（2019•泸州9）如图，一次函数y1＝ax＋b和反比例函数y2＝的图象相交于A，B两点，则使y1＞y2成立的x取值范围是（ ）‎ A．－2＜x＜0或0＜x＜4 B．x＜－2或0＜x＜4‎ C．x＜－2或x＞4 D．－2＜x＜0或x＞4‎ ‎{答案} B ‎{解析}本题考查了反比例函数的图象性质和一次函数的图象性质，由一次函数与反比例函数的图象相交于A、B两点，图中使一次函数的值大于反比例函数的值的x的取值范围是x＜－2或0＜x＜4，因此本题选B．‎ ‎10．（2019•泸州10）一个菱形的边长为6，面积为28，则该菱形的两条对角线的长度之和为（ ）‎ A．8 B．12 C．16 D．32‎ ‎{答案} C ‎{解析}本题考查了菱形的性质及勾股定理，根据菱形对角线互相垂直平分，设菱形两对角线的长为2a、2b，则×2a×2b＝28，a2＋b2＝62，即ab＝14，a2＋b2＝36，∴(a＋b)2＝ a2＋b2＋2ab＝36＋2×14＝64，∴a＋b＝8，∴2a＋2b＝16，因此本题选C．‎ ‎11．（2019•泸州11）如图，等腰△ABC的内切圆⊙O与AB，BC，CA分别相切于点D，E，F，且AB＝AC＝5，BC＝6，则DE的长是（ ）‎ A． B． C． D． ‎{答案} D ‎{解析}本题考查了三角形内切圆半径的求法及切线长的性质，如图，连接OA、OE、OB，OB交DE于点H，显然点A、O、E在一条直线上，AE垂直平分BC，则BE＝BC＝×6＝3，由勾股定理得，AE＝＝4，设⊙O的半径为r，则S△ABC＝ (AB＋AC＋BC)×r，∴×6×4＝ (5＋5＋6)×r，解得r＝；由勾股定理得，OB＝＝＝，由切线长的性质知BD＝BE，OB⊥DE，再在△OBE中，由×OB×EH＝×BE×OE，得EH＝＝，∴DE＝2EH＝，因此本题选D．‎ H ‎12．（2019•泸州12）已知二次函数y＝(x－a－1)(x－a＋1)－3a＋7（其中x是自变量）的图象与x轴没有公共点，且当x＜－1时，y随x的增大而减小，则实数a的取值范围是（ ）‎ A．a＜2 B．a＞－1 C．－1＜a≤2 D．－1≤a＜2‎ ‎{答案} D ‎{解析}本题考查了二次函数的图象与性质，根据函数关系式知抛物线的对称轴为x＝a，而抛物线开口向上，由x＜－1时，y随x的增大而减小可知a≥－1；又抛物线与x轴没有公共点，∴当x＝a时，y＝－1－3a＋7＞0，∴a＜2，∴－1≤a＜2，因此本题选D．‎ ‎{题型:2-填空题}二、填空题：本大题共4小题，每小题3分，合计12分．‎ ‎13．（2019•泸州13）4的算术平方根是 .‎ ‎{答案}2‎ ‎{解析}本题考查了算术平方根的求法，∵22=4，∴4的算术平方根2．‎ ‎14．（2019•泸州14）在平面直角坐标系中，点M（a，b）与点N（3，－1）关于x轴对称，则a＋b的值是 . ‎ ‎{答案}4.‎ ‎{解析}本题考查了关于x轴对称点的坐标的坐标特点：横坐标不变，纵坐标互为相反数可得a＝3，b＝1，然后算出a＋b＝4．‎ ‎15．（2019•泸州15）已知x1，x2是一元二次方程x2－x－4＝0的两实数根，则(x1＋4)(x2＋4)的值是 .‎ ‎{答案}16‎ ‎{解析}本题考查了一元二次方程根与系数的关系，由题意，得x1＋x2＝1，x1x2＝－4，∴(x1＋4)(x2＋4)＝x1x2＋4(x1＋x2)＋16＝－4＋4×1＋16＝16．‎ ‎16．（2019•泸州16）如图，在等腰R△ABC中，∠C＝90°，AC＝15，点E在边CB上，CE＝2EB，点D在边AB上，CD⊥AE，垂足为F，则AD的长为 ． ‎ ‎{答案}9．‎ ‎{解析}本题考查了平行线分线段成比例、相似三角形的判定与性质，过点E作EG∥CD交AB于点G，则＝＝2，又由∠ACE＝90°，CF⊥AE可得△ACF∽△AEC，可得AC2＝AF×AE，同理CE2＝EF×AE，∴＝ ＝＝()2＝，即AD:DG:GB＝9:4:2，AD＝AB＝×15＝9．‎ G ‎{题型:4-解答题}三、解答题：本大题共3小题，合计18分．‎ ‎17．（2019•泸州17）计算：(π＋1)0＋(－2)2－×sin30°.‎ ‎{解析}本题考查了实数的运算，根据实数运算法则直接解答．‎ ‎{答案}解：原式＝1＋4－2×＝4.‎ ‎18．（2019•泸州18）如图，AB∥CD，AD和BC相交于点O，OA＝OD．求证：OB＝OC．‎ ‎{解析}本题考查了平行线的性质和全等三角形的性质和判定，由AB∥CD得到∠B＝∠C，根据AAS证△AOB≌△DOC，根据全等三角形的性质推出即可，也可用ASA证明三角形全等．‎ ‎{答案}证明：∵AD与BC相交于点O，∴∠AOB＝∠DOC，‎ ‎∵AB∥CD，∴∠B＝∠C，‎ 在△AOB和△DOC中， ‎∴△AOB≌△DOC中（AAS），∴OB＝OC．‎ ‎19．（2019•泸州19）化简：(m＋2＋)×．‎ ‎{解析}本题考查了分式的混合运算，先把括号式子通分，然后进行乘法运算，最后注意约分化简．‎ ‎{答案}解：原式＝ ×＝×＝m＋1．‎ ‎{题型:4-解答题}四、解答题：本大题共2小题，合计14分．‎ ‎20．（2019•泸州20）某市气象局统计了5月1日至8日中午12时的气温（单位：℃），整理后分别绘制成如下图所示的两幅统计图．‎ 根据图中给出的信息，解答下列问题：‎ ‎（1）该市5月1日至8日中午12时气温的平均数是 ℃，中位数是 ℃；‎ ‎（2）求扇形统计图中扇形A的圆心角的度数；‎ ‎（3）现从该市5月1日至5日的5天中，随机抽取2天，求恰好抽到2天中午12时的气温均低于20℃的概率．‎ ‎{解析}本题考查了统计和概率的相关知识，（1）从折线统计图中，求出气温的平均数为(19+16+22+17+21+22+25+26)÷8=21（℃），中位数为(21+22)÷2=21.5；（2）扇形A的圆心角的度数等于×360°即可得到结果；（3）列举出所有等可能的情况数，找出恰好抽到2天中午12时的气温均低于20℃的的情况数，即可求出所求的概率．．‎ ‎{答案}解：（1）21℃，中位数是21.5℃；‎ ‎（2）因为低于20℃的天数有3天，‎ 所以扇形统计图中扇形A的圆心角的度数为：360°×=135°；‎ 答：扇形统计图中扇形A的圆心角的度数是135°．‎ ‎（3）设这个月1日至5日5天中午12时的气温依次记为A1，A2，A3，A4，A5，随机抽取2天中午12时的气温，共有：（A1，A2），（A1，A3），（A1，A4），（A1，A5），（A2，A3），（A2，A4），（A2，A5），（A3，A4），（A3，A5），（A4，A5）10种不同的取法．‎ 其中中午12时气温低于20℃的为A1，A2，A4，而恰好有2天中午12时气温均低于20℃的情况有（A1，A2），（A1，A4），（A2，A4）3种不同的取法，‎ 因此恰好抽到2天中午12时气温均低于20℃的概率为．‎ ‎21．（2019•泸州21）某出租汽车公司计划购买A型和B型两种节能汽车，若购买A型汽车4辆，B型汽车7辆，共需310万元；若购买A型汽车10辆，B型汽车15辆，共需700万元．‎ ‎（1）A型和B型汽车每辆的价格分别是多少万元？‎ ‎（2）该公司计划购买A型和B型两种汽车共10辆，费用不超过285万元，且A型汽车的数量少于B型汽车的数量，请你给出费用最省的方案，并求出该方案所需费用．‎ ‎{解析}本题考查了二元一次方程组和一元一次不等式组的应用，注意理解题意，找出题目蕴含的数量关系，列出方程组或不等式组解决问题．‎ ‎（1）设A型汽车每辆的价格为x万元，B型汽车每辆的价格为y万元，根据“A型汽车4辆，B型汽车7辆，共需310万元；A型汽车10辆，B型汽车15辆，共需700万元”列出方程组解决问题；‎ ‎（2）设购买A型汽车m辆，则购买B型汽车(10－m)辆，由“购买A型和B型两种汽车共10辆，费用不超过285万元”和“A型汽车的数量少于B型汽车的数量”列出不等式组探讨得出答案即可．‎ ‎{答案}解：（1）设A型汽车每辆的价格为x万元，B型汽车每辆的价格为y万元，由题意得：‎ 解得 答：A型汽车每辆的价格为25万元，B型汽车每辆的价格为30万元． ‎ ‎（2）设购买A型汽车m辆，则购买B型汽车(10-m)辆，由题意得：‎ 解得：3≤m＜5．‎ 因为m是整数，所以m＝3或4．‎ 当m＝3时，该方案所需费用为：25×3＋30×7＝285万元；‎ 当m＝4时，该方案所需费用为：25×4＋30×6＝280万元．‎ 答：费用最省的方案是购买A型汽车4辆，则购买B型汽车6辆，该方案所需费用为280万元．‎ ‎{题型:4-解答题}五、解答题：本大题共2小题，合计16分．‎ ‎22．（2019•泸州22）若该一次函数y＝kx＋b的图象经过点A（1,4），B(－4,－6) ．‎ ‎（1）求该一次函数的解析式；‎ ‎（2）若该一次函数的图象与反比例函数y＝的图象相交于C(x1，y1)，D(x2，y2)两点，且3x1＝－2x2，求m的值．‎ ‎{解析}本题考查了一次函数与反比例函数的综合运用，（1）用待定系数法求一次函数关系式，直接代入即可；（2）联立一次函数与反比例函数关系式，转化为一元二次方程，用根与系数的关系，转化为解二元一次方程组解题．‎ ‎{答案}解：（1）由题意，得：‎ ‎ 解得 所以一次函数解析式为y＝2x＋2；‎ ‎（2）联立消去y得：‎ ‎2x2＋2x－m＝0，‎ 则x1＋x2＝－1，因为3x1＝－2x2，‎ 解得： 所以点C(2.6)．‎ 因为反比例函数y＝的图象过点C(2,6)，‎ 所以m＝12．‎ ‎23．（2019•泸州23）如图，海中有两个小岛C，D，某渔船在海中的A处测得小岛D位于东北方向上，且相距20n mile，该渔船自西向东航行一段时间后到达点B处，此时测得小岛C恰好在点B的正北方向上，且相距50n mile，又测得点B与小岛D相距20n mile．‎ ‎（1）求sin∠ABD的值；‎ ‎（2）求小岛C，D之间的距离（计算过程中的数据不取近似值）．‎ ‎{解析}本题是解直角三角形的应用——方向角问题，关键是将解斜三角形问题转化为解直角三角形问题．‎ ‎{答案}解：（1）如图，过点D作DE⊥AB，垂足为E，‎ 在R△AED中，AD＝20，∠DAE＝45°，‎ 所以DE＝20×sin45°＝20，‎ 在R△BED中，BD＝20，‎ 所以sin∠ABD＝＝＝；‎ ‎（2）过点D作DF⊥BC，垂足为F，‎ 在R△BED中，DE＝20，BD＝20，‎ 所以BE＝＝＝40，‎ 因为四边形BFDE是矩形，所以DF＝EB＝40，BF＝DE＝20，‎ 所以CF＝BC－BF＝30．‎ 在R△CDF中，CD＝＝＝50．‎ 因此小岛C，D之间相距50 n mile．‎ ‎{题型:4-解答题}五、解答题：本大题共2小题，合计24分．‎ ‎24．（2019•泸州24）如图，AB为⊙O的直径，点P在AB的延长线上，点C在⊙O上，且PC2＝PB×PA．‎ ‎（1）求证：PC是⊙O的切线；‎ ‎（2）已知PC＝20，PB＝10，点D是的中点，DE⊥AC，垂足为E，DE交AB于点F，求EF的长．‎ ‎{解析}本题考查了圆的切线的判定和圆中有关的计算问题，（1）连接OC，由△PBC∽△PCA得出∠PCB＝∠PAC，再利用直径所对的圆周角是直角证明OC⊥PC即可；（2）连接OD，先求出AB的长，再根据△PBC∽△PCA，结合勾股定理求出BC，进而利用△DOF∽△ACB，求出AF的长，进一步求EF的长．‎ ‎{答案}（1）证明：连接OC，因为PC2＝PB×PA，即＝，‎ ‎ 又∠P＝∠P，‎ 所以△PBC∽△PCA，‎ 所以∠PCB＝∠PAC．‎ 因为AB是⊙O的直径，‎ 所以∠ACB＝90°，‎ 所以∠A＋∠ABC＝90°，‎ 因为OC＝OB，‎ 所以∠OBC＝∠OCB，‎ 所以∠PCB＋∠OCB＝90°，即OC⊥PC，‎ 所以PC为⊙O的切线；‎ ‎（2）解：连接OD，因为PC＝20，PB＝10，PC2＝PB×PA，‎ 所以PA＝＝40，‎ 所以AB＝30，‎ 因为△PBC∽△PCA，‎ 所以＝＝2，设BC＝x，则AC＝2x，‎ 在R△ABC中，x2＋(2x)2＝302，所以x＝6，即BC＝6，‎ 因为点D为的中点，AB为⊙O的直径，所以∠AOD＝90°，‎ 所以DE⊥AC，所以∠AEF＝90°，又∠ACB＝90°，‎ 所以DE∥BC，所以∠DFO＝∠ABC，‎ 所以△DOF∽△ACB，＝＝，‎ 所以OF＝OD＝，即AF＝，‎ 因为EF∥BC，所以＝＝，‎ 所以EF＝BC＝．‎ ‎25．（2019•泸州25）如图，在平面直角坐标系xOy中，已知二次函数y＝ax2＋bx＋c的图象经过点A(－2，0)，C(0，－6)，其对称轴为直线x＝2．‎ ‎（1）求该二次函数的解析式；‎ ‎（2）若直线y＝－x＋m将△AOC的面积分成相等的两部分，求m的值；‎ ‎（3）点B是该二次函数图象与轴的另一个交点，点D是直线上位于轴下方的动点，点E是第四象限内该二次函数图象上的动点，且位于直线x＝2的右侧．若以点E为直角顶点的△BED与△AOC相似，求点E的坐标．‎ ‎{解析}本题考查了二次函数与一次函数及相似三角形的综合运用，（1）直接用待定系数法求二次函数的关系式；（2）根据题意，先求直线与AC的交点坐标，进而由面积关系列出方程解题；（3）分两种情况：△DEB∽△AOC或△BED∽△AOC，结合二次函数的性质分别列出方程即可．‎ ‎{答案}解：（1）由已知得：‎ 解得： 所以该二次函数的解析式为y＝x2－2x－6；‎ ‎（2）由已知可得，直线AC的解析式为：y＝－3x－6，‎ 联立解得：x＝－ (m＋6)，‎ 直线y＝－x＋m与y轴交于点(0，m)，‎ 因为△AOC的面积为×2×6＝6，‎ 所以由题意得：× (m＋6) (m＋6)＝3，‎ 所以m＝－2或m＝－10（舍去）,‎ 所以m＝－2；‎ ‎（3）因为OA＝2，OC＝6，所以＝3，‎ 若以点E为直角顶点的△BED与△AOC相似，则：‎ ‎△DEB∽△AOC或△BED∽△AOC．‎ ‎①当△△DEB∽△AOC时，＝＝3，‎ 过点E作EF⊥直线x＝2，垂足为f，过点B作BG⊥FE，垂足为G，‎ 写R△BEG∽R△EDF，‎ 因为＝ ＝3，所以BG＝3EF，‎ 设点E(h，k)（2＜h＜6，－8＜k＜0），‎ 则BG＝－k，EF＝h－2，‎ 所以－k＝3(h－2)，即k＝6－3h，‎ 因为点E(h，k)在该二次函数图象上，‎ 所以h2－2h－6＝6－3h，‎ 解得：h＝4或h＝－6（舍去），‎ 所以点E的坐标为(4，－6)；‎ ‎②当△BED∽△AOC时，＝＝，‎ 过点E作EM⊥直线x＝2，垂足为M，过点B作BN⊥ME，垂足为N，则R△BEN∽R△EDM，‎ 因为＝＝，所以BN＝EM，‎ 设点E(p，q)（2＜p＜6，－8＜q＜0），‎ 所以BN＝－q，EM＝p－2，‎ 所以－q＝ (p－2)，即q＝ (2－ p)，‎ 因为点E(p，q)在该二次函数图象上，‎ 所以p2－2p－6＝ (2－p)，‎ 解得：p＝或p＝（舍去），‎ 所以点E的坐标为(，)；‎ 综上知，点E的坐标为(4，－6)或(，) ．‎