2018年安徽省淮南市潘集区中考联考模拟卷 11页

‎ 2017～2018学年度潘集区九年级第二次联考数学试卷 题号 一 二 三 四 五 六 七 总分 得分 ‎[来源:学科网]‎ 一、选择题（共10小题，每小题4分，满分40分），在每小题给出的四个选项中，只有一项是符合题目的 ‎1．下列四个圆形图案中，分别以它们所在圆的圆心为旋转中心，顺时针旋转120°后，能与原图形完全重合的是（　　）‎ A． B． C． D．‎ ‎ ‎ ‎2．如图，点A，B，C是⊙O上的三点，已知∠AOB=100°，那么∠ACB的度数是（　　）‎ ‎ A．30° B．40° C．50° D．60°[来源:学§科§网Z§X§X§K]‎ ‎3．已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列结论中正确的是（　　）‎ ‎ ‎ ‎ A．ac＞0 B．当x＞1时，y随x的增大而增大 C．2a+b=1 D．方程ax2+bx+c=0有一个根是x=3‎ ‎4．2015年某县GDP总量为1000亿元，计划到2017年全县GDP总量实现1210亿元的目标．如果每年的平均增长率相同，那么该县这两年GDP总量的平均增长率为（　　）‎ A．1.21% B．8% C．10% D．12.1%‎ ‎5．已知3是关于x的方程x2﹣（m+1）x+2m=0的一个实数根，并且这个方程的两个实数根恰好是等腰△ABC的两条边的边长，则△ABC的周长为（　　）‎ A．7 B．10 C．11 D．10或11‎ ‎6．已知二次函数y=（x﹣1）2+4，若y随x的增大而减小，则x的取值范围是（　　）‎ A．x＜﹣1 B．x＞4 C．x＜1 D．x＞1‎ ‎7．二次函数y=﹣2x2+4x+1的图象如何平移可得到y=﹣2x2的图象（　　）‎ A．向左平移1个单位，向上平移3个单位 B．向右平移1个单位，向上平移3个单位 C．向左平移1个单位，向下平移3个单位 D．向右平移1个单位，向下平移3个单位 ‎8．如图，将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′，若∠AOB=15°，则∠AOB′的度数是（　　）‎ ‎ A．25° B．30° ‎ C．35° D．40°‎ ‎9．如图，将△ABC绕点P顺时针旋转90°得到△A′B′C′，则点P的坐标是（　　）‎ ‎[来源:学科网ZXXK]‎ ‎ A．（1，1） B．（1，2）‎ ‎ C．（1，3） D．（1，4）‎ ‎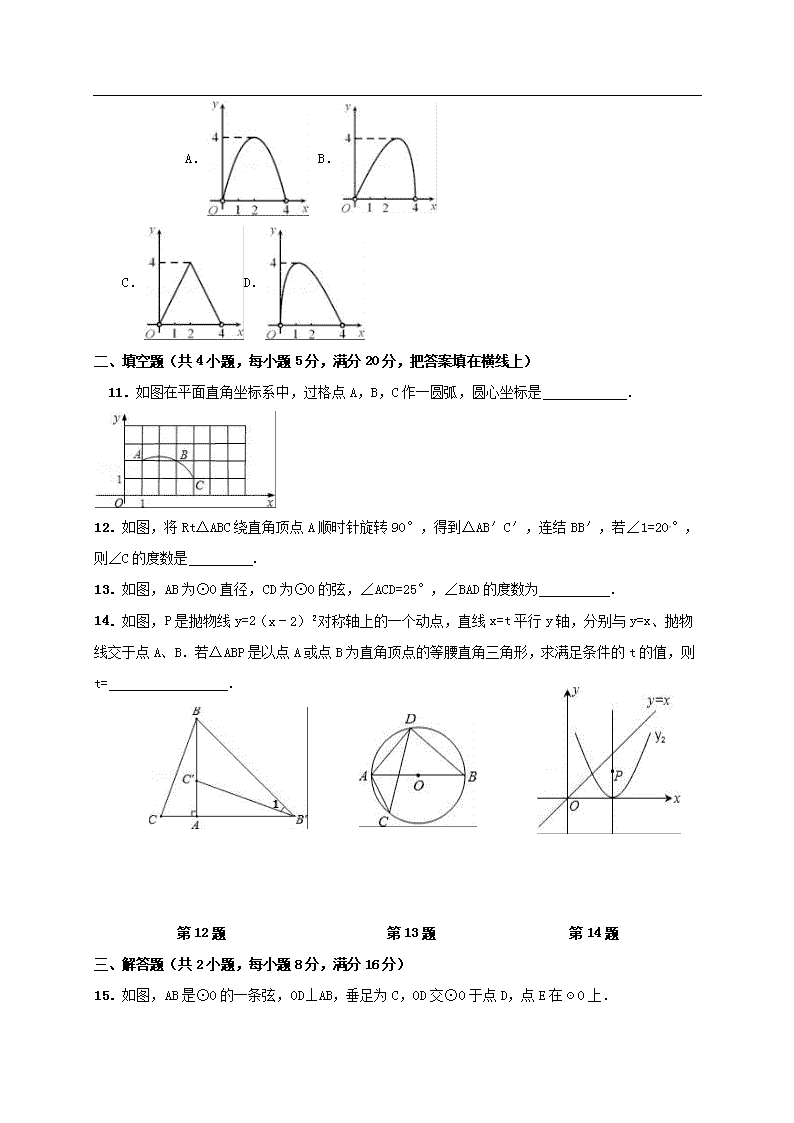10．如图，点C是以点O为圆心，AB为直径的半圆上的动点（点C不与点A，B重合），AB=4．设弦AC的长为x，△ABC的面积为y，则下列图象中，能表示y与x的函数关系的图象大致是（　　）‎ A． B． C．D．‎ 二、填空题（共4小题，每小题5分，满分20分，把答案填在横线上）‎ ‎11．如图在平面直角坐标系中，过格点A，B，C作一圆弧，圆心坐标是　 　．‎ ‎12．如图，将Rt△ABC绕直角顶点A顺时针旋转90°，得到△AB′C′，连结BB′，若∠1=20°，则∠C的度数是　 　．‎ ‎13．如图，AB为⊙O直径，CD为⊙O的弦，∠ACD=25°，∠BAD的度数为　 　．‎ ‎14．如图，P是抛物线y=2（x﹣2）2对称轴上的一个动点，直线x=t平行y轴，分别与y=x、抛物线交于点A、B．若△ABP是以点A或点B为直角顶点的等腰直角三角形，求满足条件的t的值，则t=　 　．‎ 第12题 第13题 第14题 三、解答题（共2小题，每小题8分，满分16分）‎ ‎15．如图，AB是⊙O的一条弦，OD⊥AB，垂足为C，OD交⊙O于点D，点E在☉O上．‎ ‎（1）若∠AOD=54°，求∠DEB的度数；‎ ‎（2）若OC=3，OA=5，求弦AB的长．‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎16．小李想用篱笆围成一个周长为60米的矩形场地，矩形面积S（单位：平方米）随矩形一边长x（单位：米）的变化而变化,求S与x之间的函数关系式，并写出自变量x的取值范围.‎ 四、解答题（共2小题，每小题8分，满分16分）‎ ‎17．(8分)正方形网格中(网格中的每个小正方形边长是1)，△ABC的顶点均在格点上，请在所给的直角坐标系中解答下列问题：‎ ‎(1)作出△ABC绕点A逆时针旋转90°的△AB1C1，再作出△AB1C1关于原点O成中心对称的△A1B2C2．‎ ‎(2)点B1的坐标为 ，点C2的坐标为 ．‎ A B C O x y 第17题图 ‎18．(8分)已知二次函数y＝x2－2x－3．‎ ‎(1)用配方法将表达式化为y＝(x－h)2＋k的形式；‎ ‎(2)求这个函数图象与x轴的交点坐标．‎ ‎ ‎ ‎ ‎ ‎[来源:学+科+网]‎ 五、解答题（共2小题，每小题10分，满分20分）‎ ‎19．关于x的一元二次方程x2+3x+m﹣1=0的两个实数根分别为x1，x2．‎ ‎（1）求m的取值范围；‎ ‎（2）若2（x1+x2）+x1x2+10=0，求m的值．‎ ‎20．九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：‎ 时间x（天）‎ ‎1≤x＜50‎ ‎50≤x≤90[来源:学科网ZXXK]‎ 售价（元/件）‎ x+40‎ ‎90‎ 每天销量（件）‎ ‎200﹣2x 已知该商品的进价为每件30元，设销售该商品的每天利润为y元．‎ ‎（1）求出y与x的函数关系式；‎ ‎（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？‎ 六、解答题（共2小题，每小题12分，满分24分）‎ ‎21．如图，四边形ABCD内接于⊙O，∠DAE是四边形ABCD的一个外角，且AD平分∠CAE．‎ 求证：DB=DC．‎ ‎ ‎ ‎22．如图，已知抛物线的顶点为A（1，4），抛物线与y轴交于点B（0，3），与x轴交于C、D两点．点P是x轴上的一个动点．‎ ‎（1）求此抛物线的解析式；[来源:学,科,网]‎ ‎（2）求C、D两点坐标及△BCD的面积；‎ ‎（3）若点P在x轴上方的抛物线上，满足S△PCD=S△BCD，求点P的坐标．‎ ‎ ‎ ‎　七、解答题（共1小题，满分14分）‎ ‎23.正方形ABCD中，E是CD边上一点，‎ ‎（1）将△ADE绕点A按顺时针方向旋转，使AD、AB重合，得到△ABF，如图1所示．观察可知：与DE相等的线段是　 ，∠AFB= 　 　.‎ ‎（2）如图2，正方形ABCD中，P、Q分别是BC、CD边上的点，且∠PAQ=45°，试通过旋转的方式说明：DQ+BP=PQ ‎（3）在（2）题中，连接BD分别交AP、AQ于M、N，你还能用旋转的思想说明BM2+DN2=MN2． ‎ ‎ ‎ ‎ ‎ ‎ 学校____________ 班级___________ 姓名_______________ 考号/条形码 __________________________________ 座位号_____________‎ ‎………………………………………………………………装……………………………………………订……………………………………………线…………………………………………………………………‎ 潘集区2017-2018学年度九年级第二次联考 数学试卷参考答案 一、选择题（共10小题，每小题4分，满分40分）‎ ‎1．A．2．C3．D．4． C．5． D．6． C．7．C．8． B．9． B．10．B．‎ 二、填空题（共4小题，每小题5分，满分20分）‎ ‎11．（2，0）　．12．　65°　．13．　65°　．14．t=　或1或3　．‎ 三、解答题（共2小题，每小题8分，满分16分）‎ ‎15． 解：（1）∵OD⊥AB，∴=，‎ ‎∴∠DEB=∠AOD=×54°=28°．…………………………………….4分 ‎（2）∵OC=3，OA=5， ∴AC=4，‎ ‎∵OD⊥AB， ∴弧AD=弧BD=弧AB，‎ ‎∴AC=BC=AB=4， ∴AB=8．……………………….8分 ‎16．解： S=x（30﹣x）……………………………….4分 自变量x的取值范围为：0＜x＜30．…………………8分 ‎　四、解答题（共2小题，每小题8分，满分16分）‎ ‎17．解：(1)y＝(x2－2x＋1)－4‎ ‎＝(x－1)2－4； 4分 ‎(2)令y＝0，得x2－2x－3＝0， ‎ 解得x1＝3，x2＝－1， ‎ 函数图象与x轴的交点坐标为(3，0)，(－1，0)．………8分 ‎18解：(1)△AB1C1，△A1B2C2如图所示； 4分 ‎(2)B1(－2，－3)，C2(3，1)； 8分 ‎　五、解答题（共2小题，每小题10分，满分20分）‎ ‎19． 解：（1）∵方程有两个实数根， ∴△≥0，‎ ‎∴9﹣4×1×（m﹣1）≥0，‎ 解得m≤；……………………………………..5分 ‎（2）∵x1+x2=﹣3，x1x2=m﹣1，‎ 又∵2（x1+x2）+x1x2+10=0，‎ ‎∴2×（﹣3）+m﹣1+10=0，‎ ‎∴m=﹣3．…………………………………………10分 ‎20． 解：（1）当1≤x＜50时，y=（200﹣2x）（x+40﹣30）=﹣2x2+180x+2000，‎ 当50≤x≤90时，‎ y=（200﹣2x）（90﹣30）=﹣120x+12000，‎ 综上所述：y=；………………………..5分 ‎（2）当1≤x＜50时，二次函数开口向下，二次函数对称轴为x=45，‎ 当x=45时，y最大=﹣2×452+180×45+2000=6050，‎ 当50≤x≤90时，y随x的增大而减小，‎ 当x=50时，y最大=6000，‎ 综上所述，该商品第45天时，当天销售利润最大，最大利润是6050元。……..10分 六、解答题（共2小题，每小题12分，满分24分）[来源:学_科_网Z_X_X_K]‎ ‎21． 证明：∵∠DAC与∠DBC是同弧所对的圆周角，‎ ‎∴∠DAC=∠DBC．‎ ‎∵AD平分∠CAE，‎ ‎∴∠EAD=∠DAC，‎ ‎∴∠EAD=∠DBC．…………………………………6分 ‎∵四边形ABCD内接于⊙O，‎ ‎∴∠EAD=∠BCD，‎ ‎∴∠DBC=∠DCB，‎ ‎∴DB=DC．………………………………………..12分 ‎22． 解：（1）∵抛物线的顶点为A（1，4），‎ ‎∴设抛物线的解析式y=a（x﹣1）2+4，‎ 把点B（0，3）代入得，a+4=3， 解得a=﹣1，‎ ‎∴抛物线的解析式为y=﹣（x﹣1）2+4；………………………………..4分 ‎（2）由（1）知，抛物线的解析式为y=﹣（x﹣1）2+4；‎ 令y=0，则0=﹣（x﹣1）2+4，‎ ‎∴x=﹣1或x=3，‎ ‎∴C（﹣1，0），D（3，0）；‎ ‎∴CD=4，‎ ‎∴S△BCD=CD×|yB|=×4×3=6；………………………………8分 ‎（3）由（2）知，S△BCD=CD×|yB|=×4×3=6；CD=4，‎ ‎∵S△PCD=S△BCD，[来源:Z.xx.k.Com]‎ ‎∴S△PCD=CD×|yP|=×4×|yP|=3，‎ ‎∴|yP|=，‎ ‎∵点P在x轴上方的抛物线上，‎ ‎∴yP＞0，‎ ‎∴yP=，‎ ‎∵抛物线的解析式为y=﹣（x﹣1）2+4；‎ ‎∴=﹣（x﹣1）2+4，‎ ‎∴x=1±，‎ ‎∴P（1+，），或P（1﹣，）．………………………..12分 ‎　七、解答题（共1小题，满分14分）‎ ‎23. 解：（1）∵△ADE绕点A按顺时针方向旋转，使AD、AB重合，得到△ABF，‎ ‎∵DE=BF，∠AFB=∠AED．‎ 故答案为：BF，AED；…………………………………………4分 ‎（2）将△ADQ绕点A按顺时针方向旋转90°，则AD与AB重合，得到△ABE，如图2，‎ 则∠D=∠ABE=90°，‎ 即点E、B、P共线，∠EAQ=∠BAD=90°，AE=AQ，BE=DQ，‎ ‎∵∠PAQ=45°，‎ ‎∴∠PAE=45°，‎ ‎∴∠PAQ=∠PAE，‎ 在△APE和△APQ中 ‎∵，‎ ‎∴△APE≌△APQ（SAS），‎ ‎∴PE=PQ，‎ 而PE=PB+BE=PB+DQ，‎ ‎∴DQ+BP=PQ；…………………………………9分 ‎（3）∵四边形ABCD为正方形，[来源:学科网ZXXK]‎ ‎∴∠ABD=∠ADB=45°，[来源:Zxxk.Com]‎ 如图，将△ADN绕点A按顺时针方向旋转90°，则AD与AB重合，得到△ABK，‎ 则∠ABK=∠ADN=45°，BK=DN，AK=AN，‎ 与（2）一样可证明△AMN≌△AMK，得到MN=MK，‎ ‎∵∠MBA+∠KBA=45°+45°=90°，‎ ‎∴△BMK为直角三角形，‎ ‎∴BK2+BM2=MK2，‎ ‎∴BM2+DN2=MN2．…………………………….14分 ‎…‎